
已知函数 .
.
(Ⅰ)若 ,求
,求 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的极值点.
的极值点.
(Ⅰ)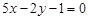 ;(Ⅱ)当
;(Ⅱ)当 时,
时, 的极小值点为
的极小值点为 和
和 ,极大值点为
,极大值点为 ;当
;当 时,
时, 的极小值点为
的极小值点为 ;当
;当 时,
时, 的极小值点为
的极小值点为 .
.
解析试题分析:(Ⅰ) 时,
时, ,先求切线斜率
,先求切线斜率
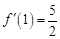 ,又切点为
,又切点为 ,利用直线的点斜式方程求出直线方程;(Ⅱ)极值点即定义域内导数为0的根,且在其两侧导数值异号,首先求得定义域为
,利用直线的点斜式方程求出直线方程;(Ⅱ)极值点即定义域内导数为0的根,且在其两侧导数值异号,首先求得定义域为 ,再去绝对号,分为
,再去绝对号,分为 和
和 两种情况,其次分别求
两种情况,其次分别求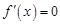 的根并与定义域比较,将定义域外的舍去,并结合图象判断其两侧导数符号,进而求极值点;
的根并与定义域比较,将定义域外的舍去,并结合图象判断其两侧导数符号,进而求极值点;
试题解析: 的定义域为
的定义域为 .
.
(Ⅰ)若 ,则
,则 ,此时
,此时 .因为
.因为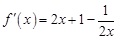 ,所以
,所以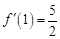 ,所以切线方程为
,所以切线方程为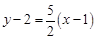 ,即
,即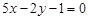 .
.
(Ⅱ)由于 ,
, .
.
⑴ 当 时,
时, ,
, ,
,
令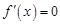 ,得
,得 ,
, (舍去),
(舍去),
且当 时,
时, ;当
;当 时,
时, ,
,
所以 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增, 的极小值点为
的极小值点为 .
.
⑵ 当 时,
时, .
.
① 当 时,
时, ,令
,令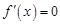 ,得
,得 ,
, (舍去).
(舍去).
若 ,即
,即 ,则
,则 ,所以
,所以 在
在 上单调递增;
上单调递增;
若 ,即
,即 , 则当
, 则当 时,
时, ;当
;当 时,
时, ,所以
,所以 在区间
在区间 上是单调递减,在
上是单调递减,在 上单调递增,
上单调递增, 的极小值点为
的极小值点为 .
.
② 当 时,
时, .
.
令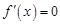 ,得
,得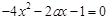 ,记
,记 ,
,
若 ,即
,即 时,
时, ,所以
,所以 在
在 上单调递减;
上单调递减;
若 ,即
,即 时,则由
时,则由

科目:高中数学 来源: 题型:解答题
学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.
(Ⅰ)求水面宽;
(Ⅱ)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?
(Ⅲ)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, .
.
(1)若 ,则
,则 ,
, 满足什么条件时,曲线
满足什么条件时,曲线 与
与 在
在 处总有相同的切线?
处总有相同的切线?
(2)当 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(3)当 时,若
时,若 对任意的
对任意的 恒成立,求
恒成立,求 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, ,
, ,其中
,其中 ,且
,且 .
.
⑴当 时,求函数
时,求函数 的最大值;
的最大值;
⑵求函数 的单调区间;
的单调区间;
⑶设函数 若对任意给定的非零实数
若对任意给定的非零实数 ,存在非零实数
,存在非零实数 (
( ),使得
),使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
(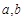 为常数),其图象是曲线
为常数),其图象是曲线 .
.
(1)当 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(2)设函数 的导函数为
的导函数为 ,若存在唯一的实数
,若存在唯一的实数 ,使得
,使得 与
与 同时成立,求实数
同时成立,求实数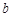 的取值范围;
的取值范围;
(3)已知点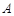 为曲线
为曲线 上的动点,在点
上的动点,在点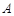 处作曲线
处作曲线 的切线
的切线 与曲线
与曲线 交于另一点
交于另一点 ,在点
,在点 处作曲线
处作曲线 的切线
的切线 ,设切线
,设切线 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得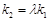 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区注重生态环境建设,每年用于改造生态环境总费用为 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用 随每年改造生态环境总费用
随每年改造生态环境总费用 增加而增加;②每年改造生态环境总费用至少
增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用 不得低于每年改造生态环境总费用
不得低于每年改造生态环境总费用 的15%,但不得高于每年改造生态环境总费用
的15%,但不得高于每年改造生态环境总费用 的25%.
的25%.
若 ,
, ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=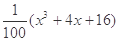 作为生态环境改造投资方案.
作为生态环境改造投资方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com