
高考数学复习易做易错题选
不等式部分
一、选择题:
1.(如中)设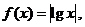 若0<a<b<c,且f(a)>f(b)>f(c),则下列结论中正确的是
若0<a<b<c,且f(a)>f(b)>f(c),则下列结论中正确的是
A (a-1)(c-1)>0 B
ac>
错解原因是没有数形结合意识,正解是作出函数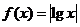 的图象,由图可得出选D.
的图象,由图可得出选D.
2.(如中)设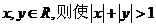 成立的充分不必要条件是
成立的充分不必要条件是
A 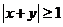 B
B 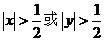 C
C 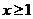 D x<-1
D x<-1
错解:选B,对充分不必要条件的概念理解不清,“或”与“且”概念不清,正确答案为D。
3.(如中)不等式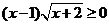 的解集是
的解集是
A  B
B 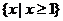 C
C 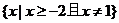 D
D 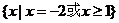
错解:选B,不等式的等价转化出现错误,没考虑x=-2的情形。正确答案为D。
4.(如中)某工厂第一年的产量为A,第二年的增长率为a,第三年的增长率为b,这两年的平均增长率为x,则
A  B
B 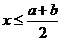 C
C 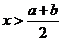 D
D 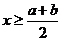
错解:对概念理解不清,不能灵活运用平均数的关系。正确答案为B。
5.(如中)已知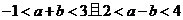 ,则
,则
A 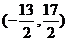 B
B 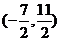 C
C 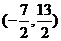 D
D 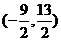
错解:对条件“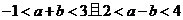 ”不是等价转化,解出a,b的范围,再求
”不是等价转化,解出a,b的范围,再求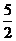 (a+b)
(a+b)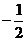 (a-b),求出结果为D。
(a-b),求出结果为D。
6.(石庄中学)若不等式ax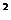 +x+a<0的解集为 Φ,则实数a的取值范围( )
+x+a<0的解集为 Φ,则实数a的取值范围( )
A a≤-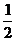 或a≥
或a≥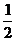 B a<
B a<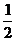 C -
C -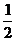 ≤a≤
≤a≤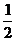 D a≥
D a≥ 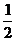
正确答案:D 错因:学生对一元二次不等式与二次函数的图象之间的关系还不能掌握。
7.(石庄中学)已知函数y=┯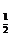 (3x
(3x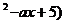 在[-1,+∞)上是减函数,则实数a的取值范围( )
在[-1,+∞)上是减函数,则实数a的取值范围( )
A a≤-6 B -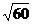 <a<
<a< -8≤a≤-6
-8≤a≤-6
正确答案:C 错因:学生忘记考虑定义域真数大于0这一隐含条件。
8.(石庄中学)已知实数x、y、z满足x+y+z=0,xyz>0记T=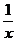 +
+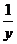 +
+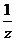 ,则( )
,则( )
A T>0 B T=
正确答案: C 错因:学生对已知条件不能综合考虑,判断T的符号改为判定 xyz(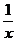 +
+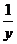 +
+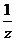 )的符号。
)的符号。
9.(石庄中学)下列四组条件中,甲是乙的充分不必要条件的是( )
A. 甲 a>b,乙
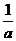 <
< B 甲 ab<0,乙
ㄏa+bㄏ<ㄏa-bㄏ
C
甲 a=b ,
B 甲 ab<0,乙
ㄏa+bㄏ<ㄏa-bㄏ
C
甲 a=b , 乙 a+b=2
乙 a+b=2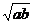 D 甲
D 甲 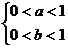 ,乙
,乙 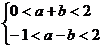
正确答案: D 错因:学生对不等式基本性质成立的条件理解不深刻。
10.(石庄中学)f(x)=?2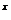 ―1|,当a<b<c时有f(a)>f(c)>f(b)则( )
A
a<0,b<0,c<0 B a<0,b>0,c>
―1|,当a<b<c时有f(a)>f(c)>f(b)则( )
A
a<0,b<0,c<0 B a<0,b>0,c>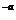 <2
<2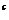 D 2
D 2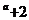
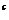 <2
<2
正确答案:D 错因:学生不能应用数形结合的思想方法解题。
11.(磨中)a,b∈R,且a>b,则下列不等式中恒成立的是( )
A.a2>b2 B.( 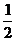 ) a <(
) a <(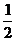 )b C.lg(a-b)>0 D.
)b C.lg(a-b)>0 D.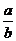 >1
>1
正确答案:B。
错误原因:容易忽视不等式成立的条件。
12.(磨中)x为实数,不等式|x-3|-|x-1|>m恒成立,则m的取值范围是( )
A.m>2 B.m<
正确答案:D。
错误原因:容易忽视绝对值的几何意义,用常规解法又容易出错。
13.(磨中)已知实数x、y满足x2+y2=1,则(1-xy)(1+xy)( )
A.有最小值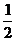 ,也有最大值1 B.有最小值
,也有最大值1 B.有最小值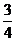 ,也有最大值1
,也有最大值1
C.有最小值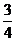 ,但无最大值 D.有最大值1,但无最小值
,但无最大值 D.有最大值1,但无最小值
正确答案:B 。
错误原因:容易忽视x、y本身的范围。
14.(磨中)若a>b>0,且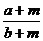 >
>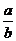 ,则m的取值范围是( )
,则m的取值范围是( )
A. m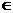 R B.
m>0 C. m<0 D. ?b<m<0
R B.
m>0 C. m<0 D. ?b<m<0
正确答案:D 。
错误原因:错用分数的性质。
15.(城西中学)已知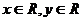 ,则
,则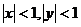 是
是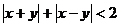 的( )条件
的( )条件
A、充分不必要 B、必要不充分 C、既不充分也不必要 D、充要
正确答案:D
错因:不严格证明随便判断。
16.(城西中学)如果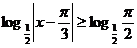 那么
那么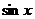 的取值范围是( )
的取值范围是( )
A、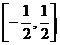 B、
B、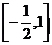 C、
C、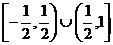 D、
D、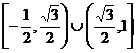
正确答案:B
错因:利用真数大于零得x不等于60度,从而正弦值就不等于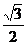 ,于是就选了D.其实x等于120度时可取得该值。故选B。
,于是就选了D.其实x等于120度时可取得该值。故选B。
17.(一中)设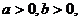 则以下不等式中不恒成立的是
( )
则以下不等式中不恒成立的是
( )
A.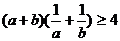 B.
B.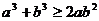
C.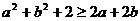 D.
D.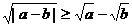

正确答案:B
18.(一中)如果不等式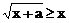 (a>0)的解集为{x|m≤x≤n},且|m-n|=2a,则a的值等于( )
(a>0)的解集为{x|m≤x≤n},且|m-n|=2a,则a的值等于( )
A.1 B.2 C.3 D.4
正确答案:B
19.(蒲中)若实数m,n,x,y满足m2+n2=a,x2+y2=b(a≠b),则mx+ny的最大值为( )
A、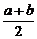 B、
B、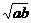 C、
C、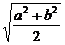 D、
D、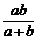
答案:B
点评:易误选A,忽略运用基本不等式“=”成立的条件。
20.(蒲中)数列{an}的通项式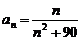 ,则数列{an}中的最大项是( )
,则数列{an}中的最大项是( )
A、第9项 B、第8项和第9项
C、第10项 D、第9项和第10项
答案:D
点评:易误选A,运用基本不等式,求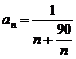 ,忽略定义域N*。
,忽略定义域N*。
21.(丁中).若不等式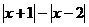 >
>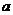 在
在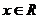 上有解,则
上有解,则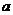 的取值范围是
( )
的取值范围是
( )
A. 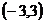 B.
B.
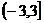 C.
C. 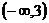 D.
D.
错解:D
错因:选D恒成立。
正解:C
22.(薛中)已知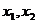 是方程
是方程 的两个实根,则
的两个实根,则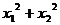 的最大值为( )
的最大值为( )
A、18 B、19 C、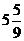 D、不存在
D、不存在
答案:A
错选:B
错因: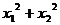 化简后是关于k的二次函数,它的最值依赖于
化简后是关于k的二次函数,它的最值依赖于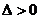 所得的k的范围。
所得的k的范围。
23.(薛中)实数m,n,x,y满足m2+n2=a , x2+y2=a , 则mx+ny的最大值是 。
A、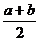 B、
B、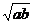 C、
C、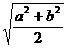 D、
D、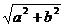
答案:B
错解:A
错因:忽视基本不等式使用的条件,而用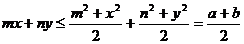 得出错解。
得出错解。
24.(案中)如果方程(x-1)(x 2-2x+m)=0的三个根可以作为一个三角形的三条边长,那么实数m的取值范围是 ( )
A、0≤m≤1
B、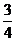 <m≤1 C、
<m≤1 C、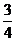 ≤m≤1 D、m≥
≤m≤1 D、m≥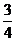
正确答案:(B)
错误原因:不能充分挖掘题中隐含条件。
二填空题:
1.(如中)设 ,则
,则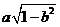 的最大值为
的最大值为
错解:有消元意识,但没注意到元的范围。正解:由 得:
得: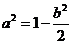 ,且
,且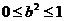 ,原式=
,原式=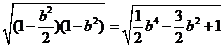 ,求出最大值为1。
,求出最大值为1。
2.(如中)若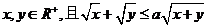 恒成立,则a的最小值是
恒成立,则a的最小值是
错解:不能灵活运用平均数的关系,正解:由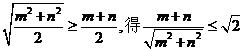 ,即
,即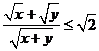 ,故a的最小值是
,故a的最小值是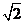 。
。
3.(如中)已知两正数x,y 满足x+y=1,则z=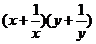 的最小值为
。
的最小值为
。
错解二、
 ,所以z的最小值是
,所以z的最小值是 。
。
错解分析:解一等号成立的条件是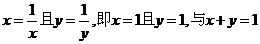 相矛盾。解二等号成立的条件是
相矛盾。解二等号成立的条件是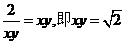 ,与
,与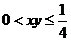 相矛盾。
相矛盾。
正解:z=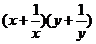 =
=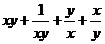 =
=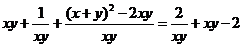 ,令t=xy, 则
,令t=xy, 则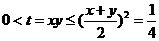 ,由
,由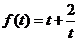 在
在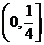 上单调递减,故当t=
上单调递减,故当t=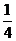 时
时 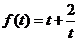 有最小值
有最小值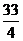 ,所以当
,所以当 时z有最小值
时z有最小值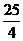 。
。
4.(磨中)若对于任意x∈R,都有(m-2)x2-2(m-2)x-4<0恒成立,则实数m的取值范围是 。
正确答案:(-2,2) 。
错误原因:容易忽视m=2。
5.(城西中学)不等式ax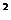 + bx + c>0 ,解集区间(-
+ bx + c>0 ,解集区间(- 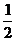 ,2),对于系数a、b、c,则有如下结论:
,2),对于系数a、b、c,则有如下结论:
① a >0 ②b>0 ③ c>0 ④a + b + c>0 ⑤a ? b + c>0,其中正确的结论的序号是________________________________.
正确答案 2 、3、 4
错因:一元二次函数的理解
6.(一中)不等式(x-2)≥0的解集是 .
正确答案: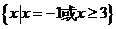
7.(一中)不等式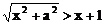 的解集为(-∞,0),则实数a的取值范围是_____________________。
的解集为(-∞,0),则实数a的取值范围是_____________________。
正确答案:{-1,1}
8.(一中)若α,β,γ为奇函数f(x)的自变量,又f(x)是在(-∞,0)上的减函数,且有α+β>0,α+γ>0,β+γ>0,则f(α)+f(β)与f(-γ)的大小关系是:f(α)+f(β) ______________f(-γ)。正确答案:<
9.(蒲中)不等式|x+1|(2x-1)≥0的解集为____________
答案: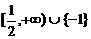
点评:误填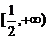 而忽略x=-1。
而忽略x=-1。
10.(蒲中)设x>1,则y=x+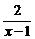 的最小值为___________
的最小值为___________
答案: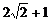
点评:误填:4,错因: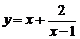 ≥
≥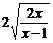 ,当且仅当
,当且仅当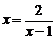 即x=2时等号成
即x=2时等号成
立,忽略了运用基本不等式求最值时的“一正、二定、三相等”的条件。
11.(丁中)设实数a,b,x,y满足a2+b2=1,x2+y2=3, 则ax+by的取值范围为_______________.
错解: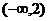
错因: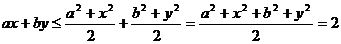 ,当且仅当
,当且仅当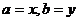 时等号成立,而此时
时等号成立,而此时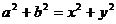 与已知条件矛盾。
与已知条件矛盾。
正解:[-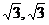 ]
]
12.(丁中).-4<k<o是函数y=kx2-kx-1恒为负值的___________条件
错解:充要条件
错因:忽视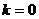 时
时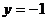 符合题意。
符合题意。
正解:充分非必要条件
13.(丁中)函数y=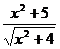 的最小值为_______________
的最小值为_______________
错解:2
错因:可化得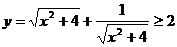 ,而些时等号不能成立。
,而些时等号不能成立。
正解: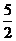
14.(丁中)已知a,b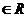 ,且满足a+3b=1,则ab的最大值为___________________.
,且满足a+3b=1,则ab的最大值为___________________.
错解:
错因:由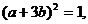 得
得 ,
,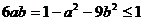 ,
,
等号成立的条件是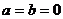 与已知矛盾。
与已知矛盾。
正解: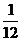
15.(薛中)设函数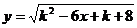 的定义域为R,则k的取值范围是
。
的定义域为R,则k的取值范围是
。
A、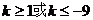 B、
B、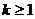 C、
C、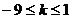 D、
D、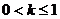
答案:B
错解:C
错因:对二次函数图象与判别式的关系认识不清,误用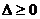 。
。
16.(薛中)不等式(x-2)2
(3-x) (x-4)3 (x-1) 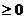 的解集为
。
的解集为
。
答案: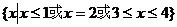
错解: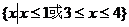
错因:忽视x=2时不等式成立。
17.(薛中)已知实数x,y满足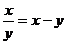 ,则x的取值范围是 。
,则x的取值范围是 。
答案: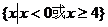
错解: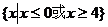
错因:将方程作变形使用判别式,忽视隐含条件“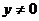 ”。
”。
18.(薛中)若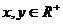 ,且2x+8y-xy=0则x+y的范围是
。
,且2x+8y-xy=0则x+y的范围是
。
答案: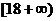 由原方程可得
由原方程可得
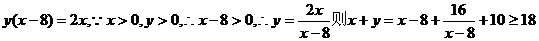 错解:
错解: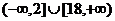 设
设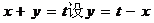 代入原方程使用判别式。
代入原方程使用判别式。
错因:忽视隐含条件,原方程可得y (x-8)=2x,则x>8则x+y>8
19.(案中)已知实数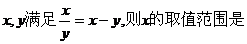 。
。
正确答案: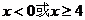
错误原因:找不到解题思路,另外变形为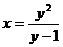 时易忽视
时易忽视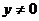 这一条件。
这一条件。
20.(案中)已知两个正变量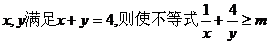 恒成立的实数m的取值范围是
。
恒成立的实数m的取值范围是
。
正确答案: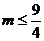
错误原因:条件x+y=4不知如何使用。
21.(案中)已知函数①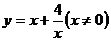 ②
②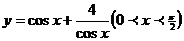 ③
③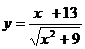 ④
④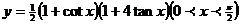 ,其中以4为最小值的函数个数是
。
,其中以4为最小值的函数个数是
。
正确答案:0
错误原因:对使用算术平均数和几何平均数的条件意识性不强。
22.(案中)已知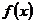 是定义在
是定义在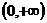 的等调递增函数,
的等调递增函数,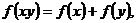 且
且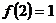 ,则不等式
,则不等式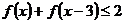 的解集为
。
的解集为
。
正确答案: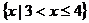
错误原因:不能正确转化为不等式组。
23.(案中)已知a2+b2+c2=1, x2+y2+z2=9, 则ax+by+cz的最大值为
正确答案:3
错误原因:忽视使用基本不等式时等号成立的条件,易填成5。应使用如下做法: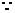 9a2+x2≥6ax, 9b2+y2 ≥6by,9c2+z2≥6cz,
9a2+x2≥6ax, 9b2+y2 ≥6by,9c2+z2≥6cz,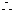 6(ax+by+cz)≤9(a2+b2+c2)+9(x2+y2+z2)
= 18,
6(ax+by+cz)≤9(a2+b2+c2)+9(x2+y2+z2)
= 18, 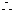 ax+by+cz≤3
ax+by+cz≤3
三、解答题:
1.(如中)是否存在常数 c,使得不等式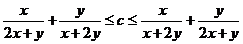 对任意正数 x,y恒成立?
对任意正数 x,y恒成立?
错解:证明不等式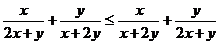 恒成立,故说明c存在。
恒成立,故说明c存在。
正解:令x=y得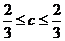 ,故猜想c=
,故猜想c=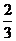 ,下证不等式
,下证不等式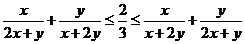 恒成立。
恒成立。
要证不等式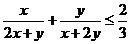 ,因为x,y是正数,即证3x(x+2y)+3y(2x+y)≤2(2 x+y)(x+2y),也即证
,因为x,y是正数,即证3x(x+2y)+3y(2x+y)≤2(2 x+y)(x+2y),也即证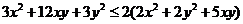 ,即2xy≤
,即2xy≤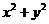 ,而此不等式恒成立,同理不等式
,而此不等式恒成立,同理不等式 也成立,故存在c=
也成立,故存在c=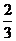 使原不等式恒成立。
使原不等式恒成立。
2.(如中)已知适合不等式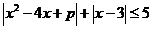 的x的最大值为3,求p的值。
的x的最大值为3,求p的值。
错解:对此不等式无法进行等价转化,不理解“x的最大值为3”的含义。
正解:因为x的最大值为3,故x-3<0,原不等式等价于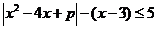 ,
,
即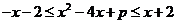 ,则
,则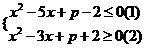
 ,
,
设(1)(2)的根分别为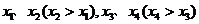 ,则
,则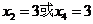
若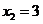 ,则9-15+p-2=0,p=8
,则9-15+p-2=0,p=8
若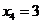 ,则9-9+p+2=0,p=-2
,则9-9+p+2=0,p=-2
当a=-2时,原方程组无解,则p=8
3.(搬中) 设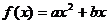 ,且
,且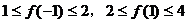 ,求
,求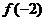 的取值范围。
的取值范围。
解:令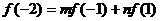
则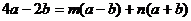
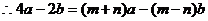
比较系数有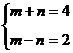
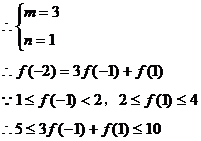
即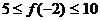
说明:此题极易由已知二不等式求出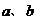 的范围,然后再求
的范围,然后再求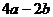 即
即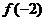 的范围,这种解法错在已知二不等式中的等号成立的条件不一定相同,它们表示的区域也不一定相同,用待定系数法则容易避免上述错误。
的范围,这种解法错在已知二不等式中的等号成立的条件不一定相同,它们表示的区域也不一定相同,用待定系数法则容易避免上述错误。
4.(搬中) 若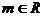 ,解关于
,解关于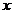 的不等式:
的不等式: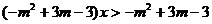 。
。
解:令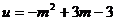
则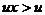
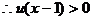
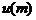 的判别式
的判别式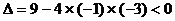
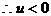 恒成立
恒成立
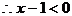
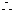 原不等式的解为
原不等式的解为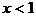
说明:此题容易由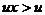 得出
得出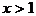 的错误结论。解有关不等式的问题,一定要注意含参数的表达式的符号,否则易出错误。
的错误结论。解有关不等式的问题,一定要注意含参数的表达式的符号,否则易出错误。
5.(搬中) 求函数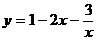 的极大值或极小值。
的极大值或极小值。
解:当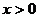 时,
时,
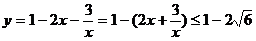
当且仅当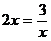
即 时,
时,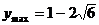
当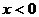 时,
时,
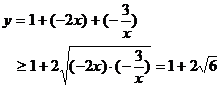
当且仅当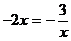
即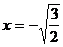 时,
时,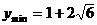
说明:此题容易漏掉对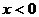 的讨论。不等式
的讨论。不等式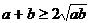 成立的前提是
成立的前提是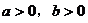 。
。
6.(搬中)求函数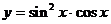 的最大值。
的最大值。
解: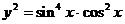
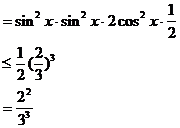
当且仅当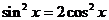
即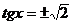 时,
时,
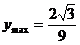
说明:此题容易这样做: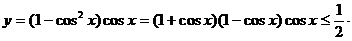
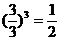 。但此时等号应满足条件
。但此时等号应满足条件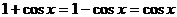 ,这样的
,这样的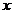 是不存在的,错误的原因是没有考虑到等号成立的条件。这一点在运用重要不等式时一定要引起我们高度的重视。
是不存在的,错误的原因是没有考虑到等号成立的条件。这一点在运用重要不等式时一定要引起我们高度的重视。
7.(搬中)解不等式: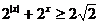 。
。
解:当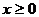 时,原不等式为
时,原不等式为
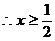
当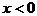 时,原不等式为
时,原不等式为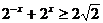
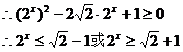
又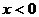
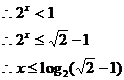
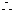 原不等式的解为
原不等式的解为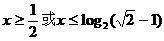
说明:此题易在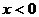 时
时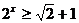 处出错,忽略了
处出错,忽略了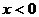 的前提。这提醒我们分段求解的结果要考虑分段的前提。
的前提。这提醒我们分段求解的结果要考虑分段的前提。
7.(搬中) 若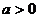 且
且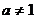 ,解不等式:
,解不等式:
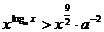
解:若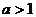 ,两边取以
,两边取以 为底的对数
为底的对数
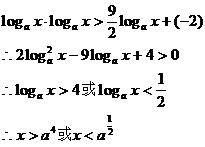
若 ,同样有,
,同样有,
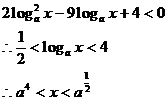
又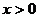
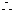 当
当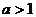 时不等式的解为
时不等式的解为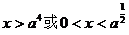
当 时不等式的解为
时不等式的解为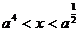
说明:此题易在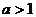 时的解中出错,容易忽略
时的解中出错,容易忽略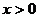 这个条件。解决对数问题要注意真数大于0的条件。
这个条件。解决对数问题要注意真数大于0的条件。
8.(搬中)方程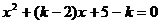 的两根都大于2,求实数
的两根都大于2,求实数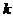 的取值范围。
的取值范围。
解:设方程的两根为 ,则必有
,则必有
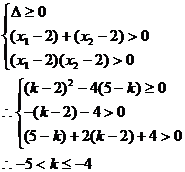
说明:此题易犯这样的错误:
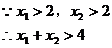
且
和判别式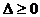 联立即得
联立即得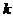 的范围
的范围
原因是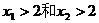 只是
只是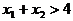 的充分条件
的充分条件
即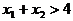 不能保证
不能保证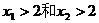 同时成立
同时成立
9.(磨中)设函数f(x)=logb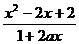 (b>0且b≠1),
(b>0且b≠1),
(1)求f(x)的定义域;
(2)当b>1时,求使f(x)>0的所有x的值。
解 (1)∵x2-2x+2恒正,
∴f(x)的定义域是1+2ax>0,
即当a=0时,f(x)定义域是全体实数。
当a>0时,f(x)的定义域是(-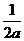 ,+∞)
,+∞)
当a<0时,f(x)的定义域是(-∞,-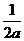 )
)
(2)当b>1时,在f(x)的定义域内,f(x)>0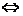
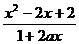 >1
>1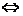 x2-2x+2>1+2ax
x2-2x+2>1+2ax
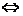 x2-2(1+a)x+1>0
x2-2(1+a)x+1>0
其判别式Δ=4(1+a)2-4=4a(a+2)
(i)当Δ<0时,即-2<a<0时
∵x2-2(1+a)x+1>0
∴f(x)>0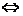 x<-
x<-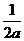
(ii)当Δ=0时,即a=-2或0时
若a=0,f(x)>0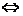 (x-1)2>0
(x-1)2>0
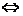 x∈R且x≠1
x∈R且x≠1
若a=-2,f(x)>0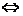 (x+1)2>0
(x+1)2>0
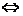 x<
x<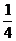 且x≠-1
且x≠-1
(iii)当△>0时,即a>0或a<-2时
方程x2-2(1+a)x+1=0的两根为
x1=1+a-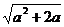 ,x2=1+a+
,x2=1+a+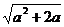
若a>0,则x2>x1>0>-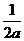
∴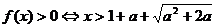 或
或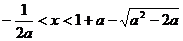
若a<-2,则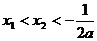
∴f(x)>0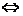 x<1+a-
x<1+a-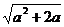 或1+a+
或1+a+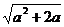 <x<-
<x<-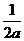
综上所述:当-2<a<0时,x的取值集合为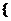 x|x<-
x|x<-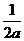
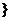
当a=0时,x∈R且x≠1,x∈R,当a=-2时: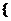 x|x<-1或-1<x<
x|x<-1或-1<x<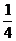
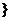
当a>0时,x∈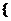 x|x>1+a+
x|x>1+a+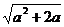 或-
或-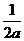 <x<1+a-
<x<1+a-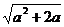
当a<-2时,x∈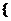 x|x<1+a-
x|x<1+a-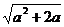 或1+a+
或1+a+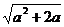 <x<-
<x<-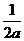
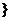
错误原因:解题时易忽视函数的定义域,不会合理分类。
10.(城西中学)设集合M=[-1,1],N=[-,],f(x)=2x2+mx-1,若x∈N,m∈M,求证|f(x)|≤
证明:|f(x)|=|2x2+mx-1|= |(2x2-1)+mx|≤|(2x2-1)|+|mx|= (2x2-1)+|mx|≤(2x 2-1)+| x|
=-2(| x|-)2+≤
错因:不知何时使用绝对值不等式。
11.(城西中学)在边长为a的正三角形中,点P、Q、R分别在BC、CA、AB上,且BP+CQ+AR=a,设BP=x,CQ=y,AR=z,三角形PQR的面积为s,求s的最大值及相应的x、y、z的值。
解 设ΔBPR、ΔPCR、ΔARQ的面积为s1、、s2、s3,则
S=SΔABC-S1-S2-S3=a2-[a2-(xy+xz+yz)]=(xy+xz+yz)
由x+y+z=a,得xy+yz+zx≤,∴Smav=a2,此时,x=y=z=
错因:不知如何使用基本不等式。
12.(蒲中)设a、b∈R,求证: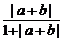 ≤
≤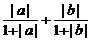
证明:当|a+b|=0时,不等式已成立
当|a+b|≠0时,∵ |a+b|≤|a|+|b|
∴ 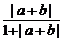 =
=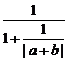 ≤
≤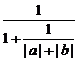 =
=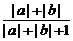
=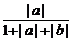 +
+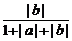 ≤
≤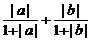
点评:错证:∵|a+b|≤|a|+|b|
∴ 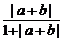 ≤
≤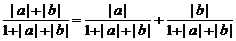 ≤
≤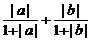 ①
①
错因:①的推理无根据。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com