辽宁省部分重点中学协作体2009年高考模拟考试
数学试题(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。考试时间120分钟。
参考公式:
如果事件A、B互斥,那么
球的表面积公式
P(A+B)=P(A)+P(B)

如果事件A、B相互独立,那么 其中R表示球的半径
P(A?B)=P(A)?P(B) 球的体积公式
如果事件A在一次试验中发生 
的概率是P,那么n次独立重复
其中R表示球的半径
试验中A恰好发生k次的概率


第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.抛物线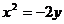 的准线方程是 ( )
的准线方程是 ( )
试题详情
试题详情
2.设复数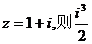 等于 ( )
等于 ( )
试题详情
试题详情
3.在直线AB上,点A的坐标是(1,2),向量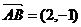 ,则直线AB的方程为( )
,则直线AB的方程为( )
试题详情
A.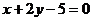 B.
B.
试题详情
C.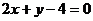 D.
D.
试题详情
4.已知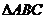 的三个内角A、B、C所对的边分别为
的三个内角A、B、C所对的边分别为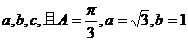 ,则角B等于 ( )
,则角B等于 ( )
试题详情
试题详情
|
试题详情
A.若 试题详情
B.若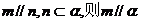 试题详情
C.若 试题详情
D.若 试题详情
试题详情
的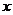 所有可能取值的和等于
( ) 所有可能取值的和等于
( ) A.0 B.1 C.2 D.3 试题详情
7.已知幂函数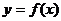 的图象经过点 的图象经过点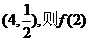 = ( ) = ( ) 试题详情
试题详情
8.已知正项等比数列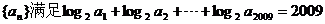 ,则 ,则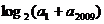 的最小值为 ( ) 的最小值为 ( ) 试题详情
A.1 B. C.2 D. C.2 D. 试题详情
9.已知函数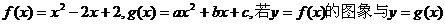 的图象关于点(2,0)对称,则 的图象关于点(2,0)对称,则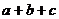 等于 ( ) 等于 ( ) A.5 B.-5 C.1 D.-1 试题详情
10.现有六名学生站成一排照相,其中甲、乙两人不能相邻,丙、丁两人也不能相邻,则不同的站排方法共有 ( ) A.408种 B.336种 C.264种 D.240种 试题详情
试题详情
A.向左平移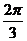 个单位 B.向右平移 个单位 B.向右平移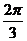 个单位 个单位 试题详情
C.向左平移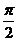 个单位 D.向右平移 个单位 D.向右平移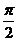 个单位 个单位
|
试题详情
A.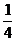 B. B.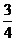 C. C.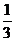 D. D. 第Ⅱ卷(非选择题
共90分) 本卷包括必答题和选答题两部分,第13题―第21题为必答题,每个试题考生都必须作答,第22题为选答题,考生根据要求作答。 试题详情
|
试题详情
13.一个几何体的三视图如图所示,主视图、左视图、俯视图 均为腰长为1的等腰直角三角形,则其外接球的表面积 为
。 试题详情
14.若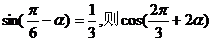 =
。 =
。 试题详情
15.已知双曲线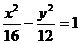 的左、右焦点分虽为F1、F2,过点 的左、右焦点分虽为F1、F2,过点 试题详情
F1作直线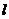 交双曲线的左支于A、B两点,且 交双曲线的左支于A、B两点,且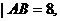 则三角形ABF2的周长等于
。 则三角形ABF2的周长等于
。 试题详情
16.已知在四面体A―BCD中,各棱长均为1,点E是线段BC的中点,则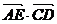 等于
。 等于
。 试题详情
三、解答题:本大题共6小题,满分70分,解答须写出文字说明,证明过程和演算步骤。 17.(本小题满分10)
20090514 (I)求n的值; (II)若从中不放回地逐一抽取,取到所有白球则停止抽取。在前3次取球中恰取到1个白球的条件下,共需取球Y次,求Y的分布列和E(Y)。
试题详情
试题详情
已知四棱锥P―ABCD的底面为直角梯形,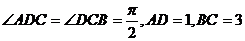 ,PC=CD=2, ,PC=CD=2,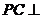 平面ABCD,E是线段AB的中点。 平面ABCD,E是线段AB的中点。 试题详情

(II)求二面角B―PA―C的大小。
试题详情
试题详情
已知数列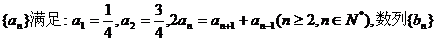 满足: 满足: 试题详情
(I)求证:数列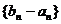 为等比数列; 为等比数列; 试题详情
(II)求证:数列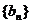 为递增数列; 为递增数列; 试题详情
(III)若当且仅当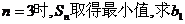 的取值范围。 的取值范围。
|
|
|
试题详情
20.(本小题满分12分)
|
试题详情
(I)当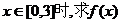 的值域; 的值域; 试题详情
(II)对于任意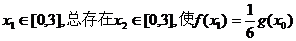 成立,求实数 成立,求实数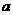 的取值范围。 的取值范围。 试题详情
试题详情
已知椭圆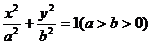 的长轴长为4,离心率为 的长轴长为4,离心率为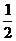 ,点P是椭圆上异于顶点的任意一点,过点P作椭圆的切线 ,点P是椭圆上异于顶点的任意一点,过点P作椭圆的切线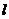 ,交y轴于点A,直线 ,交y轴于点A,直线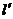 过点P且垂直于 过点P且垂直于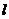 ,交 ,交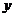 轴于点B。 轴于点B。 (I)求椭圆的方程; (II)试判断以AB为直径的圆能否经过定点?若能,求出定点坐标;若不能,请说明理由。 试题详情
22.请考生在A、B、C三题中选一题作答,如果多做,则按所做的第一题记分。 试题详情

选修4-1:几何证明选讲 如图,AB、CD是圆的两条平行弦,BE//AC, 并交CD于E,交圆于F,过A点的切线交DC的 延长线于P,PC=ED=1,PA=2。 (I)求AC的长; (II)求证:EF=BE。 B.(本小题满分10) 选修4-4:坐标系与参数方程
试题详情
已知直线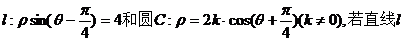 上的点到圆C上的点的最小距离等于2。 上的点到圆C上的点的最小距离等于2。 (I)求圆心C的直角坐标; (II)求实数k的值。 C.(本小题满分10分) 选修4-5:不等式选讲 试题详情
已知函数 试题详情
(I)求不等式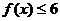 的解集; 的解集; 试题详情
(II)若关于x的不等式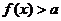 恒成立,求实数 恒成立,求实数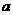 的取值范围。 的取值范围。 试题详情
一、选择题: DDABD ACCBB CD 二、填空题: 13. 14. 14. 15.32 16. 15.32 16.  三、解答题: 17.解:(I) 服从超几何分布 服从超几何分布   3分 3分 (II) 5分 5分  7分 7分  9分 9分 Y 5 6 7 P 


…………10分

18.解:(I)取CD中点F,连接EF, 则        4分 4分   平面PAC 6分 平面PAC 6分 (II)以点C为坐标原点,分别以CD,CB,CP为x轴,y轴,z轴建立空间直角坐标系 , , 则  平面PAC 平面PAC  8分
8分 设平面PAB的一个法向量为 , , 由 , , 得 不妨令 , , 即 10分 10分   12分
12分 19.解:(I)  是等差数列 是等差数列 又  2分 2分    5分
5分 又  为首项,以 为首项,以 为公比的等比数列
6分 为公比的等比数列
6分 (II)  当 又   是单调递增数列
9分 是单调递增数列
9分 (III) 时, 时,  即  12分 12分 20.解:(I) 
0 (0,1) 1 (1,3) 3 
+ 0 - 
0 
1 

 3分 3分 (II)设 时,函数 时,函数 的值域为A, 的值域为A,  , , 总存在   (1)当 时, 时,  上单调递减, 上单调递减,    6分 6分 (2)当 时, 时,  令  (舍去) (舍去) ①当 时,列表如下: 时,列表如下:  0 


3 
- 0 + 
0 



 若 若 , , 则  9分
9分 ②当 时, 时, 时, 时,  函数 函数 上单调递减 上单调递减    11分 11分 综上,实数 的取值范围是 的取值范围是 12分
12分 21.解:(I)   2分 2分 (II)设点 直线 的方程为 的方程为 代入 整理,得  是方程的两个相等实根 是方程的两个相等实根  解,得 6分 6分  令 ,得点A的坐标为 ,得点A的坐标为 又   又直线  令 ,得点B的坐标为 ,得点B的坐标为 8分
8分  整理,得 10分
10分 令  以AB为直径的圆恒过定点(1,0)和(-1,0)。 12分 以AB为直径的圆恒过定点(1,0)和(-1,0)。 12分 22.A.解:(I)  , , 又 3分
3分      7分 7分 (II)   10分 10分 B.解:(I)   2分 2分 即  4分
4分 (II)  6分 6分  即 8分 8分 两边平方,得  解,得 10分
10分 C.解:(I)原不等式等价于  或 3分 3分 解,得 即不等式的解集为 6分 6分 (II) 8分 8分  10分
10分
| | | | | | | | | | | | | | | | | |





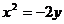 的准线方程是 ( )
的准线方程是 ( )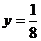 B.
B.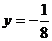 C.
C.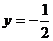 D.
D.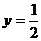
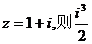 等于 ( )
等于 ( )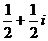 B.
B.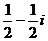 C.
C.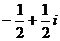 D.
D.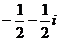
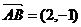 ,则直线AB的方程为( )
,则直线AB的方程为( )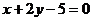 B.
B.
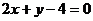 D.
D.
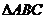 的三个内角A、B、C所对的边分别为
的三个内角A、B、C所对的边分别为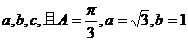 ,则角B等于 ( )
,则角B等于 ( )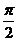 B.
B.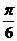 C.
C.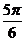 D.
D.