练习册

  • 练习册
  • 试题

    抚州一中2009届高三第四次模拟考试

    数学试卷（文）

     

    命题人 ：高三数学组　　　　　　　　　考试时间 ：2009.5

    第Ⅰ卷（选择题　共60分）

     

    一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

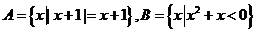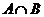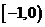
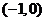
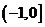
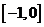
    1．设集合高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。等于　　　　（　　）

    试题详情

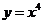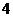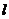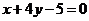
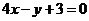
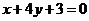
    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。            　高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。      高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。   　　高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。     　    　　高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    2．若曲线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的一条切线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的斜率为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则切线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的方程是　　　　　　　　（　　）

    试题详情

    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                             高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。   

    试题详情

    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                                  高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

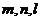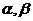    3．已知三条不重合的直线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，两个不重合的平面高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，有下列命题

    试题详情

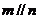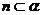
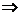
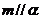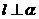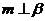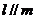
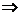
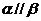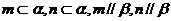
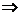
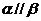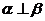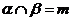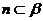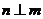
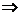
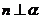    ①高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。；      ②高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。；

    试题详情

    ③高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。；

    试题详情

    ④高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。.

         其中正确的命题个数是　　　　　　　　　　　　　　　　　　　　　　　（　　）

    试题详情

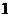
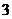
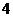
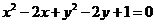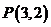    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                         高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                        高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                        高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    4．从圆高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。外一点高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。向这个圆作两条切线，则两切线夹角的余弦值为（ ）

    试题详情

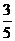
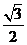
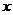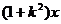
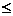
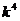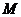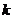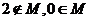
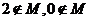
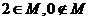
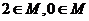
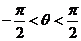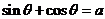    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。      　　　　高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                     高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

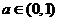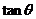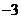
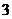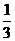
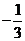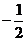
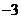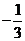
    5．若关于高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的不等式高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。＋4的解集是高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则对任意实常数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，总有（    ）

    试题详情

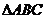    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                        高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                 

    试题详情

    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                                       高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    6．已知高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，且高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，其中高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的值有可能是（　　）

    试题详情

    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。　　　　高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。或高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。　　　　　高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。或高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。　　　　　高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。或高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

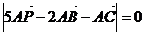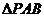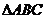    7．设高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。所在平面内一点，且高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的面积与高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 的面积之比为                                                    （    ）

    试题详情

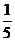
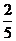
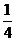
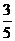
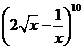    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 

    试题详情

    8．二项式高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。展开式中，所有有理项（不含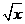高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的项）的系数之和为      （    ）

    试题详情

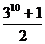
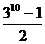
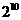
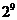
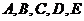           高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。           高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。             高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

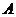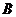    9．高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。五人争夺某项比赛的前三名，组织者对前三名发给不同的奖品，若高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。获奖，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。不是第一名，则不同的发奖方式共有                  （    ）

    试题详情

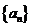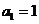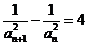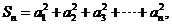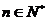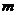             高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。72种                 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。30种                   高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。24种                   高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。14种

    试题详情

    10．数列高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。满足：高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。若高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    对于任意高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。都成立，则正整数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的最小值为( 　  )www.1010jiajiao.com

    　　　　　　　　　　　　　　　　　　　　　　　

    试题详情

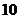
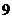
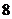
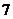
    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                 　高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。          　高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。               高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

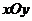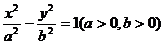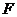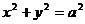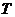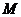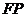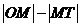    11．在直角坐标系高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。中，过双曲线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的左焦点高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。作圆高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的一条切线（切点为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。）交双曲线右支于点高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，若高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的中点。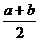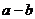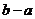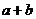则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。等于（  ）

    试题详情

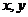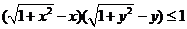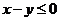
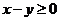
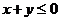
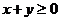
    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。            高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                   高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    12．若实数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。满足高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则　　　　　　　　　（    ）

    试题详情

          高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。      高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。  高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。　　　 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。  高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。           高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

     

     

     

    第Ⅱ卷（非选择题　共90分）

    试题详情

    二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.

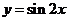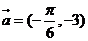    13．将函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。按向量高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。平移后得到的函数表达式是           ；

    试题详情

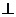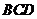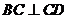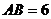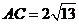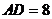    14．已知点A，B，C，D在同一球面上，AB高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。平面高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，若高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则B、C两点间的球面距离是        ；

    试题详情

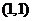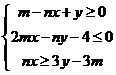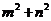    15．如果点高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。在不等式组高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。所表示的平面区域内，则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的取值范围是    ；

    试题详情

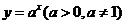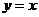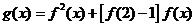    16．已知函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。与高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的图象关于直线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。对称，

    试题详情

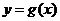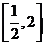    设高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，若高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。在区间高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。上是增函数，则实数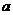高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的取值范围是        ．

    试题详情

    三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.

    17．（本题满分12分）

    试题详情

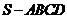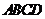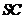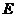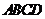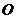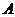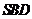    已知四棱锥高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的底面高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。是正方形，侧棱高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的中点高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。在底面内的射影恰好是正方形高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的中心高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，顶点高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。在截面高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。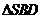内的射影恰好是高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。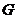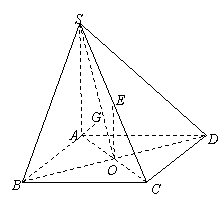的重心高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。．

    试题详情

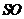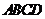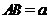    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。（1）求直线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。与底面高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。所成角的正切值；

    试题详情

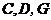    （2）设高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，求此四棱锥过点高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的截面面积．

     

     

     

     

     

     

     

     

     

     

     

    试题详情

    18．（本题满分12分）

           某工厂由于工作失误，未贴标签前，把3箱含“三聚氰胺”的问题牛奶与合格的3箱牛

           奶混到了一起。对这6箱牛奶逐箱进行检测，到确定出3箱问题奶粉为止。

       （1）求通过3次检测，就可以把3箱含“三聚氰胺”的牛奶全部筛选出来的概率；

       （2）求最多通过4次检测，就可以把3箱含“三聚氰胺”的牛奶全部筛选很出来的概率。

     

     

     

     

     

     

     

    试题详情

    19．（本题满分12分）

    试题详情

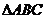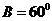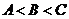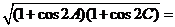
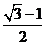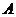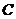    在锐角高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。中，已知高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，且高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。.

    试题详情

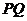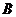    （1）求角高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。与高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的大小；

    试题详情

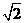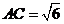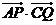    （2）高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。是以高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。为圆心，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。为半径的圆的直径，已知高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，求高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的最大值.

    　

    　

     

     

     

    试题详情

    20．（本题满分12分）

    试题详情

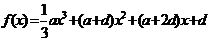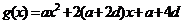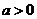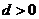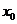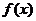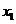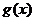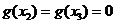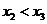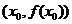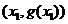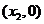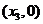    已知函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，其中高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，设高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的极小值点，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的极值点，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。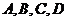，并且高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。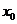，将点高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。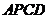，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。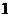，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。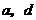，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。依次记为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。．

    试题详情

    （1）求高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的值；

    试题详情

    （2）若四边形高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。为梯形且面积为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，求高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的值．

     

     

     

     

     

     

     

     

     

     

    试题详情

    21．（本题满分12分）

    试题详情

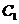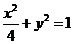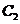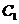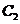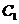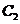    已知椭圆高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的方程为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，双曲线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的左、右焦点分别为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的左、右顶点，而高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的左、右顶点分别是高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的左、右焦点．

    试题详情

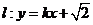        （1）求双曲线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的方程；

    试题详情

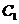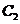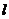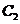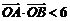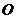        （2）若直线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。与椭圆高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。及双曲线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。都恒有两个不同的交点，且高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。与高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的两个交点A和B满足高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。(其中高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。为原点)，求k的取值范围．

     

     

     

    试题详情

    22．（本题满分14分）

    试题详情

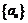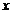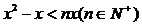    数列高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的通项是关于高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的不等式高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的解集中整数的个数，

    试题详情

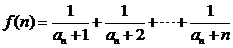    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。．

    试题详情

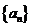    （1）求数列高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的通项公式；

    试题详情

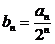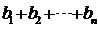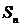    (2) 若高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，求高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的和高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。；

    试题详情

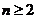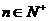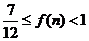    (3) 求证：对高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。且高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 恒有高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。．

     

     

     

     

     

     

     

     

    抚州一中2009届高三第四次模拟考试

    试题详情

    一、选择题

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    B

    A

    B

    D

    D

    C

    A

    A

    B

    A

    C

    D

    二、填空题13.高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；  14.高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；  15.高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；     16.高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

    三、解答题

    １7．（1）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。两两相互垂直, 连结高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。并延长交高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。于F．

        高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

      高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        同理可得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

       高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

       高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。       ------------  (6分)

    （2）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的重心,    F是SB的中点

       高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

       高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

       梯形的高高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。  

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。     ---     (12分)

    【注】可以用空间向量的方法

    18．解：

       （1）设通过3次检测，就可以把3箱含“三聚氰胺”的牛奶全部筛选出来的事件为A

                                                               高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。1分

           P（A）=高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                                    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。5分

           所以通过3次检测，就可以把3箱含“三聚氰胺”的牛奶全部筛选出来的概率为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…6分

    （2）设最多通过4次检测，就可以把3箱含“三聚氰胺”的牛奶全部筛选出来的事件为B … 7分

           P（B）=高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                           高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。11分

           所以最多通过4次检测，就可以把3箱含“三聚氰胺”的牛奶全部筛选出来的概率为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。… 12分

    19．（1）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

    又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.………6分

    （2）

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.从而

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。且同向时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.………12分

    20.解：(1) 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,

    令高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。或高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。处取极小值，即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                                                           …………4分

    （2）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。处取得极小值，即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    由四边形ABCD是梯形及BC与AD不平行，得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    由四边形ABCD的面积为1，得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，从而高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。　　　　　　　　　　　　　　　　　　　　　　　　　　　　……12分

    21．（1）设双曲线C2的方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。= 1，则a2 = 4 ? 1 = 3，再由a2 + b2 = c2得b2 = 1．故C2的方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。= 1．                                                    （5分）

        （2）将y = kx +高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。代入高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得(1 + 4k2)x2 + 8高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。kx + 4 = 0，由直线l与椭圆C1恒有两个不同的交点得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。(8高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。)2k2 ? 16 (1 + 4k2) = 16(4k2 ? 1)＞0，即k2＞高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．①(7分)

    将y = kx + 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。代入高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得(1 ? 3k2)x2 ? 6高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。kx ? 9 = 0．由直线l与双曲线C2恒有两个不同的交点A、B得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．即k≠高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。且k2＜1．②（9分）

    设A (xA，yA)，B (xB，yB)，则xA + xB = 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，xA，xB = 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得xA xB + yA yB＜6，而xA xB + yA yB = xA xB + (kxA + 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。)  (kxb + 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。)= (k2 + 1) xA xB + 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。k (xA + xB) + 2 = (k2 + 1)?高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，于是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。＜6，即将高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．解此不等式得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。或高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．                                  　　　③      （11分）

    由①、②、③得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    故k的取值范围为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．                   （12分）

    22．（1）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    （２）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    （３）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。　　　　　　①

    又由于高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    两式相减得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。且高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时是增函数，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的最小值是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，　　　　②

    由①②得： 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。成立．

     


    同步练习册答案