
江苏省扬州中学2005―2006学年度第一学期期中考试
高二数学试卷
txjy
一 、选择题(每题5分)
1.下列各对双曲线中,既有相同的离心率,又有相同渐近线的是txjy
A. 与
与 B.
B. 与
与
C. 与
与 D.
D. 与
与
2.已知 为椭圆
为椭圆 上三点,若
上三点,若 与三点
与三点 、
、 、
、 的距离为等差数列,则
的距离为等差数列,则 的值为txjy
的值为txjy
A. B.
B. C.
C. D.
D.
3.某曲线 的一条准线方程是
的一条准线方程是 ,则
,则 的值为txjy
的值为txjy
A. B.
B. C.
C. D.
D.
4.已知方程 表示两条直线,则这两条直线的夹角是txjy
表示两条直线,则这两条直线的夹角是txjy
A.0° B.45° C.90° D.135°
5.直线 与圆
与圆 交于P、Q两点,O为坐标原点,则△POQ的面积等于txjy
交于P、Q两点,O为坐标原点,则△POQ的面积等于txjy
A. B.
B. C.
C. D.
D.
6.直线 与两直线
与两直线 和
和 分别相交于P、Q两点,若PQ的中点为R(1,-1),则直线
分别相交于P、Q两点,若PQ的中点为R(1,-1),则直线 的斜率属于下列哪个区间txjy
的斜率属于下列哪个区间txjy
A.(-∞,-1] B.[0,1]
C.[-1,0] D.[1,+∞
7.与点P(1,-1)相距为5,且到y轴的距离等于4的点的个数是
A.2
B.
8.四条直线 围成的图形是txjy
围成的图形是txjy
A.长方形 B.正方形 C.菱形 D.梯形
9.一动圆与圆 外切,同时与圆
外切,同时与圆 内切,则动圆圆心的轨迹为
内切,则动圆圆心的轨迹为
A.直线 B.圆 C.椭圆 D.双曲线的一支
10.已知椭圆 的一条弦所在直线方程是
的一条弦所在直线方程是 ,弦的中点坐标是
,弦的中点坐标是 ,则椭圆的离心率是txjy
,则椭圆的离心率是txjy
A. B.
B. C.
C. D.
D.
11.边长为5的菱形,它的一条对角线长不大于6,另一条不小于6,则这个菱形两条对角线长之和的最大值是
A. B.
B. D.12
D.12
12.长轴为 的椭圆
的椭圆 上有动点
上有动点 (与
(与 不重合,
不重合, 为左,
为左, 为右),直线
为右),直线 交右准线
交右准线 于
于 ,
, ,
, 是椭圆右焦点,则
是椭圆右焦点,则 等于
等于
A.45° B.60° C.90° D.120°
二、填空题(每题4分)
13.A、B两质点的质量分别为
14.等轴双曲线xy = k(k为非零常数)的渐近线方程为______________.
15.已知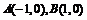 ,点
,点 满足
满足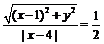 ,则
,则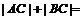 _________.
_________.
16.在椭圆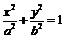 中
中 ,
,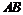 为过左焦点
为过左焦点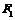 的弦,且
的弦,且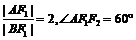 ,则椭圆的离心率
,则椭圆的离心率 ____________.
____________.
17.双曲线 左右顶点为
左右顶点为 ,
,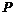 为右支上一点,且
为右支上一点,且 ,则
,则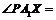 __________度.
__________度.
18.关于曲线C: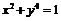 的下列说法:⑴关于点(0,0)对称,⑵关于直线
的下列说法:⑴关于点(0,0)对称,⑵关于直线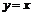 对称,⑶是封闭图形,面积小于
对称,⑶是封闭图形,面积小于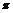 ,⑷是封闭图形,面积大于
,⑷是封闭图形,面积大于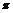 ,⑸不是封闭图形,无面积可言,其中正确的序号是_________________.
,⑸不是封闭图形,无面积可言,其中正确的序号是_________________.
三、解答题(19―22每题13分,23题14分)
19.直线 是
是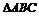 中
中 的平分线所在的直线,若
的平分线所在的直线,若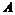 、
、 坐标分别为
坐标分别为 ,
,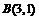 ,判断
,判断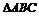 形状,并求面积.
形状,并求面积.
20.双曲线与椭圆在 轴上有公共焦点,若椭圆焦距为
轴上有公共焦点,若椭圆焦距为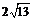 ,它们的离心率是方程
,它们的离心率是方程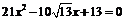 的两根,求双曲线和椭圆的标准方程.
的两根,求双曲线和椭圆的标准方程.
21.已知椭圆的中心在坐标原点,焦点在 轴上,它的一个焦点为
轴上,它的一个焦点为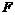 ,
,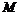 是椭圆上的任意点,
是椭圆上的任意点,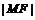 的最大值和最小值的积为4,椭圆上存在以
的最大值和最小值的积为4,椭圆上存在以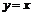 为轴的对称点
为轴的对称点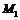 和
和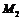 ,且
,且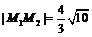 ,求椭圆的方程.
,求椭圆的方程.







 22.已知定点
22.已知定点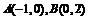 ,过点
,过点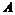 的直线
的直线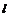 交半圆
交半圆 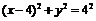
 ≥0
≥0 于P、Q两点,线段PQ中点为M,直线
于P、Q两点,线段PQ中点为M,直线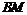 交
交 轴于
轴于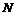 .
.
⑴若点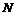 位于点
位于点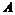 右侧,试求直线
右侧,试求直线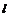 的斜率
的斜率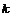 的取值范围.
的取值范围.
⑵若半圆的圆心为D,在⑴的条件下,△PDQ能否为正三角形?
23.椭圆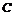 的中心在原点0,它的短轴长为
的中心在原点0,它的短轴长为 ,右焦点为
,右焦点为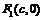 ,右准线
,右准线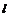 与
与 轴相交于点A,并且
轴相交于点A,并且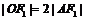 .
.
⑴求椭圆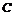 的方程.
的方程.
⑵过椭圆的左焦点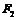 作一条与两坐标轴都不垂直的直线
作一条与两坐标轴都不垂直的直线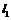 ,交椭圆于
,交椭圆于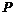 ,
,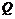 两点,若
两点,若 轴上的某一点
轴上的某一点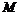 能使得
能使得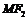 为
为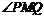 的平分线,则称点
的平分线,则称点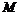 是椭圆的“左特征点”,求出此椭圆的“左特征点”
是椭圆的“左特征点”,求出此椭圆的“左特征点”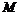 的坐标.
的坐标.
⑶请根据上面的结论猜想:椭圆 的“左特征点”
的“左特征点”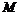 是怎样的点?并证明你的结论。
是怎样的点?并证明你的结论。
四、附加题(10分,计入总分,但总分不得超过150分)
24.下面的图形既可看作是圆的一部分,也可以看作是椭圆的一部分,也可以看作是双曲线某一支的一部分,且只能是上述中的某一种你现有直尺、圆规和笔,你如何判断它们是上述曲线中的哪一类,写出判断的方法和依据.

一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
C
C
A
C
B
C
C
B
B
C
二、填空题
13.( ) 14.x=0或y=0 15.4 16.2/3 17.20 18.①④
) 14.x=0或y=0 15.4 16.2/3 17.20 18.①④
三、解答题
19.解:A(―4,2)关于直线 :
: 对称的点为
对称的点为 ,因为直线
,因为直线 是
是 中
中 的平分线,可以点
的平分线,可以点 在直线
在直线 上,故直线
上,故直线 的方程是
的方程是 ,由
,由 ,
, ,则
,则 是以
是以 为直角的三角形,
为直角的三角形, ,
, 10
10
20.解:由 ,
, ,设双曲线方程为
,设双曲线方程为 ,椭圆方程为
,椭圆方程为 ,它们的焦点
,它们的焦点 ,则
,则

 ,又
,又 ,
, ,
, 双曲线方程为
双曲线方程为 ,椭圆方程为
,椭圆方程为
21.解: ,设椭圆方程为
,设椭圆方程为 ①,设过
①,设过 和
和 的直线方程为
的直线方程为 ②,将②代入①得
②,将②代入①得 -
- ③,设
③,设 ,
, 的中点为
的中点为
 代入
代入 ,
, ,
, ,由③
,由③
 ,
, ,解得
,解得
22.解:⑴设直线 方程为:
方程为: 代入
代入 ,得
,得
 ,另知直线
,另知直线 与半圆相交的条件为
与半圆相交的条件为 ,设
,设 ,则
,则 ,
, ,点
,点 位于
位于 的右侧,应有
的右侧,应有 ,即
,即 ,
, (亦可求出
(亦可求出 的横坐标
的横坐标 )
)
⑵若 为正
为正 ,则点
,则点 到直线
到直线 距离
距离


 与
与 矛盾,
矛盾, 在⑴条件下不可能是正△.
在⑴条件下不可能是正△.
 23.⑴由题意设椭圆方程为:
23.⑴由题意设椭圆方程为: ,则
,则 解得:
解得:  ,所以椭圆方程为:
,所以椭圆方程为:
⑵设“左特征点” ,设
,设 ,
, 为
为 的平分线,
的平分线, ,
, ,下面设直线
,下面设直线 的方程为
的方程为 ,代入
,代入 得:
得: ,
, 代入上式得
代入上式得 解得
解得
⑶椭圆 的“左特征点”M是椭圆的左准线和x轴的交点证明如下:
的“左特征点”M是椭圆的左准线和x轴的交点证明如下:
证明:设椭圆的左准线 与x轴相交于点M,过点A、B分别作
与x轴相交于点M,过点A、B分别作 的垂线,垂足分别为点C、D。据椭圆第二定义得
的垂线,垂足分别为点C、D。据椭圆第二定义得 ,
,
∵ ∥
∥ ∥
∥ ,∴
,∴ ,
,
∴ ∵
∵ 与
与 均为锐角,∴
均为锐角,∴ 。
。
∴ 。∴
。∴ 为
为 的平分线。故点
的平分线。故点 为椭圆的“左特征点”。
为椭圆的“左特征点”。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com