
2007届福鼎一中高三月考(10.5)
数学(理)试卷
第一卷 (选择题,共60分)
一、选择题(每题有且只有一个答案正确)(60分)
1. 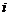 是虚数单位,
是虚数单位,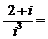 ( )
( )
A. 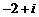 B.
B.
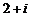 C.
C.
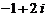 D.
D. 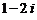
2.函数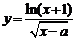 的定义域是
的定义域是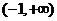 ,则实数
,则实数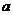 取值集合是( )
取值集合是( )
A.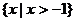 B.
B.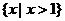 C.
C.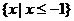 D.
D.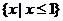
3.已知集合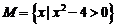 ,
,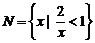 ,则M∩N等于( )
,则M∩N等于( )
A.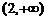 B.
B. C.N
D.M
C.N
D.M
4.设 , 则
, 则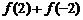 的值为( )
的值为( )
A 2 B 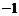 C 0 D 2
C 0 D 2
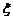
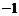
0
1
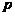
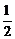
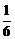
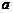
5. 设随机变量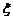 的分布列为右表,
的分布列为右表,
则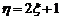 的期望
的期望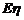 的值为( )
的值为( )
A 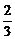 B
B 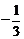 C
C 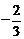 D
D 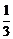
6.对于集合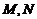 ,定义
,定义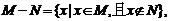
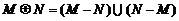 ,
,
设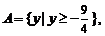
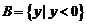 , 则
, 则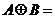 ( )
( )
A.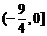 B.
B. C.
C. D.
D.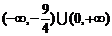
7.已知直线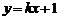 与曲线
与曲线 切于点
切于点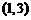 ,则
,则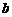 的值为( )
的值为( )
A 3 B 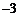 C
C 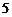 D
D 
8. 若方程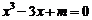 在
在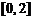 上有解,则实数
上有解,则实数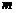 的取值范围是 ( )
的取值范围是 ( )
A.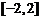 B.
B.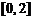 C.
C.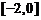 D.
D. ∪
∪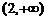
9. 设函数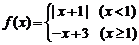 ,则使得
,则使得 的自变量
的自变量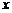 的取值范围是 ( )
的取值范围是 ( )
A.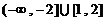 B.
B.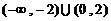 C.
C.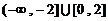 D.
D.

10.给出下列命题:①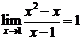 ,②
,②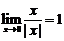 ,③
,③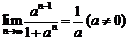 ,④已知
,④已知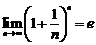 ,则
,则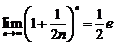 ;其中正确命题的个数为( )
;其中正确命题的个数为( )
A 1
B
11.命题 ,若
,若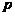 是
是 的充分非必要条件,则实数
的充分非必要条件,则实数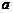 的取值范围是( ) A
的取值范围是( ) A 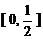 B
B 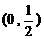 C
C 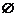 D
D 
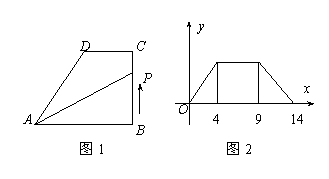 12.直角梯形ABCD如图1所示,动点
12.直角梯形ABCD如图1所示,动点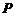 从
从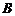 点出发,由
点出发,由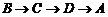 沿边运动。设点
沿边运动。设点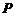 运动的路程为
运动的路程为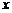 ,
,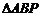 的面积为
的面积为 ,如果
,如果 的图象如图2所示,则
的图象如图2所示,则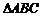 的面积为 ( ) A 10 B
的面积为 ( ) A 10 B
第二卷 (非选择题共90分)
二、填空题(16分)
13. 若复数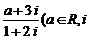 为虚数单位.)是纯虚数,则实数a的值为 __________
为虚数单位.)是纯虚数,则实数a的值为 __________
14.已知函数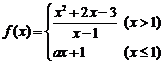 在
在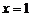 处连续,则实数
处连续,则实数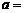 ________
________
15.  从全校参加科技知识竞赛的学生试卷中,抽取一个样本,考察竞赛的成绩分布。现将样本分成5组,绘成频率分布直方图(如下图),图中从左到右各小组的小长方形的高的比是1∶3∶6∶4∶2,最右边一组的频数是6.
从全校参加科技知识竞赛的学生试卷中,抽取一个样本,考察竞赛的成绩分布。现将样本分成5组,绘成频率分布直方图(如下图),图中从左到右各小组的小长方形的高的比是1∶3∶6∶4∶2,最右边一组的频数是6.
请结合直方图提供的信息,回答该样本的容量
是_________。
16.在正项数列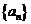 中,
中, 表示其前
表示其前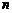 项和,且
项和,且 ,则
,则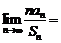 ________
________
 2007年福鼎一中高三月考(10.5)
2007年福鼎一中高三月考(10.5)
数 学(理)试卷
一.选择题:(每题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
 答案
答案
二. 填空题:(每题4分,共16分)
⒔___________ ⒕____________ ⒖______________ ⒗_______________
三. 解答题:(17―21题每题12 分,22题14分,共74分)
17. (12分)设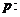 函数
函数 的定义域为
的定义域为 ;
;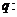 函数
函数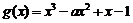 在
在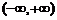 上有极大值也有极小值。若
上有极大值也有极小值。若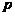 和
和 有且只有一个为真,求实数
有且只有一个为真,求实数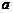 的取值范围。
的取值范围。
18. (12分)某商店进货每件50元,据市场调查,销售价格(每件x元)在50≤x≤80时,每天售出的件数与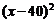 成反比(比例系数为正常数
成反比(比例系数为正常数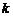 )。若想每天获得的利润最多,该商店的销售价格每件应定为多少元?
)。若想每天获得的利润最多,该商店的销售价格每件应定为多少元?

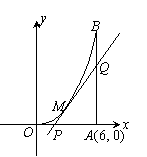
19. (12分)如图所示,曲线段OMB是函数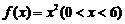 的图像,
的图像,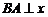 轴于A,曲线段OMB上一点
轴于A,曲线段OMB上一点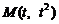
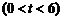 处的切线PQ交x轴于P,交线段AB于Q.
处的切线PQ交x轴于P,交线段AB于Q.
(1)试用t表示切线PQ的方程;
 (2)设△QAP的面积为
(2)设△QAP的面积为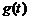 ,求函数
,求函数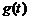 最大值。
最大值。
20. (12分)某人用骰子(各面上分别标以1到6的均匀正方体玩具)做抛掷得分游戏,规则如下:若抛出的点数为3的倍数,则得1分,否则得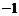 分.
分.
(1)求抛掷4次恰得2分的概率;(2)求抛掷4次所得分数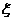 的分布列和数学期望.
的分布列和数学期望.
21.(12分)已知函数
(1)求函数 的单调区间;
的单调区间;
(2)若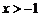 ,证明:
,证明: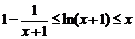
 22.(14分)设
22.(14分)设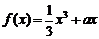 ,且
,且 在
在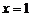 处有极小值。
处有极小值。
(1)若 在区间
在区间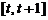 上为减函数,求实数
上为减函数,求实数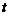 的取值范围。
的取值范围。
(2)数列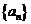 满足
满足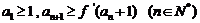
① 用数学归纳法证明: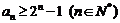
②
比较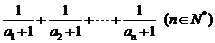 与1的大小。
与1的大小。
 |
答案:CCDCA CAACA AB
13.  14.
14.  15.
15. 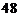 16. 2
16. 2
17. 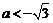 或
或
18. 设定价为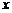 元,则每天获得的利润为
元,则每天获得的利润为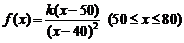
当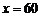 时,
时, 最大。
最大。
19.(1)切线: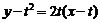 (2)
(2)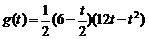 ,当
,当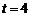 时
时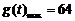
20. (1)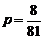
(2)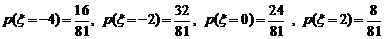 ,
,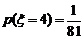
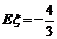
21.(1)递增区间为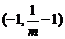 ,递减区间为
,递减区间为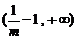
22.(1)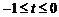 (3)
(3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com