
四川省绵阳中学2009届高三二诊模拟试题
文科数学
总分:150分 时间:120分钟
一、 选择题(12 5分=60分)
5分=60分)
1、设 ,
, ,则
,则 是
【 】
是
【 】
A. B.
B. C.
C. D.
D.
2、将函数 的图像按向量
的图像按向量 平移后得到
平移后得到 的图像,则
的图像,则 【 】
【 】
A. B.
B. C.
C. D.
D.
3、已实数 、
、 满足条件
满足条件 ,如果目标函数
,如果目标函数 的最小值是
的最小值是 ,则实数
,则实数 等于
【 】
等于
【 】
A.7 B.
4、函数 与
与 的图像关于
的图像关于 对称,而函数
对称,而函数 的图像与
的图像与 的图像关于
的图像关于 轴对称且
轴对称且 ,则
,则 【 】
【 】
A. B.
B. C.
C. D.
D.
5、在数列 中,
中, 
 ,则
,则 【 】
【 】
A. B.
B. C.
C. D.
D.
6、在 中,角
中,角 所对边的长分别为
所对边的长分别为 且
且
则 【 】
【 】
A. B.
B. C.
C. 或
或 D.
D. 或
或
7、设函数 ,则
,则 是
【 】
是
【 】
A.最小正周期为 的奇函数 B.最小正周期为
的奇函数 B.最小正周期为 的偶函数
的偶函数
C.最小正周期为 的奇函数 D.最小正周期为
的奇函数 D.最小正周期为 的偶函数
的偶函数
8、等腰三角形两腰所在的直线方程分别是 和
和 ,原点在此等腰三角形的底边上,则底边所在直线的斜率为
【 】
,原点在此等腰三角形的底边上,则底边所在直线的斜率为
【 】
A. B.
B. C.
C. D.
D.
9、一个容量为20的样本数据,分组后,组别与频数如下:
组别






频数
2
3
4
5
4
2
则样本在 上的频率为
【 】
上的频率为
【 】
A. ㄇ B.
ㄇ B. ㄇ C.
ㄇ C. ㄇ D.
ㄇ D. ㄇ
ㄇ
10、圆 被直线
被直线 所截得的弦长为
所截得的弦长为 ,则实数
,则实数 的值是 【 】
的值是 【 】
A. B.
B. C.
C. D.
D.
11、若 ,则
,则 【 】
【 】
A. B.
B. C.
C. D.
D.
12、设函数 是定义在
是定义在 上的奇函数,若
上的奇函数,若 的最小正周期为3,且
的最小正周期为3,且 ,
, ,则
,则 的取值范围是
【 】
的取值范围是
【 】
A. B.
B. tesoon
tesoon
C. 或
或 D.
D. 或
或
二、 填空题(4 4分=16分)
4分=16分)
13、已知向量 与
与 的夹角为
的夹角为 且
且 ,则
,则
 的值为
的值为
14、过 作圆
作圆 的切线,切点为
的切线,切点为 ,则过
,则过 两点的直线方程是
两点的直线方程是
15、设 则函数
则函数 的最小值是
的最小值是
16、关于函数 ,有下列命题:①周期是
,有下列命题:①周期是 ;②关于直线
;②关于直线 对称,③图象关于点
对称,③图象关于点 对称;④在区间
对称;④在区间 上单调递增,其正确命题的序号是______________________________
上单调递增,其正确命题的序号是______________________________
三、解答题(共74分)
17、(12分)函数 ,其中
,其中 ,
,
 其中
其中 ,若相邻两对称轴间的距离不小于
,若相邻两对称轴间的距离不小于 .
.
(1)求 的取值范围.
的取值范围.
(2)在 中,
中,  分别是角
分别是角 的对边,
的对边,  ,当
,当 最大时,
最大时,  ,求
,求 的面积
的面积
18、(12分)甲、乙两队参加奥运知识竞赛,每对3人,每人回答一个问题,答对者为本队赢得1分,答错时得0分。假设甲队中每人答对的概率均为 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ,
, ,
, 。且各人回答正确与否相互之间无影响,用
。且各人回答正确与否相互之间无影响,用 表示甲队总得分为
表示甲队总得分为 分(
分( )
)
(1)求 和
和
(2)用 表示“甲乙两队总得分之和等于3分”这一事件,用
表示“甲乙两队总得分之和等于3分”这一事件,用 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求
19、(13分)已知⊙ ,直线
,直线
(1)求证:当 时,直线
时,直线 与⊙
与⊙ 恒有两个不同的交点;
恒有两个不同的交点;
(2)设直线 与⊙
与⊙ 交于
交于 两点,若
两点,若 ,求直线
,求直线 的倾斜角;
的倾斜角;
(3)求弦 的中点
的中点 的轨迹方程
的轨迹方程
20、(12) 在数列 和
和 中,
中, ,数列
,数列 的前
的前 项和为
项和为 ,且www.tesoon.com
,且www.tesoon.com ,
, 为
为 与
与 的等比中项。
的等比中项。
(1) 求 的值;(2)求数列
的值;(2)求数列 和
和 的通项公式;
的通项公式;
(2) 设 ,求数列
,求数列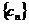 的前
的前 项和
项和
21、(12分) 已知函数 ,其中
,其中 ,
, 为参数,且
为参数,且

(1)当 时,判断函数
时,判断函数 是否有极值;
是否有极值;
(2)要使函数 的极小值大于0,求参数
的极小值大于0,求参数 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数 ,函数
,函数 在区间
在区间 内都是增函数,求实数
内都是增函数,求实数 的取值范围
的取值范围
四川省绵阳中学2009届高三二诊模拟试题
文科数学答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
B
B
A
D
D
A
C
D
B
D
二、填空题(4 4分=16分)
4分=16分)
13、 0 ; 14、 ; 15、
; 15、 ; 16、
③ ;
; 16、
③ ;
三、解答题(共74分)
17、(15分) (1) (2)
(2)  的面积是:
的面积是:
18、(14分) (1)
 (2)
(2)
19、(15分)
(1)略
(2)直线 的倾斜角为:
的倾斜角为: 或
或
(3)弦 的中点
的中点 的轨迹方程是:
的轨迹方程是:
20、(15分)
(1) ; (2)
; (2) ;
;
(3)数列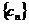 的前
的前 项和
项和
21、(15分)
(1)当 时,
时,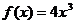 在
在 上单调递增,所以
上单调递增,所以 无极值;
无极值;
(2)参数 的取值范围是:
的取值范围是: 或
或 ;
;
(3)实数 的取值范围是:
的取值范围是: 或
或
 天星教育网(www.tesoon.com)
版权所有
天星教育网(www.tesoon.com)
版权所有
天星教育网(www.tesoon.com) 版权所有
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com