
高2009级一诊模拟(文科)数学试题
一.选择题:(每小题5分,共60分)
1.设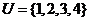 ,且
,且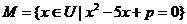 ,若
,若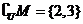 ,则实数
,则实数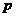 的值为
的值为
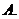
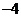

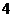
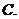
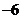
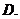
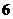
2.等差数列{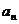 }中,若
}中,若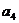 +
+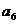 +
+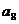 +
+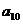 +
+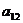 =120,则
=120,则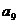 -
-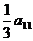 的值是
的值是
A.14 B.
3.已知向量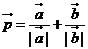 ,其中
,其中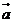 、
、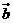 均为非零向量,则
均为非零向量,则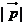 的取值范围是
的取值范围是
A.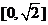 B。
B。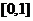 C。
C。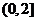 D。
D。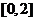
4.编号为1、2、3、4、5的五个人分别去坐编号为1、2、3、4、5的五个座位,其中有且只有两个的编号与座位号一致的坐法是
A 10种 B 20种 C 30种 D 60种
5.若(1+mx)6=a0+a1x+a2x2+…+a6x6且a1+a2+…+a6=63,则实数m的值为.
A.
1
B.
6.一射手对同一目标独立地射击四次,已知至少命中一次的概率为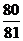 ,则此射手每次射击命中的概率为
,则此射手每次射击命中的概率为
A. B. C. D.
7. 当x>1时,不等式x+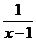 ≥a恒成立,则实数a的取值范围是
≥a恒成立,则实数a的取值范围是
 A.(-∞,2] B.[2,+∞) C.[3,+∞) D.(-∞,3]
A.(-∞,2] B.[2,+∞) C.[3,+∞) D.(-∞,3]
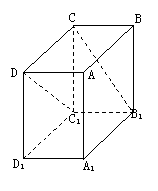
8.在长方体ABCD-A1B
A.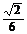 B.
B. 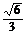 C.
C. 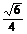 D.
D. 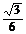
9.函数y=2x3-3x2-12x+5在区间[0,3]上最大值与最小值分别是
A. 5,-15 B. 5,
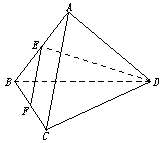 10.如图在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的外接球的体积是
10.如图在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的外接球的体积是

11.已知函数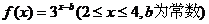 的图象经过点
的图象经过点
(2,1),则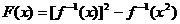 的值域为
的值域为
A.[2,5] B.[1,+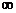 ] C.[2,10] D.[2,13]
] C.[2,10] D.[2,13]
 12.定义在R上的函数
12.定义在R上的函数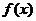 满足
满足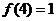 .
.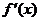 为
为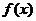 的导函数,已知函数
的导函数,已知函数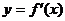 的图象如右图所示.若两正数
的图象如右图所示.若两正数 满足
满足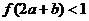 ,则
,则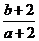 的取值范围是
的取值范围是
A.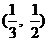 B.
B.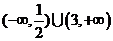 C.
C.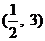 D.
D.
二.填空题:(每小题4分,共16分)
 13.已知函数
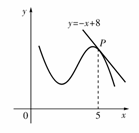
13.已知函数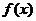 是奇函数,当
是奇函数,当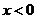 时,
时,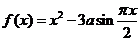 ,且
,且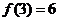 ,则实数
,则实数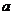 =___ .
=___ .
14.如图,函数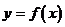 的图象在点P处的切线方程是
的图象在点P处的切线方程是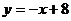 ,则
,则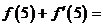 _____
_____
15.设函数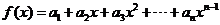 ,
,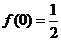 ,数列
,数列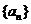 满足
满足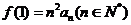 ,则数列
,则数列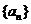 的通项
的通项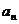 等于
.
等于
.
16.下列命题:
① 函数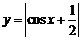 的最小正周期是
的最小正周期是 ;
;
②函数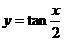 的图像的对称中心是
的图像的对称中心是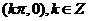 ;
;
③ 函数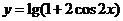 的递减区间是[
的递减区间是[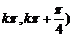
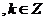 ;
;
④ 函数 的图像可由函数
的图像可由函数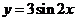 的图像按向量
的图像按向量 平移得到。
平移得到。
其中正确的命题序号是 。
13
14
15
16
三.解答题:
17. (12分)已知△ABC的面积S满足3≤S≤3 且
且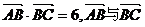 的夹角为
的夹角为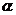 ,
,
(Ⅰ)求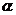 的取值范围;
的取值范围;
(Ⅱ)求 的最小值。
的最小值。
18. (12分)某工厂为了保障安全生产,每月初组织工人参加一次技能测试. 甲、乙两名工人通过每次测试的概率分别是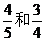 . 假设两人参加测试是否通过相互之间没有影响.
. 假设两人参加测试是否通过相互之间没有影响.
(I)求甲工人连续3个月参加技能测试至少1次未通过的概率;
(II)求甲、乙两人各连续3个月参加技能测试,甲工人恰好通过2次且乙工人恰好通过1次的概率;
(III)工厂规定:工人连续2次没通过测试,则被撤销上岗资格. 求乙工人恰好参加4次测试后被撤销上岗资格的概率.
 19. (12分)已知斜三棱柱
19. (12分)已知斜三棱柱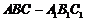 ,
,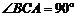 ,
,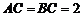 ,
,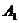 在底面
在底面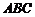 上的射影恰为
上的射影恰为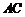 的中点
的中点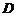 ,又知
,又知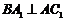 .
.
(Ⅰ)求证: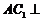 平面
平面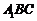 ;
;
(Ⅱ)求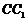 到平面
到平面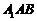 的距离;
的距离;
(Ⅲ)求二面角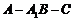 的大小.
的大小.
(I)求证:数列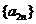 与
与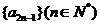 都是等比数列;
都是等比数列;
(II)求数列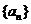 前
前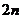 的和
的和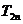 ;
;
(III)若数列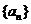 前
前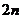 的和为
的和为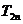 ,不等式
,不等式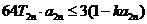 对
对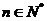 恒成立,求
恒成立,求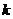 的最大值.
的最大值.
21. (12分)已知二次函数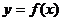 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为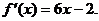 数列{
数列{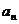 }的前n项和为
}的前n项和为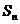 ,点
,点 均在函数
均在函数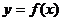 的图像上.
的图像上.
(I)求数列{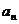 }的通项公式;
}的通项公式;
(II)设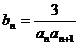 ,
,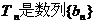 的前n项和,求使得
的前n项和,求使得 对所有
对所有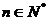 都成立的最小正整数m.
都成立的最小正整数m.
22. (14分)已知定义在R上的函数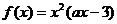 ,其中
,其中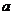 为常数.
为常数.
(I)若x =1是函数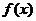 的一个极值点,求
的一个极值点,求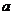 的值;
的值;
(II)若函数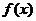 在区间(-1,0)上是增函数,求
在区间(-1,0)上是增函数,求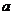 的取值范围;
的取值范围;
(III)若函数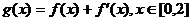 ,在x = 0处取得最大值,求正数
,在x = 0处取得最大值,求正数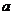 的取值范围.
的取值范围.
成都七中高2009级一诊模拟数学试题(文科) 答案
一.选择题:
1.B.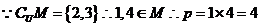
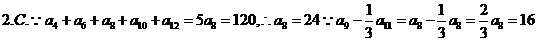
3.D.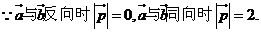
4.B.坐法有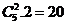
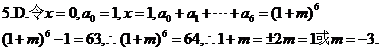
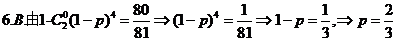
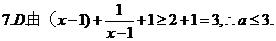
8.C.
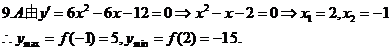
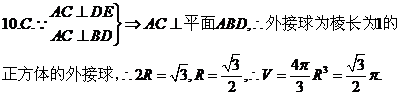
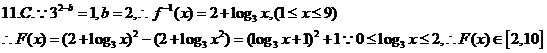
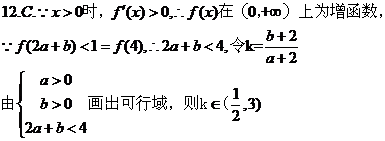
二.填空题:
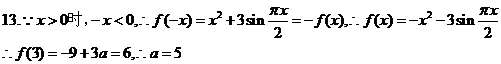
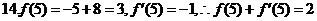
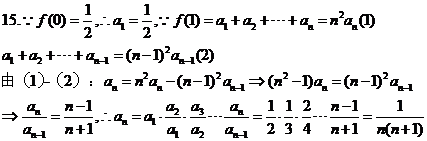
16.①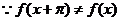 不正确;
不正确;
②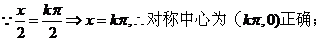
③
④应按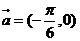 平移,所以不正确.
平移,所以不正确.
三.解答题:
17.解(Ⅰ)由题意知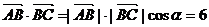
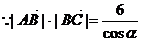
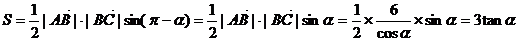
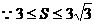 …………3分,
…………3分,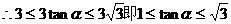 …………4分
…………4分
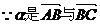 的夹角
的夹角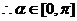
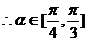 ……………………6分
……………………6分
(Ⅱ)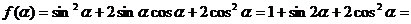
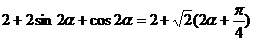 ……………………9分
……………………9分
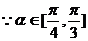
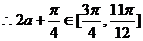
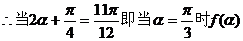 有最小值,
有最小值,
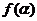 的最小值是
的最小值是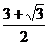 ……………12分
……………12分
18.解:(I)记“甲工人连续3个月参加技能测试,至少有1次未通过”为事件A1,
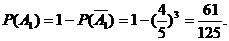 ………………5分
………………5分
(II)记“连续3个月参加技能测试,甲工人恰好通过2次”为事件A2,“连续3个月参加技能测试,乙工人恰好通过1次”为事件B1,则
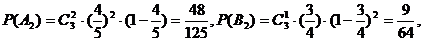
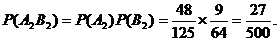
两人各连续3月参加技能测试,甲工人恰好2次通过且乙工人恰好1次通过的概率为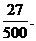 ………………………………………………………………………………10分
………………………………………………………………………………10分
(III)记“乙恰好测试4次后,被撤销上岗资格”为事件A3,
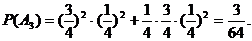 …………12分
…………12分
19.解法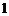 :(Ⅰ)∵
:(Ⅰ)∵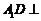 平面
平面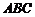 ,∴平面
,∴平面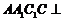 平面
平面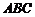 ,
,
又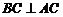 ,∴
,∴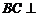 平面
平面 , 得
, 得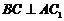 ,又
,又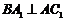 ,
,
 ∴
∴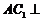 平面
平面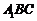 .…………………4分
.…………………4分
(Ⅱ)∵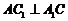 ,四边形
,四边形 为菱形,故
为菱形,故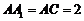 ,
,
又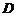 为
为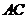 中点,知∴
中点,知∴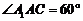 .取
.取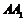 中点
中点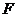 ,则
,则
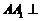 平面
平面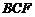 ,从而面
,从而面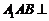 面
面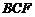 ,…………6分
,…………6分
过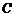 作
作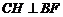 于
于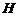 ,则
,则 面
面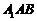 ,在
,在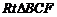 中,
中,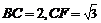 ,故
,故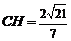 ,即
,即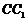 到平面
到平面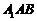 的距离为
的距离为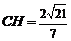 .…………………8分
.…………………8分
(Ⅲ)过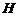 作
作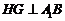 于
于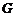 ,连
,连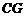 ,则
,则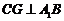 ,从而
,从而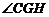 为二面角
为二面角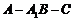 的平面角,在
的平面角,在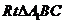 中,
中,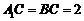 ,∴
,∴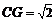 ,…………10分
,…………10分
在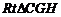 中,
中,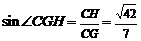 ,故二面角
,故二面角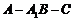 的大小为
的大小为 .
.
…………………12分
 解法
解法 :(Ⅰ)如图,取
:(Ⅰ)如图,取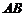 的中点
的中点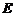 ,则
,则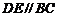 ,∵
,∵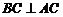 ,∴
,∴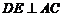 ,
,
又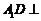 平面
平面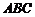 ,以
,以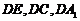 为
为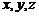 轴建立空间坐标系, …………1分
轴建立空间坐标系, …………1分
则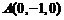 ,
,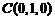 ,
,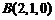 ,
,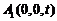 ,
,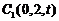 ,
,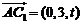 ,
,
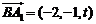 ,
,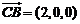 ,由
,由 ,知
,知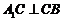 ,
,
又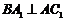 ,从而
,从而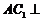 平面
平面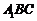 .…………………4分
.…………………4分
(Ⅱ)由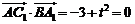 ,得
,得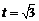 .设平面
.设平面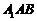 的法向量
的法向量
为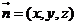 ,
,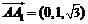 ,
,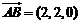 ,
,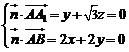 ,
,
设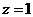 ,则
,则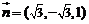 .…………6分
.…………6分
∴点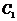 到平面
到平面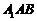 的距离
的距离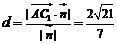 .…………………8分
.…………………8分
(Ⅲ)设面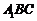 的法向量为
的法向量为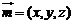 ,
,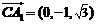 ,
,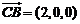 ,
,
∴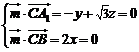 .…………10分
.…………10分
设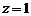 ,则
,则 ,故
,故 ,根据法向量的方向
,根据法向量的方向
可知二面角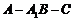 的大小为
的大小为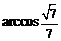 .…………………12分
.…………………12分
20. 解:(1)∵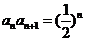 ,∴
,∴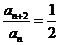 2分
2分
∴数列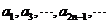 是以1为首项,
是以1为首项,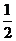 为公比的等比数列;
为公比的等比数列;
(2)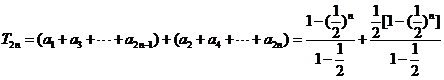
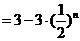 9分
9分
(3)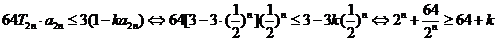
21. 解:(I)设这二次函数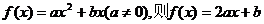 ,
,
由于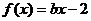 ,得
,得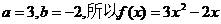 …………2分
…………2分
又因为点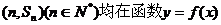 的图像上,所以
的图像上,所以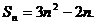
当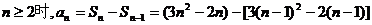
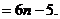 …………6分
…………6分
(II)由(I)得知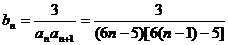
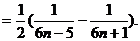 …………7分
…………7分
故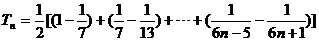
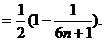 …………9分
…………9分
因此,要使 ,必须且仅须满足
,必须且仅须满足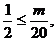
即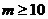 , …………11分
, …………11分
所以满足要求的最小正整数m为10。 …………12分
22. 解:(I)
 的一个极值点,
的一个极值点,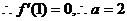 ;………………3分
;………………3分
(II)①当a=0时,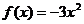 在区间(-1,0)上是增函数,
在区间(-1,0)上是增函数,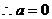 符合题意;
符合题意;
②当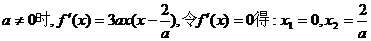 ;
;
当a>0时,对任意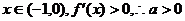 符合题意;
符合题意;
当a<0时,当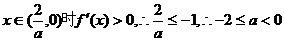 符合题意;
符合题意;
综上所述,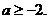 ………………………………………………8分
………………………………………………8分
(III)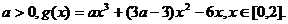
 ………………10分
………………10分
令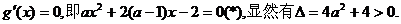
设方程(*)的两个根为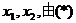 式得
式得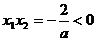 ,不妨设
,不妨设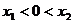 .
.
当 时,
时,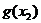 为极小值,所以
为极小值,所以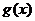 在[0,2]上的最大值只能为
在[0,2]上的最大值只能为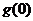 或
或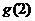 ;
;
当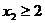 时,由于
时,由于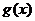 在[0,2]上是单调递减函数,所以最大值为
在[0,2]上是单调递减函数,所以最大值为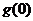 ,所以在[0,2]上的最大值只能为
,所以在[0,2]上的最大值只能为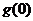 或
或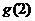 ,
,
又已知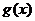 在x=0处取得最大值,所以
在x=0处取得最大值,所以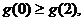 ……………………12分
……………………12分
即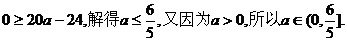 …………14分
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com