湖北省武昌区2009届高三年级元月调研考试
理 科 数 学 2009.1.6
本试卷满分150分，考试用时120分钟.
注意事项:
1.答卷前,考生务必将自已的姓名、准考证号填写在试题卷和答题卡上，并将准考证
号条形码粘贴在答题卡上的指定位置。
2．选择题选出答案后，有2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，
用橡皮擦干净后，再选涂其他答案标号。非选择题用黑色墨水的签字笔直接答在答题卡
上。答在试题卷上无效。
参考公式：
如果事件A、B互斥，那么
如果事件A、B相互独立，那么
如果事件A在一次试验中发生的概率是
，那么n次独立重复试验中恰好发生k次的概率
球的表面积公式
，其中
表示球的半径
球的体积公式
，其中表示球的半径
一.选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1．设集合
，
，则（ ）
A．
B．
C.
D．
2．
（ ）
A．
B．
C．
D．
3．已知复数
满足
（
为虚数单位），则的共轭复数
的虚部是（ ）
A.
B.
C. 
D.
4．若圆
的半径为1，圆心在第一象限，且与直线
和
轴都相切，则该圆的标准方程是（ ）
A．
B．
C．
D．
5.若二项式
的展开式中各项系数的和是512，则展开式中的常数项为（ ）
A.
B.
C.
D. 
6．在等比数列
中,
,前
项和为
.若数列
也成等比数列,则等于（ ）
A.
B.
C. 
D.
7．若随机变量
服从正态分布~
，
，则随机变量
的期望是（ ）
A．
B.
C. 
D. 
8．把函数
的图象按向量
平移后，得到函数
的图象，若函数
的图象与的图象关于直线
对称，则
的解析式是（ ）
A.
B.
C.
D.
9．已知函数f (x)
的图象如图所示，
是函数f (x)的导函数，且
是奇函数，给出以下结论:
①
； ②
；
③
；
④
.
其中一定正确的是 ( )
A. ①③ B. ①④ C. ②③ D. ②④
10．已知函数
，则对于任意实数
、
（
），
的值（ ）
A.恒大于0 B.恒等于
二.填空题：本大题共5小题，每小题5分，共25分.把答案填在答题卡相应位置上.
11. 过点
的直线
与曲线：
相交于
两点,若点
是弦
的中点，则直线的方程为______________________.
12. 给出下列命题: ①垂直高考资源网版权所有于同一直线的两条直线平行;②若一条直线垂直于两条平行线中的一条，则它垂直于另一条;③若一条直线与两条平行线中的一条相交，则它与另一条相交;④一条直线至多与两条异面直线中的一条相交.
其中正确命题的序号是____________ (写出所有正确命题的序号).
13．数列
=
.
14.如果在一周内(周一至周日)安排三所学校的学生参观某展览馆，每天最多只安排一所
学校，要求甲学校连续参观两天，其余两所学校均只参观一天，那么不同的安排方法
共有_____种.
15．已知
是△
的外心，
，
，
.设
，
,若
，则
______________.
三．解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤.
16．（本小题满分12分）
设函数
，其中向量
，
，且
．
（Ⅰ）求实数
的值；
（Ⅱ）求函数
在区间
上的最大值．
17．（本小题满分12分）
某工厂规定，如果工人在一个季度里有1个月完成生产任务，可得奖金90元；如果有2个月完成生产任务，可得奖金210元；如果有3个月完成生产任务，可得奖金330元；如果工人三个月都未完成任务，则没有奖金.假设某工人每月完成任务与否是等可能的，求此工人在一个季度里所得奖金的期望.
18．（本小题满分12分）
已知四棱锥 
的底面是直角梯形，
∥
，
，
，侧面
底面
.
（Ⅰ）求证:
；
（Ⅱ）求二面角
的正切值.
19. （本小题满分12分）
平面直角坐标系中，O为坐标原点，给定两点A（1，0）、B（0，－2），点C满足
、
.
（Ⅰ）求点C的轨迹方程；
（Ⅱ）设点C的轨迹与双曲线
交于两点M、N，且以MN为直径的圆过原点，求证
；
（Ⅲ）在（Ⅱ）的条件下，若双曲线的离心率不大于
，求双曲线实轴长的取值范围.
20．（本小题满分13分）
已知函数
.
(Ⅰ)若
在
上是增函数,求实数
的取值范围；
(Ⅱ)是否存在正实数,使得的导函数
有最大值
?若存在,求出的值;若不存在,请说明理由.
21．（本小题满分14分）
已知数列
（Ⅰ）求数列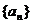
的通项公式；
（Ⅱ）设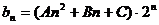
，试推断是否存在常数A，B，C，使对一切
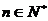都有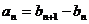
成立？说明你的理由；
（Ⅲ）求证：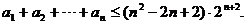
湖北省武昌区2009届高三年级元月调研考试
一.选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
B
C
A
C
B
A
二.填空题
11. 
12. ② 13． 14.
120 15． 
三.解答题
16．解：（Ⅰ）
. …………………………………3分
由
，得
．
………………………………5分
（Ⅱ）由（Ⅰ）得
. ………………8分
由
,得
.
当
,即时,函数
有最大值
. ……………………12分
17．解：设此工人一个季度里所得奖金为，则是一个离散型随机变量.由于该工人每月完成任务与否是等可能的,所以他每月完成任务的概率等于. …………………2分
所以, 
,
,
,
. …………8分
于是
.
所以此工人在一个季度里所得奖金的期望为153. 75元. ……………………12分
18．解：（Ⅰ）取BC的中点H,连结PH, 连结AH交BD于E.
. ……………………………2分
又面
面
,
面.
,
.
,
.
,即
. ………………………………………………4分
因为AH为PA在平面上的射影,
. ……………………………6分
（Ⅱ）连结PE,则由（Ⅰ）知
.
为所求二面角的平面角. ……………………………………………8分
在
中,由
,求得
.
.
即所求二面角的正切值为
. …………………………………………………12分
另解：（Ⅰ)建系设点正确2分,求出两个法向量2分,判断正确2分;
(Ⅱ)求出两个法向量3分,求出余弦值2分,求出正切值1分.
19. 解：（Ⅰ）设
,则
,
.
即点C的轨迹方程为
. …………………………………………………3分
（Ⅱ）
由题意
.
. ……………5分
.
,
. ……………………………8分
（Ⅲ）
.
.
.
∴双曲线实轴长的取值范围是
. ………………………………………………12分
20．解: (Ⅰ)由已知得的定义域为
,
. ………………2分
由题意得
对一切
恒成立,
……………………………………………5分
当时,
,
.故
.
…………………………………………7分
(Ⅱ)假设存在正实数,使得
成立.
.
…………………9分
由
,得
,
.由于
,故应舍去.
当
时,
………………………………………11分
令
,解得
或
. …………………………13分
另解: 假设存在正实数,使得成立.
设
,则
. ………………………9分
由
,解得
或
.
因为
,
在
上单调递增,在
上单调递减.
. … ……………………………………11分
令
,解得或. …………………………13分
21．解：（Ⅰ）由已知
，得
.
则数列
是公比为2的等比数列. ……………………………………………2分
又
. ……………………………………………4分
（Ⅱ）
. …………………6分
恒成立，则
解得
故存在常数A，B，C，满足条件. …………………………………………9分
（Ⅲ）由（Ⅱ）知：
. …………………14分
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com