|
试题详情
8.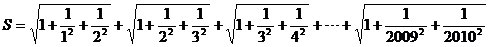 ,则不大于S的最大整数[S]等于 ( ) ,则不大于S的最大整数[S]等于 ( ) A.2008 B.2009 C.2010 D.2011 试题详情
二、填空题:本大题共7小题,每小题5分,共35分.将答案填在题中横线上. 9.在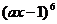 的二项展开式中,若中间项的系数是160,则实数a=
. 的二项展开式中,若中间项的系数是160,则实数a=
. 试题详情
10.现有同一型号的汽车50辆,为了了解这种汽车的每耗油1升所行路程的情况,要从中抽出5辆汽车做在同一条件下进行耗油1升所行路程的试验,得到如下数据(单位:km):11,15,9,12,13,则样本方差是
. 试题详情
11.一名高三学生希望报名参加某6所高校中的3所学校的自主招生考试,由于其中两所学校的考试时间相同,因此,该学生不能同时报考这两所学校,则不同的报名方法是
种(用数字作答). 试题详情
12.若正三棱柱的底面边长为3,侧棱长为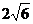 ,则该棱柱的外接球的表面积为
. ,则该棱柱的外接球的表面积为
. 试题详情
13.已知抛物线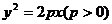 的焦点F恰好是椭圆 的焦点F恰好是椭圆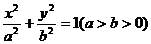 的右焦点,且两条曲线的公共点的连线过F,则该椭圆的离心率为 . 的右焦点,且两条曲线的公共点的连线过F,则该椭圆的离心率为 . 试题详情
14.已知函数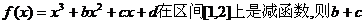 的最大值为 . 的最大值为 . 试题详情
15.定义在N上的函数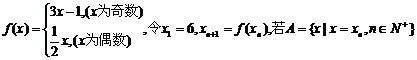 , , 则集合A的子集个数为
. 试题详情
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
试题详情
△ABC的三个内角分别为A、B、C,当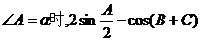 取得最大值. 取得最大值. 试题详情
(1)求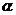 的值; 的值; (2)如果∠A的对边等于2,求△ABC的面积的最大值。 试题详情
试题详情
在一次人才招聘会上,小明同时参加了甲、乙、丙三家公司的招聘面试,小明在三家公司面试合格的概率分别为0.8,0.6,0.5.且在三家公司面试是否合格互不影响,求: (1)小明在三家公司至少有一家面试合格的概率; (2)小明在任意两家公司至少有一家面试合格的概率. 试题详情
18.(本小题满分12分) 如图在平行六面体ABCD―A1B1C1D1中,底面ABCD是矩形,AB=2,AD=1,顶点D1在底面ABCD上的射影O是CD的中点,侧棱与底面所成的角为60°. 试题详情

(2)求点O到平面AA1D1D的距离; (3)求二面角C―AD1―O的大小.
试题详情
试题详情
|
试题详情
(1)试写出 的值; 的值; 试题详情
(2)归纳出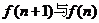 之间的关系式,并求出 之间的关系式,并求出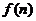 的表达式; 的表达式; 试题详情
(3)证明: 试题详情
试题详情
已知曲线 试题详情
(1)由曲线C上任一点E向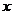 轴作垂线,垂足为F,动点P满足 轴作垂线,垂足为F,动点P满足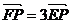 ,求P的轨迹方程,点P的轨迹可能是圆吗?请说明理由; ,求P的轨迹方程,点P的轨迹可能是圆吗?请说明理由; 试题详情
(2)如果直线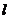 的斜率为 的斜率为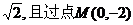 ,直线 ,直线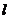 交曲线C于A、B两点,求 交曲线C于A、B两点,求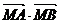 的取值范围. 的取值范围. 试题详情
试题详情
设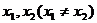 是函数 是函数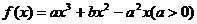 的两个极值点. 的两个极值点. 试题详情
(1)若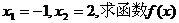 的解析式; 的解析式; 试题详情
(2)若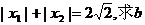 的最大值; 的最大值; 试题详情
(3)设函数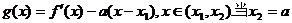 时,求证: 时,求证: 试题详情
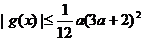 . .
试题详情
一、 ABCBA CDB 二、 9.―2 10.4 11.16 12.36 13. 13. 14. 15.64 15.64 三、 16.解:(1)  , ,
 …………………………2分 …………………………2分

 ………………4分 ………………4分

即 取得最大值为 取得最大值为 , ,  …………………………6分 …………………………6分
(2)设内角A、B、C的对边分别为a、b、c 由(1)知: 由余弦定理得:  ……………………8分 ……………………8分
 , ,
 当且仅当 12分 12分 17.解:记事件A、B、C分别表示小明在甲、乙、丙三家公司面试合格,则  (I)三家公司至少有一家面试合格的概率为:   在三家公司至少有一家面试合格的概率为0.96. 6分 在三家公司至少有一家面试合格的概率为0.96. 6分 (II)任两家公司至少有一家面试合格的概率等价于在三家公司至少有两家面试合格的概率,   8分 8分   在任意两家公司至少有一家面试合格的概率为0.7 12分 在任意两家公司至少有一家面试合格的概率为0.7 12分 18.解 :(I) D1在平面ABCD上的射影为O, D1在平面ABCD上的射影为O,

 2分 2分  点O为DC的中点,DC=2, 点O为DC的中点,DC=2,  OC=1. OC=1. 又 同理   平面D1AO. 4分 平面D1AO. 4分 (II) 平面ABCD, 平面ABCD,  又 平面D1DO. 平面D1DO.  , ,  , , 在平面D1DO内,作 垂足为H,则 平面ADD1A1 平面ADD1A1  线段OH的长为点O到平面ADD1A1的距离. 6分 线段OH的长为点O到平面ADD1A1的距离. 6分  平面ABCD, 平面ABCD,  在平面ABCD上的射影为DO. 在平面ABCD上的射影为DO.  为侧棱DD1与底面ABCD所成的角, 为侧棱DD1与底面ABCD所成的角,  在 即点O到平面ADD1A1的距离为 8分 8分

 平面ABCD, 平面ABCD,  又 平面AOD1, 平面AOD1, 又 , ,  为二面角C―AD1―O的平面角 10分 为二面角C―AD1―O的平面角 10分 在  在  取D1C的中点E,连结AE, 则   在 二面角C―AD1―O的大小为 12分
12分 19.解:(I)  3分 3分 (II)因为  归纳得 则 5分 5分    7分 7分 (III)当  9分 9分 则   13分 13分 20.解:(I)设    3分 3分 代入 为P点的轨
迹方程. 为P点的轨
迹方程. 当 时,P点的轨迹是圆. 6分 时,P点的轨迹是圆. 6分 (II)由题设知直线 的方程为 的方程为 , , 设 联立方程组 消去 8分 8分  方程组有两个不等解, 方程组有两个不等解,   而  10分 10分 当 当 当 综上, 13分
13分 21.解:(1)  1分 1分 依题意有  解得  4分 4分 (2) . . 依题意, 是方程 是方程 的两个根, 的两个根, 且     6分 6分 设 由 ; ; 由 所以函数 在区间 在区间 上是增函数,在区间[4,6]上是减函数. 上是增函数,在区间[4,6]上是减函数.  有极大值为96, 有极大值为96,  上的最大值为96. 上的最大值为96.  9分 9分 (III) 的两根, 的两根,  . .  ∴ = 11分
11分 ∵ < < < < 即 即 < < < < , ,  即   成立
13分 成立
13分
| | | | | | | | | 
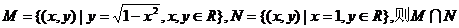 等于
等于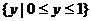 C.{1,0} D.
C.{1,0} D.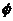
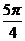 B.
B.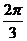 C.
C.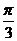 D.
D.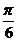
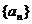 中,若
中,若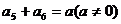 ,
,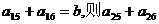 的值是( )
的值是( )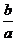 B.
B.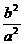 C.
C.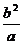 D.
D.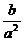
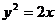 上,且与该抛物线的准线和x轴都相切的圆的方程是 ( )
上,且与该抛物线的准线和x轴都相切的圆的方程是 ( )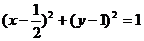 B.
B.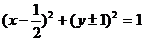
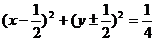 D.
D.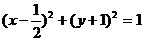
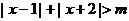 的解集为R;命题
的解集为R;命题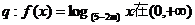 上为减函数,则p是q成立的 ( )
上为减函数,则p是q成立的 ( ) 在区间
在区间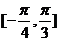 上的最小值为―2,则
上的最小值为―2,则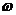 的取值范围是
的取值范围是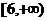 B.
B.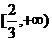 C.
C.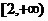 D.
D.