
2009届高考数学第三轮复习精编模拟十
参考公式:
如果事件 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么

 次独立重复试验中事件
次独立重复试验中事件 恰好发生
恰好发生 次的概率
其中
次的概率
其中 表示球的半径
表示球的半径

第一部分 选择题(共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1、设 其中i,j为互相垂直的单位向量,又
其中i,j为互相垂直的单位向量,又 ,则实数m =( )。w.w.w.k.s.5.u.c.o.m
,则实数m =( )。w.w.w.k.s.5.u.c.o.m
(A) 3 (B) 2 (C)-3 (D)-2
2、若 则下列结论中不正确的是 ( )w.w.w.k.s.5.u.c.o.m
则下列结论中不正确的是 ( )w.w.w.k.s.5.u.c.o.m
(A). ; (B)
; (B) 
 ;
;
(C). ; (D).
; (D).
3、方程 =
= 的实根有 ( )
的实根有 ( )
(A) 1个 (B) 2个 (C) 3个 (D) 无穷多个
4、过点(-1,3)且垂直于直线 的直线方程为 ( )
的直线方程为 ( )
A. ;B.
;B. ;C.
;C. ; D.
; D.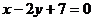
(A)(- ,-
,- ) (B)(-
) (B)(- ,0)
(C)(0,
,0)
(C)(0, ) (D)(
) (D)( ,
, )
)
6、已知复数z的模为2,则 |z-i| 的最大值为( )
A.1
B
7、已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2,则球面面积是( )
(A) π (B)
π (B) π (C)4π (D)
π (C)4π (D)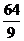 π
π
8、对任意θ∈(0,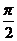 )都有( )
)都有( )
(A)sin(sinθ)<cosθ<cos(cosθ) (B) sin(sinθ)>cosθ>cos(cosθ)
(C)sin(cosθ)<cos(sinθ)<cosθ (D) sin(cosθ)<cosθ<cos(sinθ)
9、若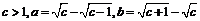 .则下列结论中正确的是 ( )
.则下列结论中正确的是 ( )




10、在坐标平面内,与点A(1,2)距离为1,且与点B(3,1)距离为2的直线共有 ( )
A、1条 B、2条 C、3条 D、4条
第二部分 非选择题(共100分)
二、填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
11、集合 的真子集的个数是
的真子集的个数是
12、如果函数 ,那么
,那么

13、 椭圆 上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
14、(坐标系与参数方程选做题) 设M、N分别是曲线 和
和 上的动点,则M、N的最小距离是
上的动点,则M、N的最小距离是
15.(几何证明选讲选做题)  如图,圆
如图,圆 是
是 的外接圆,过点C的切线交
的外接圆,过点C的切线交 的延长线于点
的延长线于点 ,
,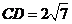 ,
, 。则
。则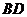 的长______________,
的长______________, 的长______________.
的长______________.
三.解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
设 是平面上的两个向量,且
是平面上的两个向量,且 互相垂直.
互相垂直.
(1)求λ的值;
(2)若 求
求 的值.
的值.
17.(本小题满分12分)
设 和
和 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量 表示方程
表示方程 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程 有实根的概率;
有实根的概率;
(Ⅱ)求 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程 有实根的概率.
有实根的概率.
18.(本小题满分14分)
已知三次函数 在
在 和
和 时取极值,且
时取极值,且 .
.
(Ⅰ) 求函数 的表达式;
的表达式;
(Ⅱ)求函数 的单调区间和极值;
的单调区间和极值;
(Ⅲ)若函数 在区间
在区间 上的值域为
上的值域为 ,试求
,试求 、
、 应满足的条件。
应满足的条件。
如图,在四棱锥 中,底面
中,底面 是正方形,
是正方形,
 底面
底面 ,
, , 点
, 点 是
是 的中点,
的中点,
 ,且交
,且交 于点
于点 .
.
(I) 求证:  平面
平面 ;
;
(II) 求二面角 的余弦值大小;
的余弦值大小;
(III)求证:平面 ⊥平面
⊥平面 .
.
20.(本小题满分14分)
双曲线M的中心在原点,并以椭圆 的焦点为焦点,以抛物线
的焦点为焦点,以抛物线 的准线为右准线.
的准线为右准线.
(Ⅰ)求双曲线M的方程;
(Ⅱ)设直线 :
: 与双曲线M相交于A、B两点,O是原点.
与双曲线M相交于A、B两点,O是原点.
① 当 为何值时,使得
为何值时,使得


 ?
?
② 是否存在这样的实数 ,使A、B两点关于直线
,使A、B两点关于直线 对称?若存在,求出
对称?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
21.(本小题满分14分)
把正奇数数列中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
― ― ― ―
― ― ― ― ―
设是位于这个三角形数表中从上往下数第行、从左往右数第个数。
(I)若,求的值;
(II)已知函数的反函数为 ,若记三角形数表中从上往下数第n行各数的和为,求数列的前n项和。

一.选择题:DDCAB DDDAB
解析:1: ∵
∵ ,
,
∴
∴ ,
,
而i,j为互相垂直的单位向量,故可得 ∴
∴ 。故选
。故选
2:∵ ∴0<b<a<1. 由指数函数的单调性可知:
∴0<b<a<1. 由指数函数的单调性可知: ,又∵
,又∵ ∴选(D)
∴选(D)
3:作y= 与y=
与y= 的图象,从图中可以看出:两曲线有3个交点,即方程有3个实根.选(C)
的图象,从图中可以看出:两曲线有3个交点,即方程有3个实根.选(C)
 |
4:由斜率去筛选,则可排除(C)、(D);再用点(-1,3)去筛选,代入(A)成立,
∴应选(A).
5:取α= ± 、±
、± ,代入求出sinα、tanα
、cotα 的值,易知α=-
,代入求出sinα、tanα
、cotα 的值,易知α=- 适合题设条件,∴应选(B).
适合题设条件,∴应选(B).

M - i
2 


6:由复数模的几何意义,画出右图,可知当圆上的点到M的距离最大时即为|z-i|最大。所以选D
7: ∵球的半径R不小于△ABC的外接圆半径r= , 则S球=4πR2≥4πr2=
, 则S球=4πR2≥4πr2= π>5π,故选(D).
π>5π,故选(D).
8:当θ 0时,sin(sinθ)
0时,sin(sinθ) 0,cosθ
0,cosθ 1,cos(cosθ)
1,cos(cosθ) cos1,故排除A,B.
cos1,故排除A,B.
当θ
 时,cos(sinθ)
时,cos(sinθ) cos1,cosθ
cos1,cosθ 0,故排除C,因此选D.
0,故排除C,因此选D.
9:由于 的含义是
的含义是 于是若
于是若 成立,则有
成立,则有 成立;同理,若
成立;同理,若 成立,则
成立,则 也成立,以上与指令“供选择的答案中只有一个正确”相矛盾,故排除
也成立,以上与指令“供选择的答案中只有一个正确”相矛盾,故排除 .再考虑
.再考虑 ,取
,取 代入得
代入得 ,显然
,显然 ,排除
,排除 .故选
.故选 .
.
10:选项暗示我们,只要判断出直线的条数就行,无须具体求出直线方程。以A(1,2)为圆心,1为半径作圆A,以B(3,1)为圆心,2为半径作圆B。由平面几何知识易知,满足题意的直线是两圆的公切线,而两圆的位置关系是相交,只有两条公切线。故选B。
二.填空题:11、 ;12、
;12、 ; 13、
; 13、 或
或 ;14、-1;15、4,
;14、-1;15、4, ;
;
解析:
11:  ,显然集合M中有90个元素,其真子集的个数是
,显然集合M中有90个元素,其真子集的个数是 ,应填
,应填 .
.
12:容易发现 ,于是 原式=
,于是 原式= ,应填
,应填
13:记椭圆的二焦点为 ,有
,有
则知
显然当 ,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
故应填 或
或
14.(略)
15.(略)
三.解答题:
16.解:(1)由题设,得
 -----------------3分
-----------------3分
因为 与
与 垂直
垂直  即
即
 . 又
. 又 ,故
,故 ,∴
,∴ 的值为2. ------------------6分
的值为2. ------------------6分
(2)当 垂直时,
垂直时,
 ------------------8分
------------------8分
 ,则
,则 ------------------10分
------------------10分
 ------------------12分
------------------12分
17.解:(I)基本事件总数为 ,
,
若使方程有实根,则 ,即
,即 。------------------2分
。------------------2分
当 时,
时, ; 当
; 当 时,
时, ; ------------------3分
; ------------------3分
当 时,
时, ; 当
; 当 时,
时, ; ------------------4分
; ------------------4分
当 时,
时, ; 当
; 当 时,
时, , ------------------5分
, ------------------5分
目标事件个数为
因此方程 有实根的概率为
有实根的概率为 ------------------6分
------------------6分
(II)由题意知, ,则
,则
 ,
,
 ,
,
故 的分布列为
的分布列为

0
1
2
P



 的数学期望
的数学期望 ------------------10分
------------------10分
(III)记“先后两次出现的点数中有 有实根” 为事件N,则
有实根” 为事件N,则 ,
, ,
,  .------------------12分
.------------------12分

18.解:(Ⅰ) ,
,
由题意得, 是
是 的两个根,
的两个根,
解得, . ------------------2分
. ------------------2分
再由 可得
可得 .
.
∴ . ------------------4分
. ------------------4分
(Ⅱ) ,
,
当 时,
时, ;当
;当 时,
时, ;------------------5分
;------------------5分
当 时,
时, ;当
;当 时,
时, ;------------------6分
;------------------6分
当 时,
时, .∴函数
.∴函数 在区间
在区间 上是增函数;------------------7分
上是增函数;------------------7分
在区间 上是减函数;在区间
上是减函数;在区间 上是增函数.
上是增函数.
函数 的极大值是
的极大值是 ,极小值是
,极小值是 . ------------------9分
. ------------------9分
(Ⅲ)函数 的图象是由
的图象是由 的图象向右平移
的图象向右平移 个单位,向上平移4
个单位,向上平移4 个单位得到,
个单位得到,
所以,函数 在区间
在区间 上的值域为
上的值域为 (
( ).-------------10分
).-------------10分
而 ,∴
,∴ ,即
,即 .
.
于是,函数 在区间
在区间 上的值域为
上的值域为 .------------------12分
.------------------12分
令 得
得 或
或 .
.
由 的单调性知,
的单调性知, ,即
,即 .
.
综上所述, 、
、 应满足的条件是:
应满足的条件是: ,且
,且 ------------------14分
------------------14分
19.(Ⅰ)证明:连结 交
交 于
于 ,连结
,连结 .
.
 是正方形,∴
是正方形,∴  是
是 的中点. ----------1分
的中点. ----------1分
 是
是 的中点, ∴
的中点, ∴ 是
是 的中位线. ∴
的中位线. ∴ . ----------2分
. ----------2分
又∵ 平面
平面 ,
, 
 平面
平面 , ----------3分
, ----------3分
∴
 平面
平面 .------------------4分
.------------------4分
(II)如图,以A为坐标原点,建立空间直角坐标系 ,
,
由 故设
故设 ,则
,则

 . ----------6分
. ----------6分

 底面
底面 ,
,
∴ 是平面
是平面 的法向量,
的法向量, .----------7分
.----------7分
设平面 的法向量为
的法向量为 ,
,
 ,
,
则 即
即
∴  令
令 ,则
,则 . ----------9分
. ----------9分
∴ ,
,
∴二面角 的余弦值为
的余弦值为 . ------------------10分
. ------------------10分
(III)
 ,
,  ,
,
 ----------11分
----------11分
 又
又 且
且 .----------12分
.----------12分
 . 又
. 又 平面
平面 ----------13分
----------13分
∴平面 ⊥平面
⊥平面 . ------------------14分
. ------------------14分
20.解:(Ⅰ)易知,椭圆 的半焦距为:
的半焦距为: ,
,
又抛物线 的准线为:
的准线为: . ----------2分
. ----------2分
设双曲线M的方程为 ,依题意有
,依题意有 ,
,
故 ,又
,又 .
.
∴双曲线M的方程为 . ----------4分
. ----------4分
(Ⅱ)设直线 与双曲线M的交点为
与双曲线M的交点为 、
、 两点
两点
联立方程组 消去y得
消去y得  ,-------5分
,-------5分
∵ 、
、 两点的横坐标是上述方程的两个不同实根, ∴
两点的横坐标是上述方程的两个不同实根, ∴
∴
 ,
,
从而有 ,
, . ----------7分
. ----------7分
又 ,
,
∴ .
.
①
若


 ,则有
,则有
 ,即
,即
 .
.
∴当 时,使得
时,使得


 . ----------10分
. ----------10分
② 若存在实数 ,使A、B两点关于直线
,使A、B两点关于直线 对称,则必有
对称,则必有  ,
,
因此,当m=0时,不存在满足条件的k;
当 时,由
时,由 得
得 



∵A、B中点 在直线
在直线 上,
上,
∴ ,代入上式得
,代入上式得
 ,又
,又 , ∴
, ∴ ----------13分
----------13分
将 代入并注意到
代入并注意到 ,得
,得
 .
.
∴当 时,存在实数
时,存在实数 ,使A、B两点关于直线
,使A、B两点关于直线 对称----------14分
对称----------14分
21.解(I)三角形数表中前行共有个数,
第行最后一个数应当是所给奇数列中的第项。
故第行最后一个数是
因此,使得的m是不等式的最小正整数解。----------4分
由得
----------6分
于是,第45行第一个数是
----------7分
(II),。
故 ----------9分
第n行最后一个数是,且有n个数,若将看成第n行第一个数,则第n行各数成公差为-2的等差数列,故。
故
,
两式相减得:
----------13分
----------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com