
2009届高考数学第三轮复习精编模拟八
参考公式:
如果事件 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么

 次独立重复试验中事件
次独立重复试验中事件 恰好发生
恰好发生 次的概率
其中
次的概率
其中 表示球的半径
表示球的半径

第一部分 选择题(共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1、如果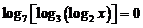 ,那么
,那么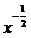 等于( )w.w.w.k.s.5.u.c.o.m
等于( )w.w.w.k.s.5.u.c.o.m
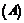
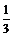
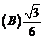
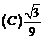
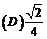
2 已知
已知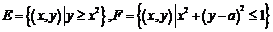 ,那么使
,那么使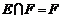 成立的充要条件是
( )
成立的充要条件是
( )
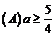
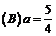
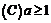
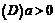
3、设f(x)是(-∞,∞)是的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7.5)等于( )
(A) 0.5 (B) -0.5 (C) 1.5 (D) -1.5
4、若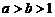 ,P=
,P=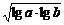 ,Q=
,Q=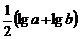 ,R=
,R=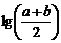 ,则( )
,则( )
(A)R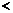 P
P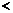 Q
(B)P
Q
(B)P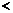 Q
Q 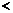 R
R
(C)Q 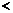 P
P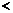 R
(D)P
R
(D)P 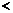 R
R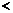 Q
Q
 5、函数y=sin(
5、函数y=sin(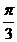 -2x)+sin2x的最小正周期是(
)w.w.w.k.s.5.u.c.o.m
-2x)+sin2x的最小正周期是(
)w.w.w.k.s.5.u.c.o.m
(A)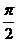 (B)
(B) 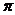 (C) 2
(C) 2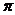 (D) 4
(D) 4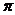
6、在圆x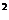 +y
+y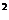 =4上与直线4x+3y-12=0距离最小的点的坐标是( )
=4上与直线4x+3y-12=0距离最小的点的坐标是( )
(A)(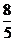 ,
,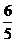 )
(B)(
)
(B)(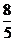 ,-
,-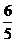 )
)
(C)(-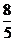 ,
,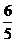 )
(D)(-
)
(D)(-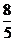 ,-
,-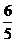 )
)
7、不等式组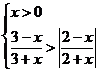 的解集是( )
的解集是( )
(A)(0,2) (B)(0,2.5) (C)(0,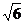 ) (D)(0,3)
) (D)(0,3)
8、在正n棱锥中,相邻两侧面所成的二面角的取值范围是( )
(A)(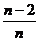 π,π)
(B)(
π,π)
(B)(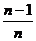 π,π)
π,π)
(C)(0,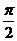 )
(D)(
)
(D)(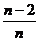 π,
π,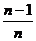 π)
π)
9、定义在区间(-∞,+∞)的奇函数f(x)为增函数;偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合,设 a>b>0 ,给出下列不等式:
① f(b)-f(-a)>g(a)-g(-b) ② f(b)-f(-a)<g(a)-g(-b)
③ f(a)-f(-b)>g(b)-g(-a) ④f(a)-f(-b)<g(b)-g(-a)
其中成立的是 ( )
(A)①与④ (B)②与③ (C)①与③ (D)②与④
10、若过定点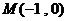 且斜率为
且斜率为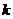 的直线与圆
的直线与圆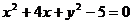 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则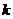 的取值范围是( )
的取值范围是( )
A. 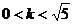 B.
B. 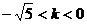 C.
C. 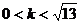 D.
D. 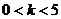
第二部分 非选择题(共100分)
二、填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
11、如果不等式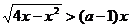 的解集为A,且
的解集为A,且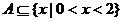 ,那么实数a的取值范围是
。
,那么实数a的取值范围是
。
12、设复数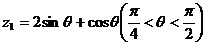 在复平面上对应向量
在复平面上对应向量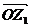 ,
, 将
将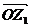 按顺时
按顺时
针方向旋转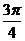 后得到向量
后得到向量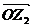 ,
,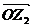 对应的复数为
对应的复数为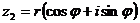 ,则
,则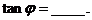
13、某商场开展促销活动,设计一种对奖券,号码从000000到999999. 若号码的奇位数字是不同的奇数,偶位数字均为偶数时,为中奖号码,则中奖面(即中奖号码占全部号码的百分比)为 .
 14、(坐标系与参数方程选做题) 极坐标方程
14、(坐标系与参数方程选做题) 极坐标方程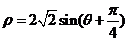 所表示的曲线的直角坐标方程是
。
所表示的曲线的直角坐标方程是
。
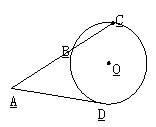
15.(几何证明选讲选做题) 已知圆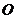 的半径为
的半径为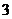 ,从圆
,从圆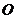 外一点
外一点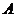 引切线
引切线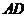 和割线
和割线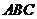 ,圆心
,圆心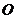 到
到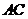 的距离为
的距离为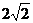 ,
,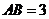 ,则切线
,则切线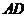 的长为 _____。
的长为 _____。
三.解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
已知: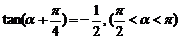 。
。
(1)求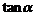 的值;
的值;
(2)求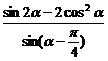 的值。
的值。
17.(本小题满分12分)
一种电脑屏幕保护画面,只有符号“○”和“×”随机地反复出现,每秒钟变化一次,每次变
化只出现“○”和“×”之一,其中出现“○”的概率为p,出现“×”的概率为q,若第k次
出现“○”,则记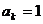 ;出现“×”,则记
;出现“×”,则记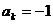 ,令
,令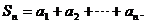
(I)当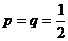 时,记
时,记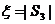 ,求
,求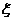 的分布列及数学期望;
的分布列及数学期望;
(II)当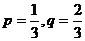 时,求
时,求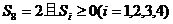 的概率.
的概率.
18.(本小题满分14分)
已知:函数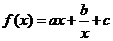 (
(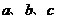 是常数)是奇函数,且满足
是常数)是奇函数,且满足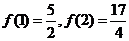 ,
,
(Ⅰ)求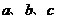 的值;
的值;
(Ⅱ)试判断函数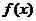 在区间
在区间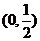 上的单调性并说明理由;
上的单调性并说明理由;
(Ⅲ)试求函数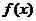 在区间
在区间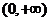 上的最小值.
上的最小值.
19.(本小题满分14分)
 如图,已知正三棱柱
如图,已知正三棱柱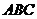 ―
―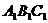 的底面边长是
的底面边长是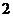 ,
,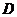 是侧棱
是侧棱 的中点,直线
的中点,直线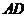 与侧面
与侧面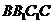 所成的角为
所成的角为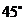 .
.
(Ⅰ)求此正三棱柱的侧棱长;
(Ⅱ) 求二面角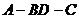 的大小;
的大小;
(Ⅲ)求点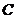 到平面
到平面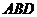 的距离.
的距离.
20.(本小题满分14分)
设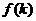 是满足不等式
是满足不等式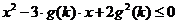 的自然数
的自然数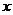 的个数,其中
的个数,其中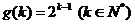 .
.
(Ⅰ)求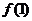 的值;
的值;
(Ⅱ) 求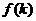 的解析式;
的解析式;
(Ⅲ)记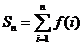 ,令
,令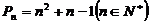 ,试比较
,试比较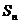 与
与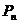 的大小.
的大小.
21.(本小题满分14分)
|