2009届山东省枣庄市高三第一学期期末检测试卷
数学(文科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。满分150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x|x2-3x―4>0},B={x||x-3|>4},则 为 ( )
为 ( )
试题详情
A. B.
B.
试题详情
C. D.[―1,7]
D.[―1,7]
试题详情
2.在等差数列 等于 ( )
等于 ( )
A.55 B.40 C.35 D.70
试题详情
3.函数 的零点所在的区间是 ( )
的零点所在的区间是 ( )
A.(0,1) B.(1,10) C.(10,100) D.(100,+∞)
试题详情
4.两个正数a、b的等差中项是 ,一个等比中项是
,一个等比中项是 的离心率e等于 ( )
的离心率e等于 ( )
试题详情
试题详情
5.已知 的值等于 ( )
的值等于 ( )
试题详情
试题详情
6.设 为 ( )
为 ( )
A.15° B.30° C.45° D.60°
试题详情
7.如图几何体的主(正)视图和左(侧)视图都正确的是 ( )
试题详情
|
试题详情
8.已知圆 的取值范围 ( ) 的取值范围 ( ) 试题详情
试题详情
9.已知m,n是不重合的直线, 是不重合的平面,给出下列命题: 是不重合的平面,给出下列命题: 试题详情
①若 ; ; 试题详情
②若 ; ; 试题详情
③如果 是异面直线,则 是异面直线,则 相交; 相交; 试题详情
④若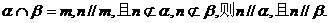 其中正确命题的个数是 ( ) A.1 B.2 C.3 D.4 试题详情
10.已知a、 那么“ 那么“ ”是“ ”是“ ”的 ( ) ”的 ( ) A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条件 试题详情
试题详情
 的值域为 ( ) 的值域为 ( )
试题详情
试题详情
12.定义在R上的函数 单调递增,如果 单调递增,如果 试题详情
 的值 ( ) 的值 ( ) A.恒小于0 B.恒大于0 C.可能为0 D.可正可负 第Ⅱ卷(非选择题,共90分) 试题详情
二、填空题:本大题共4小题,每小题4分,共16分。把答案写在题中的横线上。 13.抛物线 上的两点A、B到焦点的距离之和是5,则线段AB中点到y轴的距离是
。 上的两点A、B到焦点的距离之和是5,则线段AB中点到y轴的距离是
。 试题详情
14.已知函数 的值为
。 的值为
。 试题详情
15.已知变量 (其中a>0)仅在点(3,0)处取得最大值,则a的取值范围为
。 (其中a>0)仅在点(3,0)处取得最大值,则a的取值范围为
。 试题详情
试题详情
试题详情
②已知直线l1: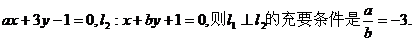 试题详情
③命题“若 ”的逆否命题为:“若 ”的逆否命题为:“若 ”。其中正确结论的序号为
。(把你认为正确的命题序号都填上) ”。其中正确结论的序号为
。(把你认为正确的命题序号都填上) 试题详情
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
试题详情
试题详情
(I)求函数 的表达式; 的表达式; 试题详情
(II)在△ABC,若 的值。 的值。 试题详情
试题详情
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆。本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应提高的比例为0.7x,年销售量也相应增加。已知年利润=(每辆车的出厂价―每辆车的投入成本)×年销售量。 试题详情
(I)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内? 试题详情
(II)年销售量关于x的函数为 为何值时,本年度的年利润最大?最大利润为多少? 为何值时,本年度的年利润最大?最大利润为多少? 试题详情
19.(本小题满分12分) 如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F 是CD的中点。 (I)求证:AF//平面BCE; (II)求证:平面BCE⊥平面CDE; 试题详情
|
|
|
试题详情
试题详情
已知数列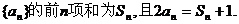 试题详情
(I)求数列 的通项公式; 的通项公式; 试题详情
(II)设Tn为数列 ,求m的最小值。 ,求m的最小值。 试题详情
试题详情
在实数集R上定义运算: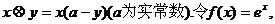 试题详情
试题详情
(I)求 的解析式; 的解析式; 试题详情
(II)若函数 处的切线斜率为―3,求此切线方程; 处的切线斜率为―3,求此切线方程; 试题详情
(III)若函数 的单调区间。 的单调区间。 试题详情
22.(本小题满分14分) 如图所示,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过 试题详情
点M(2,1)。平行于OM的直线l在y轴上的截距为 ,且交椭圆于A,B两点。 ,且交椭圆于A,B两点。 (I)求椭圆的方程; (II)求M的取值范围; (III)求证:直线MA、MB与x轴围成一个等腰三角形。 试题详情
|
|
|
试题详情
一、选择题:本大题共12小题,每小题5分,共60分。 ABBD DBBA BCBA 二、填空题:本大题共4小题,每小题4分,共16分。 13.2 14.3 15. 16.①③ 16.①③ 三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。 17.解:(I) ………2分 ………2分 依题意函数 所以 …………4分 …………4分  (II)  18.解:(I)由题意得:上年度的利润的 万元; 万元; 本年度每辆车的投入成本为 万元; 万元; 本年度每辆车的出厂价为 万元; 万元; 本年度年销售量为 ………………2分 ………………2分 因此本年度的利润为  (II)本年度的利润为  ………………7分 则 由 (舍去)。 …………9分 (舍去)。 …………9分

19.(I)解:取CE中点P,连结FP、BP, ∵F为CD的中点, ∴FP//DE,且FP= …………2分 …………2分 又AB//DE,且AB= ∴AB//FP,且AB=FP, ∴ABPF为平行四边形,∴AF//BP。…………4分 又∵AF 平面BCE,BP 平面BCE,BP 平面BCE, 平面BCE, ∴AF//平面BCE。 …………6分 (II)∵△ACD为正三角形,∴AF⊥CD。 ∵AB⊥平面ACD,DE//AB, ∴DE⊥平面ACD,又AF 平面ACD, 平面ACD, ∴DE⊥AF。又AF⊥CD,CD∩DE=D,
…………9分 ∴AF⊥平面CDE。 又BP//AF,∴BP⊥平面CDE。又∵BP 平面BCE, 平面BCE, ∴平面BCE⊥平面CDE。 …………12分 20.解:(I)由题意知 
(II)
 
 的最小值为10。 …………12分 的最小值为10。 …………12分
21.解:(I) …………1分 …………1分 (II) 由条件得 …………3分 …………3分 而 …………4分 …………4分 (III)由(II)知 ①当 时, 时, 
②当 时, 时, 
③当 时, 时, 
综上所述:当 单调减区间为 单调减区间为 单调增区间为 单调增区间为  …………12分 …………12分
22.解:(I)设椭圆的方程为 则 …………4分 …………4分 (II) 由 …………6分 …………6分  交椭圆于A,B两点, 交椭圆于A,B两点,
 …………8分 …………8分
(3)设直线MA、MB的斜率分别为k1,k2,则问题只需证明 
 、MB与x轴围成一个等腰三角形。 …………14分 、MB与x轴围成一个等腰三角形。 …………14分
| | | | | | | |

 为 ( )
为 ( ) B.
B.
 D.[―1,7]
D.[―1,7] 等于 ( )
等于 ( ) 的零点所在的区间是 ( )
的零点所在的区间是 ( ) ,一个等比中项是
,一个等比中项是 的离心率e等于 ( )
的离心率e等于 ( ) B.
B. C.
C. D.
D.
 的值等于 ( )
的值等于 ( ) B.
B. C.―
C.― D.―
D.―
 为 ( )
为 ( )