
【教学目标】
三、情感态度和价值观:体会实际需求与数学内部的矛盾(数的运算规则、方程求根)在数系扩充过程中的作用,感受人类理性思维的作用以及数与现实世界的联系.
1.对数集因生产和科学发展的需要而逐步扩充的过程进行概括(教师引导学生进行简明扼要的概括和总结)自然数 →整数→有理数→无理数→实数
相关链接:数的发展里程
2.提出问题
我们知道,对于实系数一元二次方程 ,没有实数根.我们能否将实数集进行扩充,使得在新的数集中,该问题能得到圆满解决呢?
,没有实数根.我们能否将实数集进行扩充,使得在新的数集中,该问题能得到圆满解决呢?
3.组织讨论,研究问题
我们说,实系数一元二次方程 没有实数根.实际上,就是在实数范围内,没有一个实数的平方会等于负数.解决这一问题,其本质就是解决一个什么问题呢?(最根本的问题就是要解决-1的开平方问题.即一个什么样的数,它的平方会等于-1.)
没有实数根.实际上,就是在实数范围内,没有一个实数的平方会等于负数.解决这一问题,其本质就是解决一个什么问题呢?(最根本的问题就是要解决-1的开平方问题.即一个什么样的数,它的平方会等于-1.)
二、新课内容:
引入新数 ,并给出它的两条性质
,并给出它的两条性质
根据前面讨论的结果,我们引入一个新数 ,
, 叫做虚数单位,并规定:
叫做虚数单位,并规定:
(1) ;
;
(2)实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立.
有了前面的讨论,引入新数 ,可以说是水到渠成的事.这样,就可以解决前面提出的问题(-1可以开平方,而且-1的平方根是
,可以说是水到渠成的事.这样,就可以解决前面提出的问题(-1可以开平方,而且-1的平方根是 ).
).
1.提出复数的概念
根据虚数单位 的第(2)条性质,
的第(2)条性质, 可以与实数b相乘,再与实数a相加.由于满足乘法交换律及加法交换律,从而可以把结果写成
可以与实数b相乘,再与实数a相加.由于满足乘法交换律及加法交换律,从而可以把结果写成 这样,数的范围又扩充了,出现了形如
这样,数的范围又扩充了,出现了形如
 的数,我们把它们叫做复数.其中a叫做这个复数的实部,b叫做虚部
的数,我们把它们叫做复数.其中a叫做这个复数的实部,b叫做虚部
全体复数所形成的集合叫做复数集,一般用字母C表示,显然有:
(1)N* N
N Z
Z Q
Q R
R C.(2)复数a+bi(a,b为实数)
C.(2)复数a+bi(a,b为实数)
巩固练习:
例1、下列数中,哪些是实数,哪些是虚数,哪些是纯虚数?并分别指出这些复数的实部与虚部各是什么?4,2-3i,0,- +
+ ,5+
,5+ ,6i(教材P104例1)
,6i(教材P104例1)
练习、判断下列命题是否正确:
(1)若a、b为实数,则Z=a+bi为虚数
(2)若b为实数,则Z=bi必为纯虚数
(3)若a为实数,则Z= a一定不是虚数
例2、 实数m分别取什么值时,复数z=m(m-1)+(m-1)i是(1)实数?(2)虚数?(3)纯虚数? (教材P104例2)
练习:实数m分别取什么值时,复数z=m2+m-2+(m2-1)i是(1)实数?(2)虚数?(3)纯虚数?
2.提出两个复数相等的定义,即两个复数相等的充要条件是它们的实部与虚部分别对应相等.也就是

由此容易得出:
例3、 已知x+y+(x-2y)i=2x-5+(3x+y)i,求实数x与y.
分析:因为x,y∈R,所以由两个复数相等的定义,可列出关于x,y的方程组,解这个方程组,可求出x,y的值.
练习:教材P105---练习4
思考:两个复数若不全是实数,能否比较大小?
最简单的虚数单位i和0的大小如何?(若i>0,则i2>0,-1>0不成立;若i<0,则i2>0,-1>0不成立。这样两个复数只要不全是实数,就不能比较大小。)
例4、对于实数x,是否存在实数a,使3x2+(x-a+1)2i>27+(x2+a-ax-1)i,若存在,求出a的范围集合;否则说明理由
解:x-a+1=0=x2+a-ax-1,且3x2>27, a<-2或a>4
三、归纳总结
(1)、虚数单位i的引入;
(2)、复数的代数形式: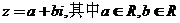 ;
;
(2)、复数的有关概念:虚数,纯虚数,实部、虚部、复数相等。
[补充习题]
四、布置作业:P105----习题1~4
1、复数z=sin2x-i(1-cos2x)是纯虚数,则实数x=____________
2、设z=log2(m2
3、关于x的方程x2-(2i-1)x+2p-i=0有实数根,求实数p的值或范围
[答案]
1、kπ+ ,k∈Z
,k∈Z
2、(4, )
)
3、p=1/8
备课资料:
数系的发展历程
数的概念是从生活、生产、科研等社会实践中发展起来的,每一种数的发展均有两个方向:一是其内涵的增容、规范及应用的日臻完善的纵向过程,二是对其出现的不可调和的矛盾而衍生新数的横向发展,在这种纵横交错中,数一步步走向系统完整。
一,正整数在勇往直前中成熟
人类最初只有“无”与“有”这两个描写一天有无猎物或是否见到同伴的词。后来,从“有”中分化出“多”与“少”等模糊的量词。由于具体记数的需要,人们开始用自己的手指,伸出一个手指去说明有一只兔子或抓住一只羔羊,正整数1就这样诞生了,由1而有2、3、4……;为了表示更多的数,人们借助于用具来体现,由于用具选择的不同,体现的规则也不尽相同,从而形成不同的位值数,如:我国以手指记数,指头至十完结,十之后借助于绳子打结,形成“结绳记数”的十进制规则,后逐渐以“结绳”与手指共同记数,成为世界上最早采用十进制的国家;古希腊则“以石记数”,沿用古巴比伦的六十进位制;而中美洲的马雅人采用二十进位制,等。
现在国际上记数符号――数字,为阿拉伯数字,实质是文字诞生较早的印度首先发明和使用的,后传入阿拉伯,十三世纪才由欧洲人将之译成拉丁文而传入欧洲。所以,在欧洲人看来,数字来自阿拉伯而称阿拉伯数字,但在译制过程中,不同时代随社会文明的进步,代码及符号又不尽相同。至1522年,英国的Tonstall所写的书中,才形成现在这种数字写法。
这样,加上一些运算规则,形成了正整数体系的雏形,系统的定义则是在公理化思想、集合概念都出现后,由意大利的Peano于1891年在他的论文《关于数的概念》中提出的,称自然数公理(Peano说的自然数即正整数,不含数字0),其要点是五条公理:①1是自然数;②1不是任何其他自然数的直接后继者;③每个自然数a都有一个后继者;④若a 的后继者与b的后继者相等,则a与b相等;⑤若一个自然数组成的集合S含有1,又若当S含有任意数a时,它一定含有a的后继者,则S含有全体自然数。这样,正整数才真正走到成熟。
二,分数、负数、零的引入,使数在纤纤细步的增容中完成量变的积累
随社会的发展,分配及更精确丈量土地的需要,正整数已不够用,人们引进了分数。世界上最早有关分数的记载,要数埃及的纸草文书,但迟至公元前1650年的Ahmes所著的《获得一切奥秘的指南》,仍将分数化成分子是1再加以计算;我国在公元前100年的《周髀算经》中就有了具体分数的计算,在其后的《孙子算经》及《九章算术》中就明确总结了分数的计算、表示方法,(只不过当时分数的表示方法是分子在上、分母在下、中间无横线,且带分数的整数部分又排在最上面)。现今的分数表示法 ,迟至1175年中亚西亚的Al-Hassan才在其著作中出现,同时十进制分数西传过程中与印度文化相结合,如:叙利亚的Al-Battanl于十世纪引入正切、余切时采用了小数,使分数在编译过程中改进为另一面貌形式。
,迟至1175年中亚西亚的Al-Hassan才在其著作中出现,同时十进制分数西传过程中与印度文化相结合,如:叙利亚的Al-Battanl于十世纪引入正切、余切时采用了小数,使分数在编译过程中改进为另一面貌形式。
负数及运算法则也是我国最先引入的:在《九章算术》中,以收入、余钱、入帐为正,付款、不足、减掉为负,并系统阐述了加减的运算法则,因该书是对前人经验的总结,因此实质负数及其运算规则比它要早些;至1299年,朱世杰编的《算学启蒙》中有了负数乘除法的法则。欧洲对负数的处理是由意大利的Fibonacci提出后又不敢承认,一段时间内将之视作“假数”或“荒诞的数”,至Bcmbell才给出明确的定义,Girdrd将负数与正数等量齐观,并用“-”表示负数,一直沿用至今。
三,跌宕起伏的无理数
远在公元前500年左右,古希腊著名的Pythagores学派就认为:“万物皆数,数皆可归为整数或整数之比,此比称公度比”,即现在的正有理数(因当时欧洲还没有负数及零的概念);但在公元前五世纪时,该学派的一名成员Hippasus发现:“正方形的对角线与其一边无公度比”,这一发现使该学派成员大为惊慌――居然有人敢反对伟大的Pythagores!在争论和大家的愤怒声讨中,犯了众怒的Hippasus被抛入大海。
另一方面,为表示“没有”的意思而引入数字零。现今发现的文献中,最早有零的是公元前600年的巴比伦泥版文书,只不过当时零用空格表示,且仅仅作为一个记号,并没有引入计算。对零引入计算的要数印度人为先:约在三、四世纪,他们就用“?”表示零,并加以计算应用,但总结出“一数乘零得零,一数加零、减零不变”的计算的规律则在9世纪末Mahavira的《计算精要》文献中。至于现在的零写法“0”,以公元初印第安人马雅族用贝壳的图形符号“O”(俗称蝌蚪文)为早。无论如何,零的加入,使位值制得以真正完善。
 Pythagores
Pythagores  Descartes
Descartes
Hippasus虽然死了,但他的“无公度比”的观念并没有随之消亡。Plato学派的前驱Theodorus又证明了 、
、 、
、 也没有公度比,可惜这一学派又不愿接受无理数这一新概念。之后的Eudoxus及Euclid是通过“量”概念的引入,用几何方法处理这种“无公度比”(用现在的话说,就是找近似的有理数来代替这个数),这又基本上将无理数抹杀。在东方的印度,也同样在十二世纪仍将无理数当作有理数加以处理。直至十九世纪的1872年,德国的Dedekind才将之分离出来,为区分以往的数而命名为无理数,将原有的可以化为整数比的数称有理数,并将无理数与有理数统称实数,创建了实数理论;之后的1874年,德国的Cator验证了Dedekind理论的正确性,并证明了“实数与数轴上点一一对应”的理论,至此,完成了真正意义上的实数理论。
也没有公度比,可惜这一学派又不愿接受无理数这一新概念。之后的Eudoxus及Euclid是通过“量”概念的引入,用几何方法处理这种“无公度比”(用现在的话说,就是找近似的有理数来代替这个数),这又基本上将无理数抹杀。在东方的印度,也同样在十二世纪仍将无理数当作有理数加以处理。直至十九世纪的1872年,德国的Dedekind才将之分离出来,为区分以往的数而命名为无理数,将原有的可以化为整数比的数称有理数,并将无理数与有理数统称实数,创建了实数理论;之后的1874年,德国的Cator验证了Dedekind理论的正确性,并证明了“实数与数轴上点一一对应”的理论,至此,完成了真正意义上的实数理论。
四,无聊游戏中出现的复数
人们最早在研究方程时,认为x2+1=0之类的方程必定无解,由于习惯用历史来解释现实与告诉未来,所以人们也就习惯地将“其有解”视作是永不可能的。1545年,意大利的Cardano在其著作《大术》中讨论了这样的问题:“是否可以将十分成二部分,使它们的积等于40”,用现在的话即解方程x2-10x+40=0,他大胆提出了两个解5± (只不过当时不这样记),Cardano将之称作“诡辩量”,既然是诡辩量,自然在当时也将之视作一种无聊的游戏(它标志着虚数的诞生),正是这一游戏,27年后,意大利的Bembeli在其《代数学》中,用之完整地得到了一元三次方程的求根公式。
(只不过当时不这样记),Cardano将之称作“诡辩量”,既然是诡辩量,自然在当时也将之视作一种无聊的游戏(它标志着虚数的诞生),正是这一游戏,27年后,意大利的Bembeli在其《代数学》中,用之完整地得到了一元三次方程的求根公式。
但,人们的观念并没有随之带来变化。如:Descartes在1637年的《几何学》中,认为它非实在,故起名为imaginary number(虚数)!大科学家Newton也不承认它,继续把它当作一种无聊的游戏;Leibniz更是发扬这一传统思想,称:虚数是介于存在与不存在间的无聊的两栖物。
至1747年,法国的D/Alembert才将虚数与实数并列看待,并将实数与虚数统称为数(当时的实数实质指的是有理数);1777年,瑞士的Euler系统地建立了复数理论,并首次用i表示虚数单位,发现了复指数函数与三角函数间关系;至1801年,德国的Guass系统地使用了i这个记号及运算法则,将实数与虚数统称复数,并将复数与几何建立了对应关系,复数理论走向了应用。
五,计算机的问世,使“二进制”这一古文明复活
自然界中存在着大量截然相反的状态,如:有与无、大与小、高与底、通与断,既然用十个手指可以用来表示十进制数,那么用两手或两脚也可以记数,这样就形成了二进制记数法。在我国周朝的《易经》中就记载了用不断的横“―”和断开的横“--”表示两种相反的状态,如果将“―”记作现在的1,而“--”视作现在的0,其实就形成了现在的二进制,根据各种文献考证,这一符号诞生于原始社会伏羲时代的“八卦”。但由于二进制表示数很冗长,人们并没有在数学中引起重视,在我国,它却成为算命的理论基础壮大起来。
1698年,德国的Leibniz对中国传去的“八卦”产生了浓厚的兴趣,他预言:这将对科学研究非常重要,并提出了用机器代替人进行逻辑思维活动的设想,为此他还写了一封热情洋溢的信给当时的康熙皇帝,希望与中国学者共同研究八卦,进行文化交流。但当时的“天朝大国”闭关自守,对之自然是“不屑一顾”。
至1847年,英国的Boole-George发表了《逻辑学的数学分析》,紧接着于1854年他又发表《思维规律》,建立了逻辑代数(俗称Boole代数),但这一理论并没有引起人们的重视;直到1936年,美国麻省理工学院的Shannon将逻辑代数用于电子电路后,人们开始认识到:它是电路设计的理论根据和主要分析手段,紧接着于1946年,第一台电子计算机问世,二进制被用来作为计算机的基本数而引起人们的重视;又为解决它表示数太过冗长的致命弱点,开发出八进制、十六进制等等。这样,数冲破了十进制原有的包围,形成了应用数学的燎原之势。
总之,数的发展历程基本呈现:出现早、承认慢、系统理论互关联的特点。
附录 数的发展历程一览表
年代
对应中国年代
国家
主 要 成 就
旧石器晚期
伏羲时代
中国
八卦图出现,标志着数与二进制的诞生
-4200~-2200
黄帝族成契时代~唐尧起时期
中国
象形字诞生,有《洛书》《河图》数学文献
巴比伦
出现以石记数及六十进位制
埃及
象形字出现
-1850
夏槐王朝
埃及
纸草文书中有了分数记载
-1650
夏发王朝
埃及
Ahmes纸草文书中,将分数分子化为1进行计算
-600
周定王5年
巴比伦
泥版文书中以“□”代表零
-400左右
周安王2年
希腊
Hippasus提出了有无理数存在
-300
周赦王15年
希腊
Euclid《几何原本》用近似有理数取代无理数
-100
汉武帝天汉元年
中国
《周髀算经》记载了具体分数的计算
月1世纪
西汉
美国
印第安人马雅族用“□”表示零
100-200
东汉
中国
《九章算术》《孙子算经》含有了分数的运算法则及负数的概念
850
唐宣宗大中4年
印度
Mahavira写成《算术精要》,提出零的运算法则
920
梁末帝贞明5年,契丹太祖神册5年
叙利亚
Al-Battanl引入小数
1299
元成宗大德3年
中国
朱世杰《算学启蒙》有了负数的运算法则
1522
明世宗嘉靖元年
英国
Tonstall首用阿拉伯数字
1545
明世宗嘉靖24年
意大利
Cardana引入诡辩量(复数)
1572
明隆庆6年
意大利
Bcmbelli用复数得出一元三次方程的通解
1585
明万历13年
比利时
Stevin《论十进制》出版
1620
明泰昌元年
荷兰
Girard用“-”表示负数
1637
清崇德2年,明崇祯10年
法
Descartes命名虚数imaginary number
1689
清康熙28年
德
Leibniz指出八卦对科学研究很重要,提出了用机器代替人进行逻辑思维活动的设想
1747
清乾隆12年
法
D/Alem将有理数与虚数同样看待
1777
清乾隆42年
瑞士
Euler创立复数论
1801
清嘉庆6年
德
Guass系统将复数与几何建立关系
1847
清道光27年
英
Boole创立逻辑代数
1872
清同治11年
德
Dedekind命名有理数、无理数与实数
1874
清同治13年
德
Cantor证明实数与数轴上点一一对应
1891
清光绪17年
意大利
Peano提出正整数公理
1936
民国25年
美
Shannon将逻辑代数用于电子电路
1946
民国35年
美
第一台电子计算机问世
3.2复数的四则运算(1)――加减与乘法
[教学目标]
[教学重点]复数的加、减、乘运算
[教学难点]复数范围内分解因式
[教学过程]
二、新课内容:本节中a、b、c、d、x、y∈R
1、复数的加法与多项式加法类似:a+bi+(c+di)=(a+c)+(c+d)i两个复数的和仍然是一个复数
容易验证:复数的加法满足交换律和结合律,即:z1+z2=z2+z1,(z1+z2)+z3=z1+(z2+z3)
2、复数减法怎么办?实数当中,减法是加法的逆运算,即a+b=c,b称c与a的差,记作c-a
同理,对于复数,c+di+(x+yi)=a+bi,x+yi也称a+bi与c+di的差,记作(a+bi)-(c+di)
由加法定义,c+x=a,d+y=b,解得x=a-c,y=b-d,于是a+bi-(c+di)=(a-c)+(c-d)i两个复数的差仍然是一个复数
你能总结出复数加减运算的一般规律吗?
两个复数相加减,就是把他们的实部和虚部分别进行加减
练习:教材P108----1
3、复数的乘法: .
.
指出这一法则也是一种规定,由于它与多项式乘法运算法则一致,因此,不需要记忆这个公式.注意i2=-1
复数乘法也满足交换律、结合律以及分配律.
练习教材P108---2
思考:a>0时,方程x2+a=0在复数范围内的解是什么?(± i)
i)
例1、计算求 .
.
此例的解答可由学生自己完成.(a2+b2)
说明:将a-bi称a+bi的共轭复数,记作 =a-bi
=a-bi
思考1:一个复数z,什么情况下是实数?( =z)
=z)
思考2:在复数范围内,你能将x2+y2分解因式吗?(x2+y2=(x+yi((x-yi))
例2、在复数范围内分解因式x2+2x+5,
解:x2+2x+5=(x+1)2+4=(x+1+2i)(x+1-2i)
练习:教材P108---3,4,5
三、总结:a+bi±(c+di)=(a±c)+(c±d)i,两个复数相加减,就是把他们的实部和虚部分别进行加减
 ,
, =a-bi,一个复数z是实数
=a-bi,一个复数z是实数
 =z
=z
[作业]教材P111---1,2,5,6,10
[补充习题]
1、z1,z2分别为非零复数,A=z1 +z2
+z2 ,B=z1
,B=z1 +z2
+z2 ,问A、B能否比较大小,如果可以,比较它们的大小;不能说明理由
,问A、B能否比较大小,如果可以,比较它们的大小;不能说明理由
2、判断 和
和 什么关系
什么关系
[答案]
1、可以比较大小,A≤B
2、相等
备课资料:复数乘法的交换律、结合律及乘法对加法的分配律证明过程
复数的乘法满足交换律、结合律以及乘法对加法的分配律.证明如下。
设 ,
, ,
,
(1)∵ 


 ∴
∴

(2)∵ 













∴

(3)∵ 











 ∴
∴

3.2复数的四则运算(2)――乘方与除法
[教学目标]
[教学重点]复数的乘方、除法运算
[教学难点]复数综合运算
[教学过程]
二、新课内容:
一、在实数运算中,有了加而逆运算出现减,有了乘逆运算而出现除,叠运算出现乘方,复数乘方与除法怎么办呢?
1、复数乘方与实数乘方类似
z,z1,z2是复数,m、n为正整数,则zmzn=zm+n,(zm)n=zmn,(z1z2)n=z1nz2n
真正计算时,涉及了i的乘方,计算i1,i2,i3,i4,i5的值,由之你能得到什么结论?
结论:i4n=1,i4n+1=i,i4n+2=-1,i4n+3=-i
例1、设 ,求证:(1)
,求证:(1) ;(2)
;(2)
说明:(1)实数集中的乘法公式在复数集中仍然成立;(2)复数的混合运算也是乘方,乘除,最后加减,有括号应先处括号里面的.
变形1:如果 ,则
,则 与
与 还成立吗?(成立)
还成立吗?(成立)
变形2:能写出x3=1的三个根吗?(1, ,
, )
)
2、复数的除法:复数的除法也是乘法的逆运算,z1z=z2,称z为z2和z1的商 ,记作z= ,这样计算除法的总体思路是变成乘法计算
,这样计算除法的总体思路是变成乘法计算
例2、计算
解:[方法一]设 =x+yi,(x,y∈R),于是2-i=(3-4i)(x+yi)=3x+4+(3y-4x)i,,于是
=x+yi,(x,y∈R),于是2-i=(3-4i)(x+yi)=3x+4+(3y-4x)i,,于是
 ,解得
,解得 ,所以
,所以 =
= +
+ i
i
说明:根据除法是乘法的逆运算,常常将除法变成乘法,根据复数相等得到除法的值。
在学习无理数时,要花简一个分母含有根式的式子,我们常常进行分母有理化,如 =
=
 =2+
=2+ ,相应的复数是否分母也可以实数化呢?又如何进行实数化?
,相应的复数是否分母也可以实数化呢?又如何进行实数化?
[方法二]  =
= =
= =
= +
+ i
i
说明:复数除法的另一方法是分母实数化,实数化的具体技巧是分子、分母同乘分母的共轭复数
例3、求S= 的值
的值
解:S=1+2i+3i2+4i3+…………+100i99 ①
iS= i+2i2+3i3+…………+99i99+100i100 ②
①-②得:(1-i)S=1+i+i2+i3+……+i99-100= -100=-100,S=
-100=-100,S= =
= =-50(1+i)
=-50(1+i)
备用课堂练习:教材P110----练习题
三、小结:i4n=1,i4n+1=i,i4n+2=-1,i4n+3=-i
复数乘方与实数乘方类似
复数除法有两个思路,一根据除法是乘法的逆运算,常常将除法变成乘法,根据复数相等得到除法的值;二是分母实数化,实数化的具体技巧是分子、分母同乘分母的共轭复数
[补充习题]
四、作业:教材P111---3,4,7,8,9
1、求7-24i的平方根
2、求函数f(n)=( )n+(
)n+( )n,n∈N的值域
)n,n∈N的值域
[答案]
1、±(4-3i)
2、{2,0,-2}
3.3复数的几何意义
[教学目标]
[教学重点]复数减法法则.
[难点]对复数减法几何意义理解和应用.
教学过程设计
一、引入新课
实数与数轴上的点一一对应,复数a+bi取决于什么?能否用几何形式来体现?(板书课题:复数的几何意义)
二、新课内容
三、情感态度和价值观:体会知识的渐进功能
1、复数z=a+bi(a,b∈R)取决于点(a,b),而后者可以通过点的坐标来体现,这样建立直角坐标系来表示复数的平面称复平面,x轴称实轴,反应一个复数的实部,y轴称虚轴,除原点外表示复数的虚部。
这样:复数a+bi 复平面内的点(a,b)
复平面内的点(a,b)
思考:实数在复平面内的位置落在___________;唇虚数呢?___________
2、点Z(a,b)又与向量 对应,这样得到
对应,这样得到


这样,复数z=a+bi说成点Z或向量 ,相等的向量表示相同的复数
,相等的向量表示相同的复数
向量 的模叫做复数z=a+bi的模,记作|z|或|a+bi|=
的模叫做复数z=a+bi的模,记作|z|或|a+bi|=
思考:|z|,| |有什么关系?
|有什么关系?
练习:教材P130----练习1、2、3、4
例1、设z∈Z,满足下列条件的点Z的集合图形是是什么?
(1)|z|=2 (2)2<|z|<3 教材113页例3
3、复数加减法的有什么几何意义?
可以根据向量加减法的几何意义得到。设z= +
+ i(
i( ,
, ∈R),z1=
∈R),z1= +
+ i(
i( ,
, ∈R),对应向量分别为
∈R),对应向量分别为 ,
, 如图
如图
由于复数减法是加法的逆运算,设z=( -
- )+(
)+( -
- )i,所以z-z1=z2,z2+z1=z,由复数加法几何意义,以
)i,所以z-z1=z2,z2+z1=z,由复数加法几何意义,以
 为一条对角线,
为一条对角线,  1为一条边画平行四边形,那么这个平行四边形的另一边
1为一条边画平行四边形,那么这个平行四边形的另一边  2所表示的向量OZ2就与复数z-z1的差(
2所表示的向量OZ2就与复数z-z1的差( -
- )+(
)+( -
- )i对应,如图.
)i对应,如图.

在这个平行四边形中与z-z1差对应的向量是只有向量  2吗?
2吗?
还有
 . 因为OZ2
. 因为OZ2  Z1Z,所以向量
Z1Z,所以向量  ,也与z-z1差对应.向量
,也与z-z1差对应.向量  是以Z1为起点,Z为终点的向量.
是以Z1为起点,Z为终点的向量.
概括一下复数减法几何意义是:两个复数的差z-z1与连接这两个向量终点并指向被减数的向量对应.
(1)|z-1-i|=|z+2+i|;(2)|z+i|+|z-i|=4;(3)|z+2|-|z-2|=1.
思考:对于实数a,b有|ab|=|a||b|,对于向量则有| |≤|
|≤| ||
|| |,对于复数|z1z2|与|z1||z2|有什么关系,证明你的结论
|,对于复数|z1z2|与|z1||z2|有什么关系,证明你的结论
[补充习题]
四、布置作业P115-----习题3。3
1、复数z1,z2分别满足|z1|=1,|z2|=|z
2、(1+i)z1=-1+5i,z2=a-2-i,|z1- |<|z1|,求a的取值范围
|<|z1|,求a的取值范围
[答案]
1、≥ -1,
-1,
2、1<a<7
复数的复习
一、知识界面:
1、概念
⑴形如  的数,我们把它们叫做复数.其中a叫做这个复数的实部,b叫做虚部
的数,我们把它们叫做复数.其中a叫做这个复数的实部,b叫做虚部

⑵两个复数相等充要条件是它们的实部与虚部分别对应相等
⑶两个复数,只要含有实数就不能比较大小
2、复数的运算:
⑴a+bi±(c+di)=(a±c)+(c±d)i,两个复数相加减,就是把他们的实部和虚部分别进行加减
⑵ ,与多项式乘法类似
,与多项式乘法类似
⑶复数的乘方遵循实数的乘方法则,注意i2=-1
⑷复数的除法,一是设出按乘法及复数相等求出,二是进行分母实数化(分子、分母同成分母的共轭复数)
3、复数的几何意义:
复平面内的点Z(a,b) 复数z=a+bi(a,b∈R)
复数z=a+bi(a,b∈R) 向量
向量
⑴两个复数相加减,就是把他们的实部和虚部分别进行加减
⑵复数模的性质:|a+bi|= ,
,
 ,
, ,
, ;
; (
( );
); 。
。
⑶共轭复数的性质: =a-bi
=a-bi
z∈R z=
z= ;虚数z为纯虚数
;虚数z为纯虚数 z+
z+ =0;
=0; =
= ,
,  =
= ,
, =
= ,z
,z =|z|2,
=|z|2,
例1、z是虚数,ω=z+ ,求证:ω∈R的充要条件是|z|=1(教材P118---6)
,求证:ω∈R的充要条件是|z|=1(教材P118---6)
例2、z1,z2,z3∈C,|z1|=|z2|=1,|z1+z2|= ,求|z1-z2|(教材P1118---7)
,求|z1-z2|(教材P1118---7)
例3、在复数范围内解关于a,b,c的实系数一元二次方程ax2+bx+c=0
解:原方程可以化为a(x+ )2=
)2= -c, (x+
-c, (x+ )2=
)2= ,b2-4ac≥0时,x=
,b2-4ac≥0时,x= 根为实数;如果b2-4ac<0, x+
根为实数;如果b2-4ac<0, x+ =±
=± ,x=
,x= 跟为一对共轭虚数
跟为一对共轭虚数
练习1:在复数范围内解方程x3+8=0
练习2:在复数范围内分解因式:2x3+16
说明:对于系数为实数的方程,如果有虚数根,其共轭复数也是其一个根
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com