
山东省高密市第二学期数学期末考试
(满分120分,时间90分钟)
一、选择题(3×10=30分)
1. 下列写法不正确的是( ).
(A)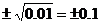 (B)
(B)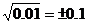
(C)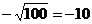 (D)
(D)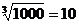
2.在下列各组根式中,是同类二次根式的是( ).
(A)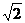 和
和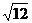 (B)
(B)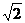 和
和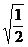
(C)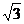 和
和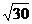 (D)
(D)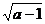 和
和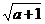
3.在下列函数中,当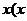 >
>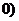 增大时,
增大时,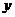 反而减小的函数是().
反而减小的函数是().
(A)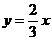 (B)
(B) 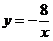 (C)
(C)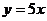 (D)
(D) 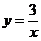
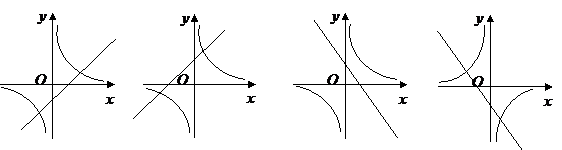 4.函数
4.函数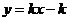 与
与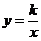 在同一坐标系中的图象大致是( ).
在同一坐标系中的图象大致是( ).
(A) (B) (C) (D)
5.若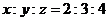 ,则下列各式中正确的是().
,则下列各式中正确的是().
(A)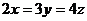 (B)
(B) 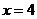
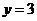
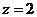
(C)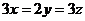 (D)
(D)
6.Rt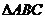 中,
中,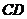 是斜边
是斜边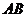 上的高,此图中共有
上的高,此图中共有 个和Rt
个和Rt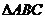 不同的三角形与
不同的三角形与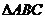 相似,则
相似,则 的值为( ).
的值为( ).
(A)1 (B) 2 (C) 3 (D) 4
7.当∠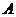 为锐角,且
为锐角,且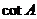 的值小于
的值小于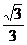 时,∠
时,∠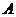 ( ).
( ).
(A)小于30° (B)大于30° (C) 小于60° (D) 大于60°
8.某人沿坡度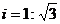 的桥向上走50米,这时,他离地面的高度是( ).
的桥向上走50米,这时,他离地面的高度是( ).
(A) 20米 (B) 24米
(C) 25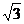 米 (D) 25米
米 (D) 25米
9.如图,在矩形 中,
中,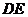
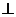
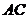 于
于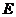 ,设
,设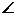
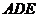 =
=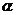 ,且cos
,且cos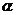 =
=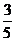
 ,
,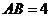 则
则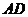 的长为( ) .
的长为( ) .
(A) 4.5
(B) 5 (C) 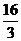 (D) 6
(D) 6
10. 样本101、98、102、100、99的标准差是( ).
(A) 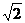 (B) 0
(C) 1
(D) 2
(B) 0
(C) 1
(D) 2
二 、 填空题 (3 10=30分)
10=30分)
11. 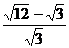
 =
.
=
.
12. 在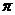 ,
,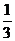 ,
, 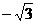 ,
,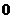 ,
,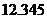 ,
,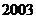 ,
,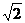 -1这些实数中,是无理数的为
.
-1这些实数中,是无理数的为
.
13. 若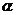 为整数,且点
为整数,且点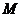
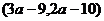 在第四象限,则
在第四象限,则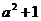 的值为
.
的值为
.
14.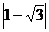
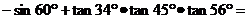 .
.
 15.
写出一个不经过第二象限的一次函数解析式
.
15.
写出一个不经过第二象限的一次函数解析式
.
16.如图,已知:
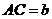 ,
,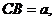
若△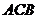 ∽△
∽△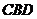 ,写出
,写出 与
与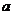 、
、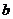 之间满足的关
之间满足的关
系式 .
17. 马路上有一电线杆在地面的影长为40米,同时高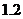 米的
米的
测杆在地面上的影长为2米,则电线杆的高为 .
18.一艘船向东航行,上午8时到达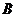 处,看到有一灯塔在它的北偏东
处,看到有一灯塔在它的北偏东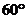 ,距离为72海里的
,距离为72海里的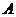 处,上午10时到达
处,上午10时到达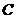 处,看到灯塔在它的正北方向,则这艘船航行的速度为
.
处,看到灯塔在它的正北方向,则这艘船航行的速度为
.
19.如果样本 的标准差是
的标准差是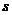 ,那么样本
,那么样本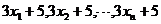 的方差是
.
的方差是
.
20. 从标有数字1~5的五张卡片中,随意抽出两张,将下列事件发生的机会按从小到大的顺序排成一列:抽出的两张卡片上的数字之和恰为(1)奇数;(2)素数;(3)偶数;(4)5的倍数;(5)小于3的数 .
三、 解答题(10 6=60分)
6=60分)
21.(10分)数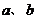 在数轴上的位置如图所示,化简:
在数轴上的位置如图所示,化简: +
+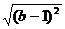 -
- .
.
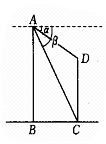 22.(10分)如图,两建筑物水平距离
22.(10分)如图,两建筑物水平距离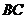 为24米,从点
为24米,从点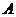 测得点
测得点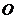 的俯角
的俯角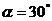 ,测得点
,测得点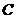 的俯角
的俯角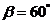 ,求
,求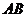 和
和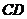 两座建筑物的高 (结果保留根号) .
两座建筑物的高 (结果保留根号) .
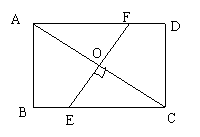
23.(10分)矩形纸片的长为8cm,宽为6cm,把纸片对折,使相对顶点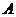 、
、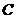 重合,求折痕
重合,求折痕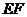 的长.
的长.
 |
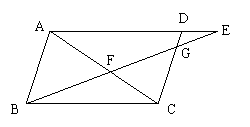 24.(10分)如图,在□
24.(10分)如图,在□ 中,过B做直线交
中,过B做直线交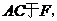 交
交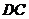 于
于 ,交
,交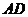 的延长线于
的延长线于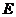 .试说明:
.试说明: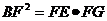 .
.
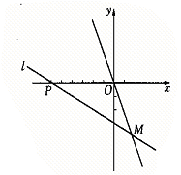 25.(10分)直线
25.(10分)直线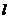 与
与 轴交于点
轴交于点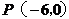 ,与直线
,与直线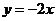 在
在 轴下方交于点
轴下方交于点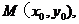 且
且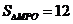 ,求直线
,求直线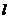 的解析式.
的解析式.
26.(10分)已知反比例函数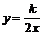 其中一次函数
其中一次函数 其中一次函数的图象经过
其中一次函数的图象经过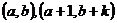 两点.
两点.
(1)求反比例函数的解析式;
(2)如图,已知点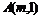 在第一象限,且同时在上述两个函数图像上,求点
在第一象限,且同时在上述两个函数图像上,求点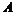 坐标;
坐标;
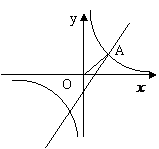 (3)
(3) 利用(2)的结果,请问:在
利用(2)的结果,请问:在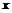 轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com