
2006年聊城市普通高中招生统一考试(实验区)
第Ⅰ卷
一、选择题(本题共12个小题,每小题4分.在每小题给出的四个选项中,只有一项符合题目
1.下列运算正确的是( )
A.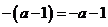 B.
B.
C.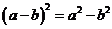 D.
D.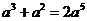
2.如图,由几个小正方体组成的立体图形的左视图是( )

3.下列事件中确定事件是( )
A.掷一枚均匀的硬币,正面朝上
B.买一注福利彩票一定会中奖
C.把4个球放入三个抽屉中,其中一个抽屉中至少有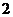 个球
个球
D.掷一枚六个面分别标有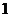 ,
,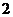 ,
,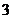 ,
,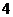 ,
, ,
,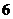 的均匀正方体骰子,骰子停止转动后奇数点朝上
的均匀正方体骰子,骰子停止转动后奇数点朝上
4.如图,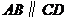 ,下列结论中正确的是( )
,下列结论中正确的是( )
A.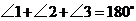 B.
B.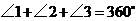
C.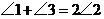 D.
D.
5.已知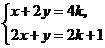 且
且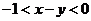 ,则
,则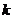 的取值范围为( )
的取值范围为( )
A.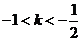 B.
B.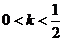 C.
C.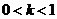 D.
D.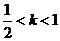
6.顺次连接矩形各边中点所得的四边形( )
A.是轴对称图形而不是中心对称图形 B.是中心对称图形而不是轴对称图形
C.既是轴对称图形又是中心对称图形 D.没有对称性
7.已知点 ,
,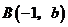 ,
,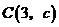 都在反比例函数
都在反比例函数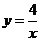 的图像上,则
的图像上,则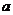 ,
,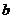 ,
,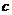 的大小关系为( )
的大小关系为( )
A.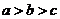 B.
B.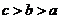 C.
C.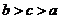 D.
D.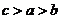
8.某款手机连续两次降价,售价由原来的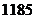 元降到
元降到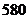 元.设平均每次降价的百分率为
元.设平均每次降价的百分率为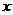 ,则下面列出的方程中正确的是( )
,则下面列出的方程中正确的是( )
A.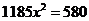 B.
B.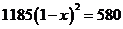
C.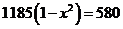 D.
D.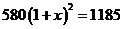
9.如图,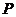 是
是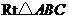 斜边
斜边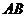 上任意一点(
上任意一点( ,
,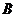 两点除外),过
两点除外),过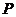 点作一直线,使截得的三角形与
点作一直线,使截得的三角形与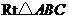 相似,这样的直线可以作( )
相似,这样的直线可以作( )
A.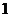 条 B.
条 B.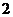 条 C.
条 C.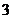 条 D.
条 D.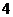 条
条
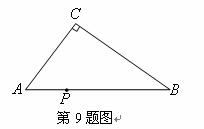
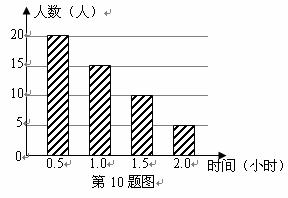
A.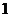 小时 B.
小时 B.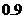 小时
小时
C.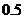 小时 D.
小时 D.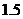 小时
小时
11.如图, 是
是 的内切圆,
的内切圆,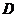 ,
, ,
,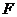 为三个切点,若
为三个切点,若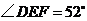 ,则
,则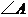 的度数为( )
的度数为( )
A.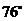 B.
B.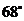 C.
C. D.
D.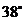

12.小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
输入
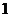
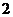
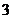
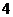

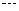
输出
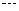
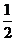

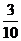
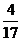
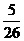
当输入数据是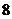 时,输出的数是( )
时,输出的数是( )
A.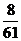 B.
B. C.
C. D.
D.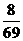
第Ⅱ卷
二、填空题(本题共5个小题,每小题4分,共20分.只要求填写最后结果)
13.化简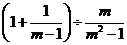 的结果是_______________.
的结果是_______________.
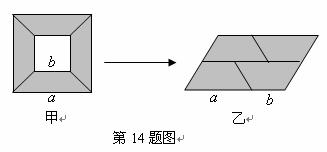
14.从边长为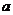 的大正方形纸板中挖去一个边长为
的大正方形纸板中挖去一个边长为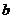 的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算阴影部分的面积可以验证公式______________.
的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算阴影部分的面积可以验证公式______________.
15.把一组数据中的每一个数据都减去 ,得一组新数据,若求得新一组数据的平均数是
,得一组新数据,若求得新一组数据的平均数是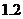 ,方差是
,方差是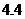 ,则原来一组数据的平均数和方差分别为_______________.
,则原来一组数据的平均数和方差分别为_______________.
16.在平面直角坐标系中,已知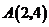 ,
,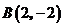 ,
, ,则过
,则过 ,
,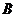 ,
, 三点的圆的圆心坐标为_______________.
三点的圆的圆心坐标为_______________.
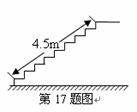
17.实验中学要修建一座图书楼,为改善安全性能,把楼梯的倾斜角由原来设计的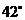 改为
改为 .已知原来设计的楼梯长为
.已知原来设计的楼梯长为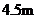 ,在楼梯高度不变的情况下,调整后的楼梯多占地面_____________
,在楼梯高度不变的情况下,调整后的楼梯多占地面_____________ .(精确到
.(精确到 )
)
三、解答题(本题共8个小题,共82分.解答应写出文字说明、证明过程或推演步骤)
18.(本题满分8分)用配方法解方程: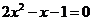 .
.
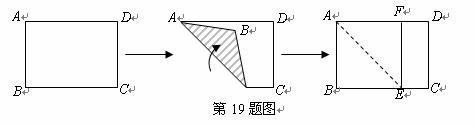
19.(本题满分8分)如图,将一张矩形纸片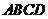 折叠,使
折叠,使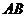 落在
落在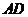 边上,然后打开,折痕为
边上,然后打开,折痕为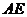 ,顶点
,顶点 的落点为
的落点为 .你认为四边形
.你认为四边形 是什么特殊四边形?请说出你的理由.
是什么特殊四边形?请说出你的理由.
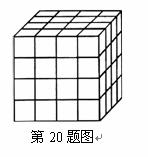
20.(本题满分10分)如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成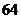 个大小相同的小正方体.从这些小正方体中任意取出一个,求取出的小正方体:
个大小相同的小正方体.从这些小正方体中任意取出一个,求取出的小正方体:
(1)三面涂有颜色的概率;
(2)两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
21.(本题满分10分)如图,在由边长为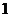 的小正方形组成的方格纸中,有两个全等的三角形,即
的小正方形组成的方格纸中,有两个全等的三角形,即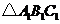 和
和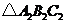 .
.
(1)请你指出在方格纸内如何运用平移、旋转变换,将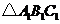 重合到
重合到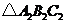 上;
上;
(2)在方格纸中将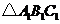 经过怎样的变换后可以与
经过怎样的变换后可以与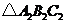 成中心对称图形?画出变换后的三角形并标出对称中心.
成中心对称图形?画出变换后的三角形并标出对称中心.
22.(本题满分10分)为体现党和政府对农民健康的关心,解决农民看病难问题,我市某县于今年 月
月 日开始全面实行新型农村合作医疗,对住院农民的医疗费实行分段报销制.下面是该县县级医疗机构住院病人累计分段报销表:
日开始全面实行新型农村合作医疗,对住院农民的医疗费实行分段报销制.下面是该县县级医疗机构住院病人累计分段报销表:
医疗费
报销比例(%)
500元以下(含500元)
20
500元(不含)至2000元部分
30
2000元(不含)至5000元部分
35
5000元(不含)至10000元部分
40
10000元以上部分
45
(例:某住院病人花去医疗费 元,报销金额为
元,报销金额为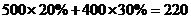 (元))
(元))
(1)农民刘老汉在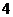 月份因脑中风住院花去医疗费
月份因脑中风住院花去医疗费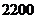 元,他可以报销多少元?
元,他可以报销多少元?
(2)写出医疗费超过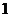 万元时报销数额
万元时报销数额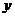 (元)与医疗费
(元)与医疗费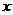 (元)之间的函数关系式;
(元)之间的函数关系式;
(3)刘老汉在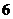 月份因脑中风复发再次住院,这次报销医疗费
月份因脑中风复发再次住院,这次报销医疗费 元,刘老汉这次住院花去医疗费多少元?
元,刘老汉这次住院花去医疗费多少元?
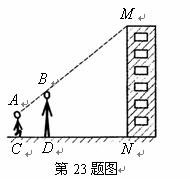
23.(本题满分10分)亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部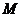 ,颖颖的头顶
,颖颖的头顶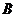 及亮亮的眼睛
及亮亮的眼睛 恰在一条直线上时,两人分别标定自己的位置
恰在一条直线上时,两人分别标定自己的位置 ,
,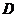 .然后测出两人之间的距离
.然后测出两人之间的距离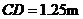 ,颖颖与楼之间的距离
,颖颖与楼之间的距离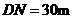 (
( ,
,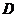 ,
,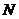 在一条直线上),颖颖的身高
在一条直线上),颖颖的身高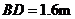 ,亮亮蹲地观测时眼睛到地面的距离
,亮亮蹲地观测时眼睛到地面的距离 .
.
你能根据以上测量数据帮助他们求出住宅楼的高度吗?
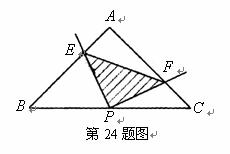
24.(本题满分12分)如图,在等腰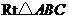 中,
中,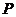 是斜边
是斜边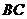 的中点,以
的中点,以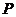 为顶点的直角的两边分别与边
为顶点的直角的两边分别与边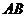 ,
,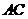 交于点
交于点 ,
,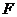 ,连接
,连接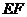 .当
.当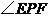 绕顶点
绕顶点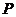 旋转时(点
旋转时(点 不与
不与 ,
,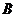 重合),
重合),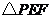 也始终是等腰直角三角形,请你说明理由.
也始终是等腰直角三角形,请你说明理由.
25.(本题满分14分)一家用电器开发公司研制出一种新型电子产品,每件的生产成本为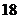 元,按定价
元,按定价 元出售,每月可销售
元出售,每月可销售 万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价
万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价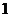 元,月销售量可增加
元,月销售量可增加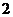 万件.
万件.
(1)求出月销售量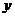 (万件)与销售单价
(万件)与销售单价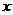 (元)之间的函数关系式(不必写
(元)之间的函数关系式(不必写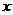 的取值范围);
的取值范围);
(2)求出月销售利润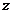 (万元)(利润=售价-成本价)与销售单价
(万元)(利润=售价-成本价)与销售单价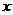 (元)之间的函数关系式(不必写
(元)之间的函数关系式(不必写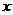 的取值范围);
的取值范围);
(3)请你通过(2)中的函数关系式及其大致图像帮助公司确定产品的销售单价范围,使月销售利润不低于 万元.
万元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com