
2007年北京市高级中等学校招生统一考试(课标卷)
数 学 试 卷
(本试卷满分120分.考试时间120分钟)
第Ⅰ卷 (共32分)
一、选择题(共8个小题,每小题4分,共32分)
1. 的倒数是( )
的倒数是( )
A.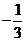 B.
B.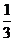 C.
C. D.
D.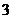
2.国家游泳中心-“水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260 000平方米,将260 000用科学记数法表示应为( )
A.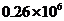 B.
B.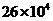 C.
C.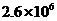 D.
D.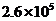
 3.如图,
3.如图,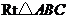 中,
中, ,
,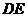 过点
过点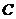 且平行于
且平行于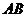 ,若
,若 ,则
,则 的度数为( )
的度数为( )
A.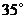 B.
B.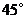 C.
C. D.
D.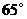
4.若 ,则
,则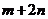 的值为( )
的值为( )
A.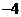 B.
B.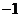 C.0 D.4
C.0 D.4
5.北京市2007年5月份某一周的日最高气温(单位:℃)分别为25,28,30,29,31,32,28,这周的日最高气温的平均值为( )
A.
6.把代数式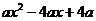 分解因式,下列结果中正确的是(
)
分解因式,下列结果中正确的是(
)
A.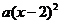 B.
B.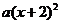 C.
C.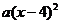 D.
D.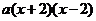
7.一个袋子中装有6个黑球3个白球,这些球除颜色外,形状、大小、质地等完全相同,在看不到球的条件下,随机地从这个袋子中摸出一个球,摸到白球的概率为( )
A. B.
B.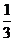 C.
C.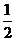 D.
D.
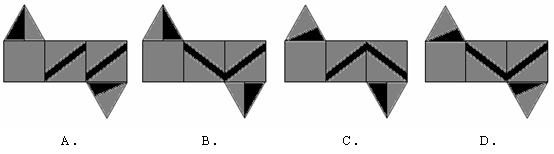
 8.右图所示是一个三棱柱纸盒,在下面四个图中,只有一个是这个纸盒的展开图,那么这个展开图是( )
8.右图所示是一个三棱柱纸盒,在下面四个图中,只有一个是这个纸盒的展开图,那么这个展开图是( )
第Ⅱ卷 (共88分)
二、填空题(共4个小题,每小题4分,共16分)
9.若分式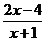 的值为0,则
的值为0,则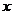 的值为
.
的值为
.
10.若关于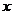 的一元二次方程
的一元二次方程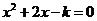 没有实数根,则
没有实数根,则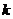 的取值范围是
.
的取值范围是
.
11.在五环图案内,分别填写五个数a,b,c,d,e,如图,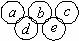 ,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如
,其中a,b,c是三个连续偶数(a<b),d,e是两个连续奇数(d<e),且满足a+b+c=d+e,例如 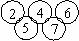 。请你在0到20之间选择另一组符号条件的数填入下图:
。请你在0到20之间选择另一组符号条件的数填入下图: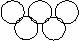 。
。
 12.右图是对称中心为点
12.右图是对称中心为点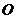 的正六边形.如果用一个含
的正六边形.如果用一个含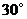 角的直角三角板的角,借助点
角的直角三角板的角,借助点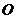 (使角的顶点落在点
(使角的顶点落在点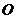 处),把这个正六边形的面积
处),把这个正六边形的面积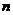 等分,那么
等分,那么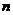 的所有可能的值是
.
的所有可能的值是
.
三、解答题(共5个小题,共25分)
13.(本小题满分5分)
计算: .
.
14.(本小题满分5分)
解方程: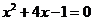 .
.
15.(本小题满分5分)
计算: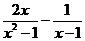 .
.
16.(本小题满分5分)
已知:如图, 是
是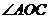 和
和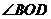 的平分线,
的平分线,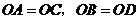 .
.
 求证:
求证: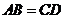 .
.
17.(本小题满分5分)
已知 ,求代数式
,求代数式 的值.
的值.
四、解答题(共2个小题,共10分)
 18.(本小题满分5分)
18.(本小题满分5分)
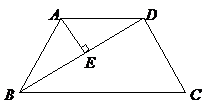
如图,在梯形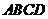 中,
中,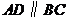 ,
,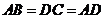 ,
, ,
,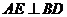 于点
于点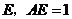 ,求梯形
,求梯形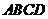 的高.
的高.
19.(本小题满分5分)
已知:如图, 是⊙O上一点,半径
是⊙O上一点,半径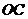 的延长线与过点
的延长线与过点 的直线交于
的直线交于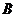 点,
点,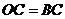 ,
,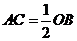 .
.
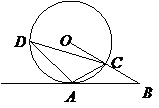 (1)求证:
(1)求证: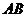 是⊙O的切线;
是⊙O的切线;
(2)若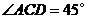 ,
,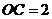 ,求弦
,求弦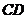 的长.
的长.
五、解答题(本题满分6分)
20.根据北京市水务局公布的2004年、2005年北京市水资源和用水情况的相关数据,绘制如下统计图表:
2005年北京市水资源分布图(单位:亿 )
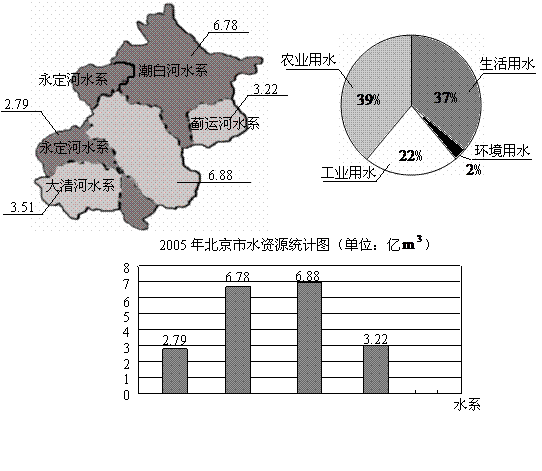
2004年北京市用水量统计图
)
2004年北京市用水量统计图



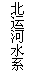
2005年北京市用水情况统计表
生活用水
环境用水
工业用水
农业用水
用水量
(单位:亿 )
)
13.38
6.80
13.22
占全年总用水量的比例

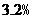
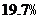
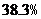
(1)北京市水资源全部由永定河水系、潮白河水系、北运河水系、蓟运河水系、大清河水系提供.请你根据以上信息补全2005年北京市水资源统计图,并计算2005年全市的水资源总量(单位:亿 );
);
(2)在2005年北京市用水情况统计表中,若工业用水量比环境用水量的6倍多0.2亿 ,请你先计算环境用水量(单位:亿
,请你先计算环境用水量(单位:亿 ),再计算2005年北京市用水总量(单位:亿
),再计算2005年北京市用水总量(单位:亿 );
);
(3)根据以上数据,请你计算2005年北京市的缺水量(单位:亿 );
);
(4)结合2004年及2005年北京市的用水情况,谈谈你的看法.
六、解答题(共2个小题,共9分)
21.(本小题满分5分)
在平面直角坐标系 中,
中,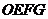 为正方形,点
为正方形,点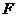 的坐标为
的坐标为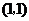 .将一个最短边长大于
.将一个最短边长大于 的直角三角形纸片的直角顶点放在对角线
的直角三角形纸片的直角顶点放在对角线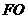 上.
上.
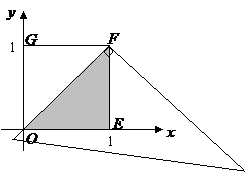
(1)如图,当三角形纸片的直角顶点与点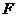 重合,一条直角边落在直线
重合,一条直角边落在直线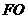 上时,这个三角形纸片与正方形
上时,这个三角形纸片与正方形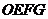 重叠部分(即阴影部分)的面积为
;
重叠部分(即阴影部分)的面积为
;
(2)若三角形纸片的直角顶点不与点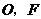 重合,且两条直角边与正方形相邻两边相交,当这个三角形纸片与正方形
重合,且两条直角边与正方形相邻两边相交,当这个三角形纸片与正方形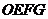 重叠部分的面积是正方形面积的一半时,试确定三角形纸片直角顶点的坐标(不要求写出求解过程),并画出此时的图形.
重叠部分的面积是正方形面积的一半时,试确定三角形纸片直角顶点的坐标(不要求写出求解过程),并画出此时的图形.
 |
22.(本小题满分4分)
在平面直角坐标系 中,反比例函数
中,反比例函数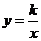 的图象与
的图象与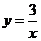 的图象关于
的图象关于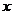 轴对称,又与直线
轴对称,又与直线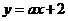 交于点
交于点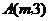 ,试确定
,试确定 的值.
的值.
七、解答题(本题满分7分)
23.如图,已知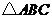 .
.
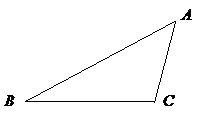 (1)请你在
(1)请你在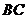 边上分别取两点
边上分别取两点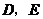 (
(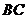 的中点除外),连结
的中点除外),连结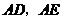 ,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
(2)请你根据使(1)成立的相应条件,证明 .
.
八、解答题(本题满分7分)
24.在平面直角坐标系 中,抛物线
中,抛物线 经过
经过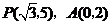 两点.
两点.
(1)求此抛物线的解析式;
(2)设抛物线的顶点为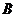 ,将直线
,将直线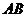 沿
沿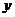 轴向下平移两个单位得到直线
轴向下平移两个单位得到直线 ,直线
,直线 与抛物线的对称轴交于
与抛物线的对称轴交于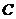 点,求直线
点,求直线 的解析式;
的解析式;
(3)在(2)的条件下,求到直线 距离相等的点的坐标.
距离相等的点的坐标.
 |
九、解答题(本题满分8分)
25.我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
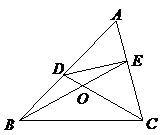 (1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
(1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
(2)如图,在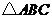 中,点
中,点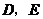 分别在
分别在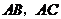 上,
上,
设 相交于点
相交于点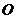 ,若
,若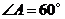 ,
,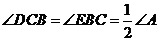 .
.
请你写出图中一个与 相等的角,并猜想图中哪个四边形
相等的角,并猜想图中哪个四边形
是等对边四边形;
(3)在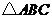 中,如果
中,如果 是不等于
是不等于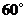 的锐角,点
的锐角,点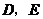 分别在
分别在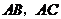 上,且
上,且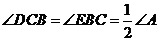 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com