
2006-2007学年度聊城市莘县第二学期期中检测
八年级数学试卷
(时间:100分钟 满分l20分)
一、选择题(本题共l0个小题.每小题3分.将唯一选项填在答卷相应位置)
1.下列说法①分式的分子分母都乘以a+2,分式的值不变;②分式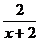 的值能等于0;③
的值能等于0;③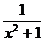 的值永远大于0;④方程
的值永远大于0;④方程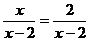 的解为x=2,其中正确的是
的解为x=2,其中正确的是
A.1个 B.2个 C.3个 D.4个
2.已知点P(2m+1,-2)存第四象限,那么m的取值范围
A.m>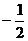 B.m<
B.m<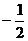 C.m≥
C.m≥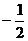 D.m≤
D.m≤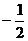
3.人体中成熟的细胞的平均直径为0.0000077米,用科学记数法表示为
A.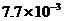 米 B.
米 B. 米 C.
米 C.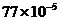 米 D.
米 D.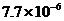 米
米
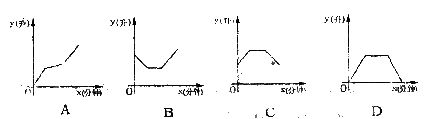
4.打开洗衣机在洗涤衣服时(洗衣机内原来无水)洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水洗衣中的水量y<升)与时间x(分钟)满足的函数关系式是
5.若一次函数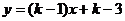 的图象不经过第二象限,则k的取值范围是
的图象不经过第二象限,则k的取值范围是
A.1<k<3 B.1<k≤3 C.1≤k≤3 D.k≠1
6.如图AB=AC,AD=AE,要使△ABD≌△ACE,须补充的条件是
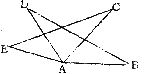
A.∠B=∠C B.∠D=∠E
C,∠BAC=∠EAD D.∠CAD=∠EAD
7.若函数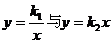 的图象交于(-2,5),则它们另一个交点为
的图象交于(-2,5),则它们另一个交点为
A,(2,-5) B.(5,-2) C.(-2,-5) D.(2,5)
8.已知反比例函数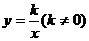 的图象在每一象限内y随x的增大而减小,则
的图象在每一象限内y随x的增大而减小,则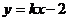 的大致图象是
的大致图象是
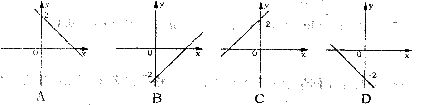
9.分式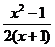 等于0,则x的值是
等于0,则x的值是
A.1
B.±1
C.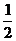 D.
D.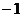
10.如图BD⊥AD,BC⊥AC,且AD=AC,则图中全等的三角形的对数是

A.0 B.1 C.2 D.3
二、填空题(共8个小题,每题3分)
11.计算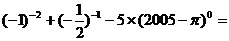 ____________.
____________.
12.张磊的教室在二楼,他上楼速度为x米/分,下楼速度为y米/分,则张磊上楼和下楼的平均速度为___________________.
13.直线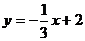 过点(____,0)(0,____) 14.如图由边长相等的黑白两色正方形按一定规律拼接而成,依次规律,设第x个图案中的白色正方形的个数为y,则y与x的关系式________________.
过点(____,0)(0,____) 14.如图由边长相等的黑白两色正方形按一定规律拼接而成,依次规律,设第x个图案中的白色正方形的个数为y,则y与x的关系式________________.
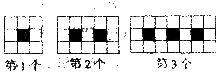
15.等腰三角形的周长10cm,则底边长y(cm)与腰长x(cm)的函数关系式为_______.x的取值范围为_______________.
16.直线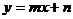 如图所示,化简
如图所示,化简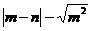 =________.
=________.
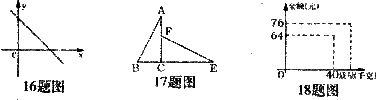
17.如图若△ABC≌△EFC,且CF=3cm,∠EFC=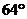 ,则BC=_____cm.∠B=_____
,则BC=_____cm.∠B=_____
18.周日小李同学用每千克0.8元的价格购进若干千克黄瓜去销售,在销售部分黄瓜之后,余下的每千克降价0.4元。全部售完销售金额与卖瓜的千克数之间的关系如图.则小李赚了___________元.
三、认真解答一定细心(共66分)
19.(7分)化简求值:
 .
.
20.(7分)在求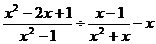 的值时,其中x=2007,但是甲同学抄错了,把2007抄成x=2070,但他的计算结果仍然是正确的,你能说明其中的原因吗?
的值时,其中x=2007,但是甲同学抄错了,把2007抄成x=2070,但他的计算结果仍然是正确的,你能说明其中的原因吗?
21.(7分)解方程:
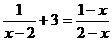
22.(7分)如图我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形边长均为l)根据象棋中“马”走“日”的规定.若“马”的位置在图中的点P.
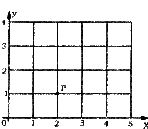
(1)写出下一步“马”可能到达的点的坐标.
(2)顺次连接(1)中的所有点得到的图形是什么图形.
(3)写出(1)中关于点P成中心对称的点.
23.(8分)已知直线y=2x+1和y=3x+b的交点在第三象限,写出常数b可能的两个数值.
24.(8分)为了鼓励市民节约用水,自来水公司制定了新的用水收费标准.每月用水量x(吨)与应付水费y(元)的函数关系式如图.
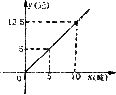
(1)求出月用水量不超过5吨时,Y与x之间的函数关系式.
(2)某居民某月用水量8吨应付的水费是多少?
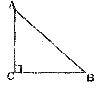
25.(10分)已知Rt△ABC中,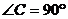 .
.
(1)根据要求作图(尺规作图,保留作图痕迹,不写画法)
①作∠BAC的平分线AD交BC于点D.
②作线段AD的垂直平分线交AB于点E,交AC于点F,垂足为点H.
③连结DF.
(2)在(1)的基础上写出一对全等三角形并加以证明。
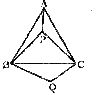
26.(12分)如图P是等边三角形ABC内的一点,连结PA、PB、PC.以BP为边作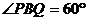 。且BQ=BP.连结CQ.
。且BQ=BP.连结CQ.
(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论.
(2)若PA:PB:PC=3:4:5,连结PQ,试判断△PQC:的形状.并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com