
2006-2007学年度德州市第二学期期中质量检测
八年级数学试卷
一、精心选一选,慧眼识金。(每小题3分,共24分,各小题的四个选项中,有且只有一个是符合题意的,把你认为符合题意的答案选出来,选错或不选或答案超过一个,均记零分)
1、在式子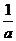 ,
,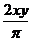 ,
, ,
,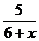 ,
,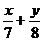 ,
,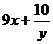 中,分式的个数是 ( )。
中,分式的个数是 ( )。
A、2 B、
2、若分式 的值等于零,那么
的值等于零,那么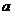 的取值范围是 ( )。
的取值范围是 ( )。
A、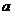 可取任意实数 B、
可取任意实数 B、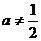
C、 D、
D、
3、下列变形不正确的是 ( )。
A、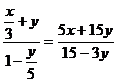 B、
B、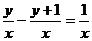
C、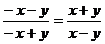 D、
D、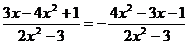
4、函数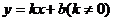 与
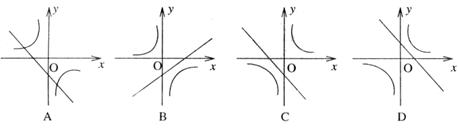
与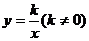 在同一坐标系中的图像可能是 ( )。
在同一坐标系中的图像可能是 ( )。
5、如图,一束光线从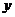 轴上点A(0,2)出发,经过
轴上点A(0,2)出发,经过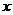 轴上点C反射后经过B(6,6)。则光线从A点到B点所经过的路程是(
)。
轴上点C反射后经过B(6,6)。则光线从A点到B点所经过的路程是(
)。
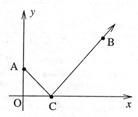
A、l0 B、
6、在反比例函数 的图像上有三点(
的图像上有三点( ,
,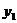 ),(
),(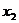 ,
,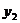 ),(
),(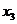 ,
, )且
)且 则下列各式正确的是 ( )。
则下列各式正确的是 ( )。
A、 B、
B、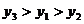
C、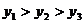 D、
D、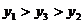
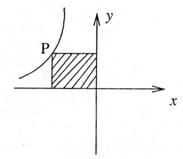
7、如图,点P是反比例函数图像上一点,过点P向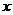 轴、
轴、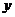 轴引垂线,得图中阴影部分的面积为4,则反比例函数解析式为 (
)。
轴引垂线,得图中阴影部分的面积为4,则反比例函数解析式为 (
)。
A、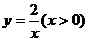 B、
B、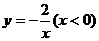
C、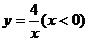 D、
D、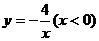
8、某化肥厂原计划每天生产化肥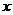 吨,由于采用了新技术,每天多生产化肥2吨,若完成l50吨的生产任务,现在可比原来节省5天,那么适合
吨,由于采用了新技术,每天多生产化肥2吨,若完成l50吨的生产任务,现在可比原来节省5天,那么适合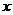 的方程为 ( )。
的方程为 ( )。
A、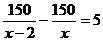 B、
B、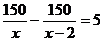
C、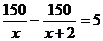 D、
D、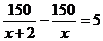
二、细心填一填,一锤定音。(本大题共8小题,每小题3分,共计24分)
9、某种感冒病毒的直径是0.00000012米,用科学记数法表示为____________米。
10、若△ABC中,AB=13,AC=15,高AD=12,则BC的长是____________。
11、试写出一个反比例函数的解析式____________,在同一坐标系中,使其图像与直线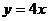 无交点。
无交点。
12、小丽根据下表,作了三个推测:
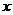
1
10
100
1000
10000
…

3
2.1
2.0l
2.00l
2.0001
…
(D 
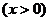 的值随
的值随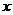 的增大越来越小;
的增大越来越小;
②
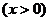 的值有可能等于2;
的值有可能等于2;
③
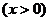 的值随
的值随 的增大越来越接近于2,则其中推测正确的有_________个。
的增大越来越接近于2,则其中推测正确的有_________个。
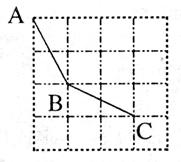
13、如图,是由边长为1m的正方形地砖铺设的地面示意图,小明沿图中所示的折线从A→B→C所走的路程为__________m。(结果保留根号)
14、某种蓄电池的电压为定值,使用此电源时,电流I(A)与可变电阻R(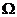 )之间的函数关系如图所示。当用电器的电流为l0A时,用电器的可变电阻为____________
)之间的函数关系如图所示。当用电器的电流为l0A时,用电器的可变电阻为____________ 。
。

15、规定 ,如
,如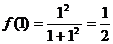 ;
; ;则:
;则: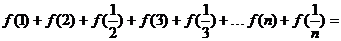 ____________。
____________。
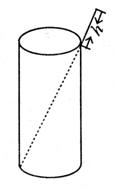
16、如图,将一根长20cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为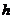 cm,则
cm,则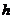 的取值范围是____________。
的取值范围是____________。
三、用心解一解,马到成功。(本大题共8小题,共计72分)
17、(本题满分8分)
①先化简代数式: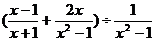 ,然后选取一个使原式有意义的
,然后选取一个使原式有意义的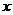 的值代入求值。
的值代入求值。
②解方程: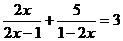
18、(本题满分6分)
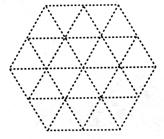
请在由边长为1的小正三角形组成的虚线网格中,画出1个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形。
19、(本题满分8分)
如图,一次函数 的图像与反比例函数
的图像与反比例函数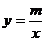 的图像交于A(-2,1)、B(1,
的图像交于A(-2,1)、B(1, )两点。
)两点。

(1) 求反比例函数和一次函数的解析式;
(2) 根据图像写出使一次函数的值大于反比例函数的值的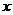 的取值范围。
的取值范围。
20、(本题满分8分)
有一旗杆不知其长,但有一旗绳从顶端垂下(绳长大于旗杆长)现有皮尺一只,试设计一方案测出旗杆的高度。(要求写出步骤及算式)
21、(本题满分8分)
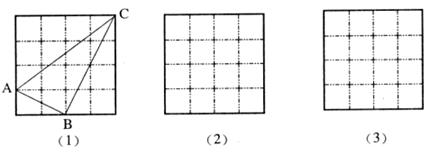
正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在图(1)的正方形网格中作出Rt△ABC。请你按照同样的要求,在图(2)(3)的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。
22、(本题满分l0分)
在新农村建设中,我市某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程队先单独做10天,那么剩下的工程还需要两队合做20天才能完成。
(1) 求乙工程队单独完成这项工程所需的天数。
(2) 求两队合做完成这项工程所需的天数。
23、(本题满分l2分)
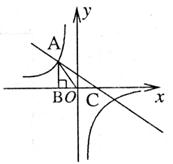
如图已知反比例函数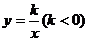 的图像经过点A(
的图像经过点A(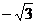 ,
,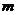 ),过点A作AB⊥
),过点A作AB⊥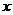 轴于B,且△AOB的面积为
轴于B,且△AOB的面积为 。
。
(1) 求 和
和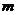 的值;
的值;
(2) 若一次函数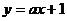 的图像经过点A,并且与
的图像经过点A,并且与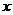 轴相交于点C,求点C的坐标。
轴相交于点C,求点C的坐标。
24、(本题满分l2分)
清朝康熙皇帝是我国历史上一位对数学很感兴趣的帝王。近日,西安发现了他的数学专著,其中有一文《积求勾股法》,他对“三边长为3,4,5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:
“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数。”
用现在的数学语言表述是:“若直角三角形的三边长分别为3,4,5的整数倍,设其面积为S,则第一步: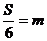 ;第二步:
;第二步: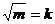 ;第三步:分别用3、4、5乘以
;第三步:分别用3、4、5乘以 ,得三边长。”
,得三边长。”
(1) 当面积S等于l50时,请用康熙的“积求勾股法”求出这个直角三角形的边长;
(2) 你能证明“积求勾股法”的正确性吗?请写出证明过程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com