
2007年哈尔滨市初中升学考试
数学试卷
第I卷 选择题(共30分)
一、选择题(每小题3分,共计30分)
1.一天早晨的气温是 ℃,中午的气温比早晨上升了
℃,中午的气温比早晨上升了 ℃,中午的气温是( )
℃,中午的气温是( )
A. ℃ B.
℃ B. ℃ C.
℃ C. ℃ D.
℃ D. ℃
℃
2.下列计算中,正确的是( )
A. B.
B.
C. D.
D.
3.下列图形中,既是中心对称图形又是轴对称图形的是( )

4.计算: 的结果是( )
的结果是( )
A. 5 B.6 C.7 D.8
5.随机掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,则这个骰子向上的一面点数是奇数的概率为( )
A. B.
B. C.
C. D.
D.
6.如图是某一立体图形的三视图,则这个立体图形是( )

A.正三棱柱 B.三棱锥 C.圆柱 D.圆锥
7.哈尔滨市为迎接第24届世界大学生冬季运动会,正在进行城区人行道路翻新,准备选用同一种正多边形地砖铺设地面.下列正多边形的地砖中,不能进行平面镶嵌的是( )

8.2007年我国铁路进行了第六次大提速,一列火车由甲市匀速驶往相距600千米的乙市,火车的速度是200千米/小时,火车离乙市的距离 (单位:千米)随行驶时间
(单位:千米)随行驶时间 (单位:小时)变化的函数关系用图象表示正确的是( )
(单位:小时)变化的函数关系用图象表示正确的是( )

9.如图,矩形纸片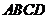 中,
中, ,把矩形纸片沿直线
,把矩形纸片沿直线 折叠,点
折叠,点 落在点
落在点 处,
处, 交
交 于点
于点 ,若
,若 ,则
,则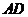 的长为( )
的长为( )

A. B.
B. C.
C. D.
D.
10.下列说法中,正确的说法有( )
①对角线互相平分且相等的四边形是菱形;
②一元二次方程 的根是
的根是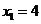 ,
,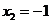 ;
;
③依次连接任意一个四边形各边中点所得的四边形是平行四边形;
④一元一次不等式 的正整数解有3个;
的正整数解有3个;
⑤在数据1,3,3,0,2中,众数是3,中位数是3.
A.1个 B.2个 C.3个 D.4个
第II卷 非选择题(共90分)
二、填空题(每小题3分,共计30分)
11.我国淡水面积大约为66 000千米 ,用科学记数法表示为 千米
,用科学记数法表示为 千米 .
.
12.分解因式: .
.
13.函数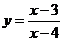 的自变量
的自变量 的取值范围是 .
的取值范围是 .
14.已知反比例函数 的图象经过点
的图象经过点 ,
,
则这个反比例函数的解析式是 .
15.如图, 是
是 的切线,
的切线, 为切点,
为切点, 交
交 于点
于点 ,
,
 ,
, ,则
,则 的值是 .
的值是 .

16.柜台上放着一堆罐头,它们摆放的形状见图:

第一层有 听罐头,
听罐头,
第二层有 听罐头,
听罐头,
第三层有 听罐头,
听罐头,
……
根据这堆罐头排列的规律,第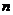 (
(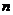 为正整数)层
为正整数)层
有
听罐头(用含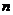 的式子表示).
的式子表示).
17.(此题只要求南岗区、道里区、道外区、香坊区、平房区的考生答)有4支球队要进行篮球比赛,赛制为单循环形式(每两队之间都赛一场),则一共需比赛 场.
*17.(此题只要求呼兰区、阿城区、松北区、双城市、五常市、尚志市、方正县、延寿县、巴彦县、木兰县、通河县、宾县、依兰县的考生答)直线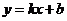 经过点
经过点 和
和 轴正半轴上的一点
轴正半轴上的一点 ,如果
,如果 (
(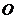 为坐标原点)的面积为2,则
为坐标原点)的面积为2,则 的值为 .
的值为 .
18.圆锥的底面直径是8,母线长是12,则这个圆锥侧面展开图的扇形圆心角是 度.
19.如图,用一段长为 ,设
,设 边长为
边长为 米,则菜园的面积
米,则菜园的面积 (单位:米
(单位:米 )与
)与 (单位:米)的函数关系式为
(单位:米)的函数关系式为
(不要求写出自变量 的取值范围).
的取值范围).

20.在 中,
中, ,
, ,
, ,点
,点 在直线
在直线 上,点
上,点 到直线
到直线 的距离为1,则
的距离为1,则 的长为 .
的长为 .
三、解答题(其中21~24题各6分,25~26题各8分,27~28题各10分,共60分)
21.(本题6分)
先化简,再求代数式 的值,其中
的值,其中 ,
, .
.
22.(本题6分)
 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.
(1)作出与 关于
关于 轴对称的
轴对称的 ;
;
(2)将 向下平移3个单位长度,画出平移后的
向下平移3个单位长度,画出平移后的 .
.

23.(本题6分)
如图, 是
是 的弦,矩形
的弦,矩形 的边
的边 与
与 交于点
交于点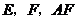 和
和 相交于点
相交于点 ,连接
,连接 .
.

(1)写出图中每一对全等的三角形(不再添加辅助线);
(2)选择你在(1)中写出的全等三角形中的任意一对进行证明.
24.(本题6分)
现将三张形状、大小完全相同的平行四边形透明纸片,分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形纸片的每个顶点与小正方形的顶点重合(如图1、图2、图3).
分别在图1、图2、图3中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,并把这两部分重新拼成符合下列要求的几何图形.
要求:
(1)在左边的平行四边形纸片中画一条裁剪线,然后在右边相对应的方格纸中,按实际大小画出所拼成的符合要求的几何图形;
(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙;
(3)所画出的几何图形的各顶点必须与小正方形的顶点重合.

25.(本题8分)
据2007年5月26日《生活报》报道,我省有关部门要求各中小学要把“每天锻炼一小时”写入课表.为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?

26.(本题8分)
青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价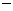 进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
(3)在“五?一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
打折前一次性购物总金额
优惠措施
不超过300元
不优惠
超过300元且不超过400元
售价打九折
超过400元
售价打八折
按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
27.(本题10分)
如图1,在正方形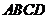 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
,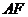 平分
平分 ,交
,交 于点
于点 .
.
(1)求证: ;
;
(2)点 从点
从点 出发,沿着线段
出发,沿着线段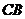 向点
向点 运动(不与点
运动(不与点 重合),同时点
重合),同时点 从点
从点 出发,沿着
出发,沿着 的延长线运动,点
的延长线运动,点 与
与 的运动速度相同,当动点
的运动速度相同,当动点 停止运动时,另一动点
停止运动时,另一动点 也随之停止运动.如图2,
也随之停止运动.如图2, 平分
平分 ,交
,交 于点
于点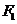 ,过点
,过点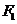 作
作 ,垂足为
,垂足为 ,请猜想
,请猜想 ,
, 与
与 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当 ,
,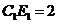 时,求
时,求 的长.
的长.

28.(本题10分)
如图,梯形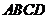 在平面直角坐标系中,上底
在平面直角坐标系中,上底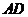 平行于
平行于 轴,下底
轴,下底 交
交 轴于点
轴于点 ,点
,点 (4,
(4,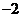 ),点
),点 ,
,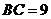 ,
, .
.
(1)求直线 的解析式;
的解析式;
(2)若点 的坐标为
的坐标为 ,动点
,动点 从
从 出发,以1个单位/秒的速度沿着
出发,以1个单位/秒的速度沿着 边向
边向 点运动(点
点运动(点 可以与点
可以与点 或点
或点 重合),求
重合),求 的面积
的面积 (
( )随动点
)随动点 的运动时间
的运动时间 秒变化的函数关系式(写出自变量
秒变化的函数关系式(写出自变量 的取值范围);
的取值范围);
(3)在(2)的条件下,当 秒时,点
秒时,点 停止运动,此时直线
停止运动,此时直线 与
与 轴交于点
轴交于点 .另一动点
.另一动点 开始从
开始从 出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由
出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由 到
到 ,然后由
,然后由 到
到 ,再由
,再由 到
到 ,最后由
,最后由 回到
回到 (点
(点 可以与梯形的各顶点重合).设动点
可以与梯形的各顶点重合).设动点 的运动时间为
的运动时间为 秒,点
秒,点 为直线
为直线 上任意一点(点
上任意一点(点 不与点
不与点 重合),在点
重合),在点 的整个运动过程中,求出所有能使
的整个运动过程中,求出所有能使 与
与 相等的
相等的 的值.
的值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com