
2007年浙江金华中考数学试题
卷Ⅰ
一、选择题(本题有10小题,每题4分,共40分)
1.计算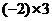 所得结果正确的是(
)
所得结果正确的是(
)
A.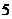 B.
B.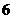 C.
C.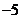 D.
D.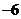
2.将抛物线 向上平移2个单位,得到抛物线的解析式是(
)
向上平移2个单位,得到抛物线的解析式是(
)
A. B.
B. C.
C. D.
D.
3.06年,我市深入实施环境污染整治,某经济开发区的40家化工企业中已关停、整改32家,每年排放的污水减少了167000吨.将167000用科学记数法表示为( )
A. B.
B. C.
C. D.
D.
4.如图是小玲在九月初九“重阳节”送给她外婆的礼盒,图中所示礼盒的主视图是( )

5.不等式 的解集在数轴上表示正确的是(
)
的解集在数轴上表示正确的是(
)

6.如图,点 都在⊙O上,若
都在⊙O上,若 ,则
,则 的度数为( )
的度数为( )

A. B.
B. C.
C. D.
D.
7.下列函数中,图象经过点 的反比例函数解析式是(
)
的反比例函数解析式是(
)
A. B.
B. C.
C. D.
D.
8.北京奥组委从

A.1500元 B.11张 C.5张 D.200元
9.国家级历史文化名城――金华,风光秀丽,花木葱茏.某广场上一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有 ,
, ,那么下列说法中错误的是(
)
,那么下列说法中错误的是(
)

A.红花、绿花种植面积一定相等
B.紫花、橙花种植面积一定相等
C.红花、蓝花种植面积一定相等
D.蓝花、黄花种植面积一定相等

A.0 B.
卷Ⅱ
二、填空题(本题有6小题,每题5分,共30分)
11. 的相反数是
.
的相反数是
.
12.分解因式: .
.
13.如图,直线 ,
, ,
, 为垂足.如果
为垂足.如果 ,那么
,那么 的度数是
°.
的度数是
°.

14.自由下落物体的高度 (米)与下落的时间
(米)与下落的时间 (秒)的关系为
(秒)的关系为 .现有一铁球从离地面
.现有一铁球从离地面 米高的建筑物的顶部作自由下落,到达地面需要的时间是
秒.
米高的建筑物的顶部作自由下落,到达地面需要的时间是
秒.
15.如图所示为一弯形管道,其中心线是一段圆弧 ,已知半径
,已知半径 ,
, ,则管道的长度(即
,则管道的长度(即 的长)为
cm.(结果保留
的长)为
cm.(结果保留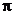 )
)

16.如图,在由24个边长都为1的小正三角形的网格中,点 是正六边形的一个顶点,以 点
是正六边形的一个顶点,以 点 为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长
.
为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长
.

三、解答题(本题有8小题,共80分,各小题都必须写出解答过程)
17.(本题8分)
18.(本题8分)
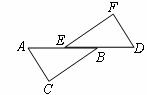
如图,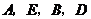 在同一直线上,在
在同一直线上,在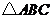 与
与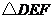 中,
中,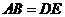 ,
,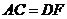 ,
,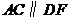 .
.
(1)求证: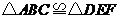 ;
;
(2)你还可以得到的结论是 (写出一个即可,不再添加其它线段,不再标注或使用其它字母).
19.(本题8分)
水果种植大户小方,为了吸引更多的顾客,组织了观光采摘游活动.每一位来采摘水果的顾客都有一次抽奖机会:在一只不透明的盒子里有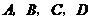 四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张.
四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张.
(1)请利用树状图(或列表)的方法,表示前后两次抽得的卡片所有可能的情况;
(2)如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?

20.(本题8分)
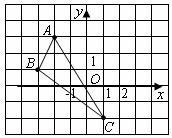
在直角坐标系中,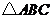 的三个顶点的位置如图所示.
的三个顶点的位置如图所示.
(1)请画出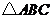 关于
关于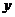 轴对称的
轴对称的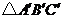 (其中
(其中 分别是
分别是 的对应点,不写画法);
的对应点,不写画法);
(2)直接写出 三点的坐标:
三点的坐标:
 .
.
21.(本题10分)
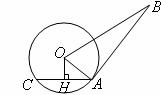
如图, 是⊙O的切线,
是⊙O的切线, 为切点,
为切点, 是⊙O的弦,过
是⊙O的弦,过 作
作 于点
于点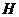 .若
.若 ,
,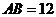 ,
, .
.
求:(1)⊙O的半径;
(2) 的值;
的值;
(3)弦 的长(结果保留两个有效数字).
的长(结果保留两个有效数字).
22.(本题12分)
光明中学七年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
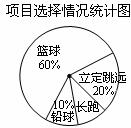

请你根据图表中的信息回答下列问题:
(1)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(2)求训练后篮球定时定点投篮人均进球数;
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加 .请求出参加训练之前的人均进球数.
.请求出参加训练之前的人均进球数.
23.(本题12分)
学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为 的小明
的小明 的影子
的影子 长是
长是 ,而小颖
,而小颖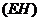 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方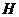 点,并测得
点,并测得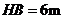 .
.
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置 ;
;
(2)求路灯灯泡的垂直高度 ;
;
(3)如果小明沿线段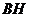 向小颖(点
向小颖(点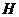 )走去,当小明走到
)走去,当小明走到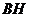 中点
中点 处时,求其影子
处时,求其影子 的长;当小明继续走剩下路程的
的长;当小明继续走剩下路程的 到
到 处时,求其影子
处时,求其影子 的长;当小明继续走剩下路程的
的长;当小明继续走剩下路程的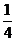 到
到 处,…按此规律继续走下去,当小明走剩下路程的
处,…按此规律继续走下去,当小明走剩下路程的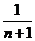 到
到 处时,其影子
处时,其影子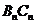 的长为
m(直接用
的长为
m(直接用 的代数式表示).
的代数式表示).

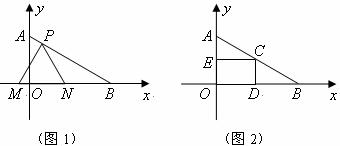
24.(本题14分)
如图1,在平面直角坐标系中,已知点 ,点
,点 在
在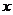 正半轴上,且
正半轴上,且 .动点
.动点 在线段
在线段 上从点
上从点 向点
向点 以每秒
以每秒 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为 秒.在
秒.在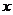 轴上取两点
轴上取两点 作等边
作等边 .
.
(1)求直线 的解析式;
的解析式;
(2)求等边 的边长(用
的边长(用 的代数式表示),并求出当等边
的代数式表示),并求出当等边 的顶点
的顶点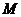 运动到与原点
运动到与原点 重合时
重合时 的值;
的值;
(3)如果取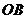 的中点
的中点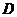 ,以
,以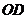 为边在
为边在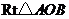 内部作如图2所示的矩形
内部作如图2所示的矩形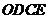 ,点
,点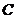 在线段
在线段 上.设等边
上.设等边 和矩形
和矩形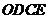 重叠部分的面积为
重叠部分的面积为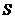 ,请求出当
,请求出当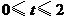 秒时
秒时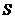 与
与 的函数关系式,并求出
的函数关系式,并求出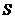 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com