
2007年临沂市费县初中调研考试
八年级数学试题
一、选择题(本题共15小题,每小题3分,共45分)
1.下列函数中,y是x的正比例函数的是
A.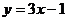 B.
B. C.
C. D.
D.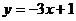
2.在扇形统计图中,某部分占总体的百分比为25%,则该部分所对的扇形圆心角为
A.120 ° B 90° C.60° D.50°
3.如图,O是AC、BD的中点,如果两个全等三角形为一组,那么全等三角形的组数是

A.1
B.
4.下列图形中,不是轴对称图形的是
A.等边三角形 B.等腰三角形 C.不等边三角形 D.线段
5.下列计算错误的是
A.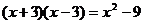 B.
B.
C.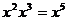 D.
D.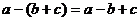
6.把分式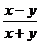 中的x、y都扩大5倍,则分式的值
中的x、y都扩大5倍,则分式的值
A.扩大25倍
B.扩大5倍 C.不变
D.缩小到原来的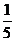
7.化简 的结果是
的结果是
A.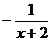 B.
B.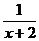 C.
C.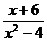 D.
D.
8.下列命题正确的是
A.等腰梯形的对角线相等且互相平分
B.一边上的两个角相等的梯形是等腰梯形
C.对角线相等且互相垂直的四边形是矩形
D.既是矩形,又是菱形的四边形是正方形
9.已知反比例函数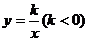 的图象上有两点A(
的图象上有两点A(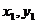 ),B(
),B( ),且
),且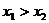 ,则
,则 的值是
的值是
A.正数 B.负数 C.非正数 D.不能确定
10.已知直角三角形的三边分别是3,4,x,则以x为边长的正方形的面积是
A.25
B.
11.三角形的三边长为a,b,c,且满足(a+b)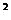 一c
一c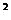 =2ab,则这个三角形的形状为
=2ab,则这个三角形的形状为
A.直角三角形 B.等腰三角形 C.锐角三角形 D.钝角三角形
12.下列四个等式① ;②
;② ;③
;③ ;④
;④ ,其中正确的个数是
,其中正确的个数是
A.0
B.
13.在数学活动课上,王老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是
A.测量对角线是否相等 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量其中三个角是否都为直角
14.某校五个绿化小组一天植树的棵数如下:l0,10,12,x,8,已知这组数据的众数与平均数相等,那么这组数据的中位数是
A 8
B.
15.一个样本数据是11个连续的自然数,那么下列结论一定正确的是
A.它的平均数是6 B.它的中位数是6
C.它的方差是5 D.它的方差是10
二、填空题(本题共5小题,每小题3分,共15分)将正确答案直接填在题中横线上
16.因式分解: .
.
17.当x=
时,分式 有意义.
有意义.
18.已知一个等腰三角形的腰长为
为 .
19.写出一个图象位于第一、三象限的反比例函数的解析式 .
20.已知关于x的方程 的解是正数,则m的取值范围是
.
的解是正数,则m的取值范围是
.
三、解答题(本题共60分)
21.(8分)为了了解八年级男生的身高情况,现随机抽取其中一所学校的60名男生(八年级),并对其身高测量后分别制表如下:
分组
147.5―155.5
155.5一l63.5
163.5―l71.5
171.5―179.5
频数
6
21
a
b
频率
c
d
e
0.1
测量完,制作好表格后,由于一名同学不小心打翻了一瓶墨汁,污染了表格(标有 a,b,c,d,e的五处被污染,其他三处没有被污染),调查组准备重新召集这60名男生测一次,小明同学看了看这张污染的表格说:“老师,不用重测了!我可以将这张表格复原。”小明能办到吗?a,b,c,d,e分别是什么?
22.(8分)P是等边三角形ABC内的一点,连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ,观察并猜想AP与CQ之间的大小关系,并证明你的结论.

23.(10分)骑自行车比步行每小时快
24.(10分)水池中有水若干吨,若单开一个出水口,水流速度v与全池水放光所用时间t如下表:
用时t(小时)
10
5

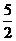
2

1
…… 逐渐减少
逐渐减少
出水速度v
(吨/小时)
l
2
3
4
5
8
10
…… 逐渐增大
逐渐增大
(1)①根据表中的数据在直角坐标系中描出实数对(t,v)的对应点;
②通过描点、连线、猜测、验证等方法确定v与t之间的函数关系式,并画出图象.
③当出水速度为每小时20吨时,多少小时可放完池中的水?
25.(12分)某校要从王聪和李明两名同学中挑选一人参加全国数学竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:

根据上表解答下列问题
(1)完成下表;
姓名
极差(分)
平均分
中位数(分)
众数(分)
方差
王聪
40
80
75
75
190
李明
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则王聪、李明在这五次测试中的优秀率分别是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获得奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由?
26.(12分)如图,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起,现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.

(1)如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM、FN的长度,猜想BM、FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com