
2008年贵阳市中考模拟试卷五
数 学
一、选择题(以下每小题都有A、B、C、D四个选项,其中只有一个选项正确,请把正确选项的字母选入该题的括号内,每小题4分,共20分)
1.下列计算中,正确的是( ).
A.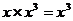 B.
B.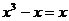
C.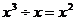 D.
D.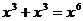
2.以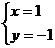 为解的二元一次方程组是( ).
为解的二元一次方程组是( ).
A.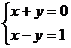 B.
B.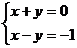
C.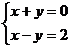 D.
D.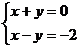
3.小明由A点出发向正东方向走10米到达B点,再由B点向东南方向走10米到达C点,则正确的是( ).
A.∠ABC=22.5° B.∠ABC=45°
C.∠ABC=67.5° D.∠ABC=135°
4.下图背景中的点均为大小相同的小正方形的顶点。其中画有两个四边形.下列叙述中正确的是( ).
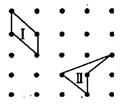
A.这两个四边形面积和周长都不相同
B.这两个四边形面积和周长都相同
C.这两个四边形有相同的面积,但I的周长大于Ⅱ的周长
D.这两个四边形有相同的面积,但I的周长小于Ⅱ的周长
5.将三粒均匀的分别标有1,2,3,4,5,6的正六面体骰子同时掷出,出现的数字分别为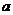 、b、c,则
、b、c,则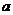 、b、c正好是直角三角形三边长的概率是( )
、b、c正好是直角三角形三边长的概率是( )
A.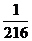 B.
B.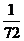 C.
C.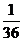 D.
D.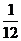
二、填空题(每小题3分,共30分)
6.化简|一2 |=___________.
7.分解因式:4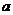 一
一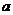 b2=____________________.
b2=____________________.
8.计算: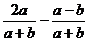 =________________.
=________________.
9.一个等腰三角形的一个外角等于70°,则这个三角形的三个角应该为________________.
10.改革开放以来,我国教育事业快速发展,去年普通高校招生人数达540万人,用科学记数法表示540万人为________________人.
11.两圆有多种位置关系,下图中不存在的位置关系是________________。
12.在一节综合课上,八名同学做手工的数量(单位:件)分别为:3,6,5,2,3,4,3,6,那么,这组数据的中位数是________________.
13.如图所示为一弯形管道,其中心线上一段圆弧AB.已知半径OA=60cm,∠AOB=108°,则管道的长度(即弧AB的长)为________________cm(结果保留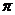 ).
).
14.有A(一3,一1)、B(1,1)、C(3,2)、D(4,3)四点,其中只有一点不在同一条直线上,这个点是________________.
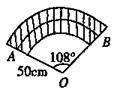
15.如图,点O是AC的中点,将周长为4cm的菱形ABCD沿对角线AC方向平移AO长度得到菱形OB’C’D’,则四边形OECF的周长是________________cm.
三、解答题
16.(本题9分),
在直角坐标系中,△ABC的三个顶点的位置如图所示.
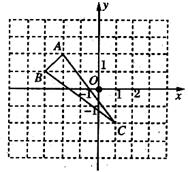
(1)请画出△ABC关于y轴对称的AA’B’C’(其中A’、B’、C’分别是A、B、C的对应点,不写作法);(6分)
(2)直接写出A’、B’、C’三点的坐标:A’( )、B’( )、C’( ).(3分)
17.(本题7分)
下图是一个食品包装盒的侧面展开图.
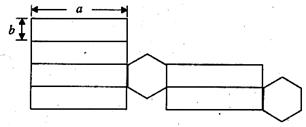
(1)请写出这个包装盒的多面体形状的名称;(2分)
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积(侧面积与两个底面积之和).(5分)
18.(本题13分)
数学课上,年轻的刘老师在讲授“轴对称”时,设计了如下四种教学方法:
①教师讲,学生听;②教师让学生自己做;③教师引导学生画图,发现规律;
④教师让学生对折纸,观察发现规律,然后画图.
数学教研组长将上述教学方法作为调研内容发到全年级8个班420名同学手中,要求每位同学选出自己最喜欢的一种.他随机抽取了60名学生的调查问卷,统计如图

(1)请将条形统计图补充完整,并计算扇形统计图中方法③的圆心角.(4分)
(2)全年级同学中最喜欢的教学方法是哪一种?选择这种教学方法的约有多少人?(4分)
(3)假如抽取的60名学生集中在某两个班,这个调查结果还合理吗?为什么?(3分)
(4)请你对老师的教学方法提出一条合理化的建议.(2分)
19.(本题10分)
几个同学准备在中考后到国家风景名胜区织金洞旅游,他们在中考前就包定了一辆最多可乘11人的面包车,其车费为480元.中考期间,又有两位同学提出加入他们的旅游.这样,虽然包车费不变,但原来准备去旅游的同学每人承担的车费少了12元,请问原来准备去织金洞旅游的有几个同学?
20.(本题10分)
如图,在四边形ABCD中,点E、F分别是AD、BC的中点,G、H分别是BD、AC的中点.
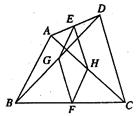
(1)求证:四边形EGFH是平行四边形;(5分)
(2)当AB、CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.(5分)
21.(本题12分)
某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.
(1)符合公司要求的购买方案有哪几种?请说明理由.(6分)
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元.假设新购买的这10辆车每日都可租出,要使这10辆车的日租金收入不低于1500元,那么应选择哪种方案?(6分)
22.(本题8分)
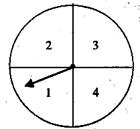
“六一”儿童节前夕,我市某县“关心下一代工作委员会”决定对品学兼优的“留守儿童”进行表彰.某校八年级8个班中只能选两个班级参加这项活动,且8(1)班必须参加。另外再从其他班级中选一个班参加活动.8(5)班有学生建议采用如下的方法:将一个带着指针的圆形转盘分成面积相等的4个扇形,并在每个扇形上分别标上1,2,3,4四个数字,转动转盘两次,将两次指针所指的数字相加,(当指针指在某一条等分线上时视为无效,重新转动)和为几就选哪个班参加,你认为这种方法公平吗?请说明理由.
23.(本题9分)
如图,P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为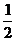 的半圆后得到图形P2,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3,P4,…,Pn,记纸板Pn的面积为Sn.
的半圆后得到图形P2,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3,P4,…,Pn,记纸板Pn的面积为Sn.

(1)试计算求出S2和S3(4分)
(2)猜测得到Sn一Sn-1=____________.(n≥2)(5分)
24.(本题10分)
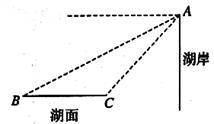
如图,某人在湖岸边A处发现一只小船在B处,其俯角为32°,过一会此船向岸边大约前进了10米到C处.其俯角为47°.求点A到湖面的距离.(精确到l米)
25.(本题12分)
善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间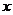 (单位:分钟)与学习收益量y的关系如左图所示,用于回顾反思的时间
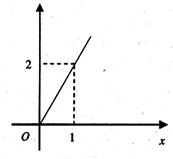
(单位:分钟)与学习收益量y的关系如左图所示,用于回顾反思的时间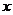 (单位:分钟)与学习收益量y的关系如下图所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(单位:分钟)与学习收益量y的关系如下图所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
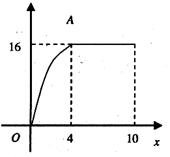
(1)求小迪解题的学习收益量y与用于解题的时间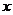 之间的函数关系式;(4分)
之间的函数关系式;(4分)
(2)求小迪回顾反思的学习收益量y与用于回顾反思的时间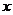 的函数关系式;(4分)
的函数关系式;(4分)
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?(4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com