
2007-2008学年度台儿庄九年级素能检测
数学试题
温馨提示:
亲爱的同学你好!请你仔细审题,认真答题,发挥自己的正常水平,轻松一点,相信自己的实力!
说明:
1、不可以使用计算器,未注明精确度的计算问题不得采取近似计算。
2、本试卷满分120分,在120分钟内完成。
卷I(选择题 36分)
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1、下列运算正确的是 ( )
A、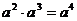 B、
B、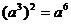 C、
C、 D、
D、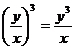
2、已知小明家距离学校10千米,而小蓉家距离小明家
A、3<d<10 B、3≤d≤
3、如图,已知AB∥CD。则
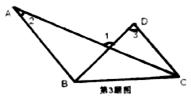
A、∠1=∠2+∠3 B、∠1=2∠2+∠3
C、∠1=2∠2-∠3 D、∠1=180°-∠2-∠3
4、用相同的小正方体搭一个几何体,使得它的主视图和俯视图如图所示,则搭这样的几何体至少需要小正方体的个数是( )
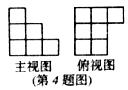
A、16个 B、12个 C、10个 D、8个
5、直线 经过第二、三、四象限,那么下列结论正确的是( )
经过第二、三、四象限,那么下列结论正确的是( )
A、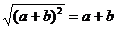 B、点(a,b)在第一象限内
B、点(a,b)在第一象限内
C、反比例函数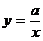 当
当 >0时,函数值
>0时,函数值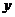 随
随 增大而减小
增大而减小
D、抛物线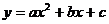 的对称轴过二、三象限
的对称轴过二、三象限
6、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )

A、25° B、30° C、45° D、60°
7、某商店的老板销售一种商品,他要以不低于进价20%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若你想买下标价为360元的这种商品,最多降价( ),商店老板才能出售.
A、80元 B、100元 C、120元 D、60元
8、根据图1和图2所示,对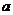 ,
,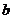 ,
,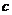 三种物体的重量判断不正确的是( )
三种物体的重量判断不正确的是( )

A、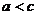 B、
B、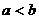 C、
C、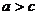 D、
D、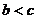
9、如图,在Rt△ABC中,AC=5,BC=12,⊙O分别与边AB、AC相切,切点分别为E、C,则⊙O的半径是 ( )
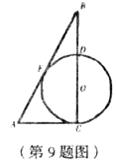
A、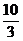 B、
B、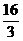 C、
C、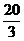 D、
D、
10、你手拿一枚硬币和一枚骰子,同时掷硬币和骰子,硬币出现正面、且骰子出现6的概率是 .
A、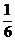 B、
B、 C、
C、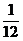 D、
D、
11、已知M、N两点关于y轴对称,且点M在双曲线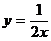 上,点N在直线
上,点N在直线 上,设点M的坐标为(
上,设点M的坐标为(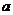 ,
,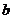 ),则二次函数
),则二次函数
A、有最小值,且最大值是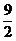 B、有最大值,且最大值是
B、有最大值,且最大值是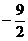
C、有最大值,且最大值是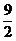 D、有最小值,且最小值是
D、有最小值,且最小值是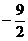
12、如图,在等腰梯形ABCD中,AD∥BC,AD=3,BC=5,AC,BD相交于O点,且∠BDC=60°,顺次连结等腰梯形各边中点所得四边形的周长是 ( )
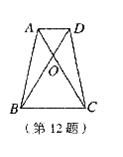
A、24 B、
第Ⅱ卷(非选择题 共84分)
二、填空题:本大题共6小题,共24分.只要求填写最后结果,每小题填对得4分。
13、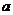 ,
,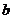 ,
,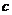 ,
,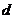 为实数,先规定一种新的运算:
为实数,先规定一种新的运算:
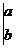
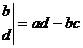 ,那么
,那么
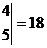 时,
时,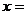
14、如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连结AP,PB,过点O分别作OE⊥AP于E,OF⊥PB于F,则EF= .

15、为了适应枣庄经济陕速发展的形势以及铁路运输和客流量大幅上升的需要,枣庄火车站扩建工程共投资73150000元.将73150000用科学记数法表示为 .
16、如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④△ADF∽△ECF.其中正确结论为 。(填序号)
CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④△ADF∽△ECF.其中正确结论为 。(填序号)

17、小亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立

18、如图,在平面直角坐标系中,二次函数 的图象过正方形ABOC的三个顶点A、B、C,则
的图象过正方形ABOC的三个顶点A、B、C,则 的值是
的值是

三、解答题:本大题共7小题,共60分.解答要写出必要的文字说明、证明过程或演算步骤.
19、(本题满分8分)解不等式组:
20、(本题满分8分)某网站公布了某城市一项针对2006年第一季度购房消费需求的随机抽样调查结果,下面是根据调查结果制作的购房群体可接受价位情况的比例条形统计图和扇形统计图的一部分.

请根据统计图中提供的信息回答下列问题:
(1)若2500~3000可接受价位所占比例是3500以上可接受价位所占比例的5倍,则这两个可接受价位所占的百分比分别为 .
(2)补全条形统计图和扇形统计图;
(3)购房群体中所占比例最大的人群可接受的价位是 ;
(4)如果2006年第一季度该市所有的有购房需求的人数为50000人,试估计这些有购房需求的人中可接受3500元/平方米以上的人数是 人.
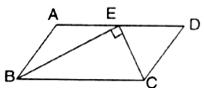
21、(本题满分8分)已知:如图,在平行四边形ABCD中,E是AD的中点,连结BE、CE,∠BEC=90°.
(1)求证:BE平分∠ABC;
(2)若EC=4,且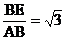 ,求四边形ABCE的面积。
,求四边形ABCE的面积。
22、(本题满分8分)A、B两城铁路长240千米,为使行使时间减少20分,需要提速10千米/时,但在现有条件下安全行驶限速100千米/时,问能否实现提速目标.
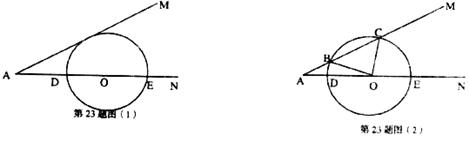
23、(本题满分8分)已知:∠MAN=30°,O为边AN上一点,以O为圆心、2为半径作⊙O,交AN于D、E两点,设AD= .
.
(1)如图(1)当 取何值时,⊙O与AM相切;
取何值时,⊙O与AM相切;
(2)如图(2)当 为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
24、(本题满分10分)如图,一元二次方程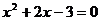 的二根
的二根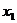 ,
,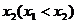 是抛物线
是抛物线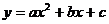 与
与 交点B,C的横坐标,且此抛物线过点A(3,6).
交点B,C的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式.
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标.
(3)在 轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.
轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.

25、(本题满分10分)如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4),点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直 轴于点P,连结AC交NP于Q,连结MQ.
轴于点P,连结AC交NP于Q,连结MQ.
(1)点 (填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量f的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com