
2008-2009学年度淄博市周村区第一学期九年级期中考试
数学试卷
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内)
1.如图,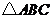 中
中 边上的高为
边上的高为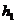 ,
,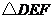 中
中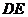 边上的高为
边上的高为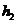 ,下列结论正确的是( )
,下列结论正确的是( )

A.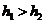 B.
B.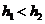 C.
C. D.无法确定
D.无法确定
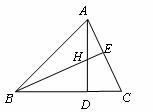
2.如图,在△ABC中,∠ABC=45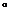 ,AC=4,H是高AD和BE的交点,则线段BH的长度是( )
,AC=4,H是高AD和BE的交点,则线段BH的长度是( )
A.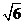 B.
B. D.5
D.5
3.科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
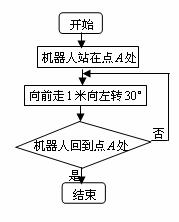
A.6米 B.8米 C.12米 D.不能确定
4.在△ABC中,∠C=90°,tanA= ,则sinB=( )
,则sinB=( )
A.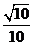 B.
B.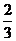 C.
C.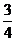 D.
D.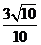
A. B.
B.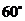
C.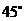 D.
D.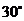
6.把抛物线y=x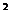 +bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x
+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x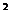 -3x+5,则( )
-3x+5,则( )
A.b=3,c=7 B.b=6,c=3
C.b=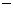 9,c=
9,c=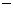 5 D.b=
5 D.b=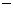 9,c=21
9,c=21
7.已知二次函数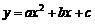 的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数
的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数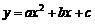 的图象上,则下列结论正确的是
的图象上,则下列结论正确的是
A.y1<y2<y3 B.y2<y1<y3
C.y3<y1<y2 D.y1<y3<y2
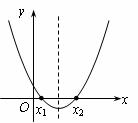
8.福娃们在一起探讨研究下面的题目:函数 (
(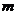 为常数)的图象如下图,如果
为常数)的图象如下图,如果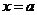 时,
时,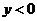 ;那么
;那么 时,函数值 参考下面福娃们的讨论,请你解该题,你选择的答案是( )
时,函数值 参考下面福娃们的讨论,请你解该题,你选择的答案是( )
贝贝:我注意到当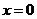 时,
时,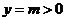 .
.
晶晶:我发现图象的对称轴为 .
.
欢欢:我判断出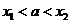 .
.
迎迎:我认为关键要判断 的符号.
的符号.
妮妮: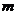 可以取一个特殊的值.
可以取一个特殊的值.
A.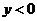 B.
B.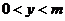 C.
C.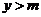 D.
D.
9.如下图,将一副三角板折叠放在一起,使直角的顶点重合于点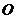 ,则
,则 ( )
( )
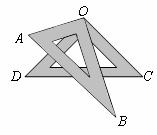
A.120º B.180º C.150º D.135º
10.如下图,在Rt△ABC中,∠C=900,∠A=300,E为AB上一点且AE:EB=4:1,
EF⊥AC于F,连结FB,则tan∠CFB的值等于( )
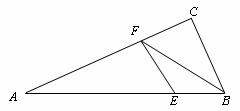
A. B.
B. 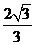 C.
C. 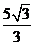 D.
D.
A.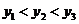 B.
B.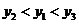
C.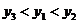 D.
D.
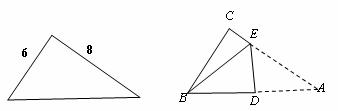
12.直角三角形纸片的两直角边长分别为6,8,现将△ABC如下图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 ( )
A. B.
B. C.
C. D.
D.
二、填空题
1.已知抛物线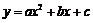 经过点A(5,0)、B(6,-6)和原点,则抛物线的函数关系式是
.
经过点A(5,0)、B(6,-6)和原点,则抛物线的函数关系式是
.
2.如下图,二次函数y=ax2+bx+c(a>0)与坐标轴交于点A、B、C且OA=1,OB=OC=3此二次函数的解析式为 .

3.如下图,所示的两条抛物线的解析式分别是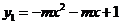 ,
,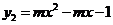 (其中m为常数,且
(其中m为常数,且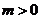 ).请写出三条与上述抛物线有关的不同类型的结论
;
).请写出三条与上述抛物线有关的不同类型的结论
;
; .

4.已知抛物线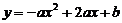 与
与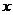 轴的一个交点为
轴的一个交点为 ,与y轴的正半轴交于点D.抛物线与
,与y轴的正半轴交于点D.抛物线与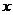 轴的另一个交点B的坐标是
轴的另一个交点B的坐标是

5.如图,在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,-1),二次函数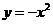 的图象为
的图象为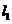 ,平移抛物线
,平移抛物线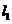 ,得到抛物线
,得到抛物线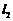 ,使
,使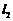 过点A,但不过点B,
过点A,但不过点B,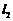 的顶点不是点A,请你写出抛物线
的顶点不是点A,请你写出抛物线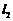 的一个解析式
(任写一个满足条件的即可). 平移抛物线
的一个解析式
(任写一个满足条件的即可). 平移抛物线 ,得到抛物线
,得到抛物线 ,使
,使 过点A,又过点B,请你写出抛物线
过点A,又过点B,请你写出抛物线 的一个解析式
的一个解析式

6.已知,点 在抛物线
在抛物线
则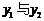 的大小关系是
的大小关系是
三、解答题
1.如下图是某宾馆大厅到二楼的楼梯设计图,已知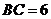 米,
米,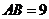 米,中间平台宽度
米,中间平台宽度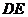 为2米,
为2米, 为平台的两根支柱,
为平台的两根支柱, 垂直于
垂直于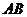 ,垂足分别为
,垂足分别为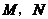 ,
, ,
,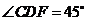 .
.
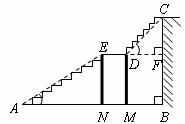
求 和
和 的水平距离
的水平距离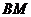 .(精确到0.1米,参考数据:
.(精确到0.1米,参考数据: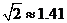 ,
,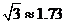 )
)
2.抛物线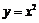 上有三点A、B、C,其横坐标分别是m、m+1、m+3,请你探究△ABC的面积S是否为定值,若是,请求出这个值;若不是,请你求出S与m的函数关系式.
上有三点A、B、C,其横坐标分别是m、m+1、m+3,请你探究△ABC的面积S是否为定值,若是,请求出这个值;若不是,请你求出S与m的函数关系式.
3.如图,在平面直角坐标系中,已知点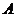 坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线
坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线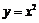 从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.

(1)求线段OA所在直线的函数解析式;
(2)设抛物线顶点M的横坐标为m,请用含m的代数式表示点P的坐标;
4.如下图,抛物线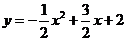 与x轴的交于A,B两点.点E(1,-1),以A、E为顶点作平行四边形AEMN,使点M,N都在抛物线上.
与x轴的交于A,B两点.点E(1,-1),以A、E为顶点作平行四边形AEMN,使点M,N都在抛物线上.
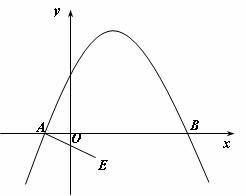
求点M,N的坐标.
5.如下图,抛物线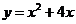 与x轴分别相交于点B、O,它的顶点为A,连接AB,AO
与x轴分别相交于点B、O,它的顶点为A,连接AB,AO
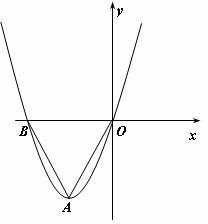
(1)求点A的坐标;
(2)以点A、B、O、P为顶点构造直角梯形,请求一个满足条件的顶点P的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com