
2008年丰台区初三毕业及统一练习
数学试卷
第Ⅰ卷 (共32分)
一、选择题(共8个小题,每小题4分,共32分)
1.-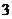 的相反数是
的相反数是
A.-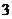 B.
B.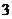 C.
C.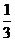 D.-
D.-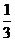
2.光年是天文学中的距离单位,1光年大约是95000000万千米.将95000000用科学记数法表示为
A.9.5×107 B.95×106
C.9.5×106 D.0.95×108
3.在正方形网格中,若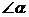 的位置如图所示,则
的位置如图所示,则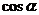 的值为
的值为

A.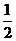 B.
B.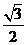
C.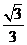 D.
D.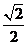
4.在函数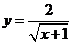 中,自变量
中,自变量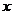 的取值范围是
的取值范围是
A.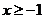 B.
B.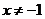 C.
C.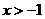 D.
D.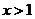
5.甲、乙两同学近期5次百米跑测试成绩的平均数相同,甲同学成绩的方差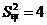 ,乙同学成绩的方差
,乙同学成绩的方差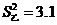 ,则下列对他们测试成绩稳定性的判断,正确的是
,则下列对他们测试成绩稳定性的判断,正确的是
A.甲的成绩较稳定 B.乙的成绩较稳定
C.甲、乙成绩稳定性相同 D.甲、乙成绩的稳定性无法比较
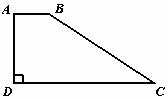
6.如图,在直角梯形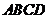 中,
中,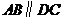 ,
,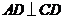 于点
于点 ,若
,若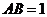 ,
, ,
,
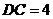 ,则
,则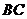 的长为
的长为
A.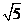 B.
B.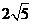
C.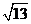 D.
D.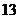
7.若方程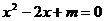 有两个不相等的实数根,则
有两个不相等的实数根,则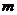 的取值范围是
的取值范围是
A.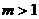 B.
B.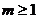 C.
C.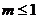 D.
D. 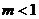
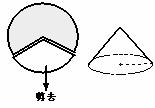
8.如图,如果将半径为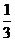 圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为
圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为
A.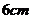 B.
B.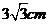
C.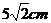 D.
D.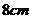
第Ⅱ卷 (共88分)
9.写出一个图像在第二、第四象限的反比例函数的解析式 .
10.在英语单词“Olympic Games”(奥运会)中任意选择一个字母,这个字母为“m”的概率是 .
11.如图,半径为5的⊙O中,如果弦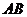 的长为8,那么圆心
的长为8,那么圆心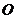 到
到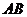 的距离,即
的距离,即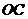 的长等于
.
的长等于
.
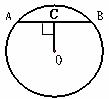
12.对于实数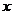 ,规定
,规定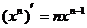 ,若
,若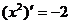 ,则
,则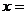 .
.
13.(本小题满分4分)
分解因式: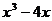 .
.
14.(本小题满分5分)
计算: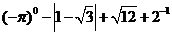 .
.
15.(本小题满分5分)
16.(本小题满分5分)
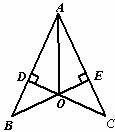
已知:如图,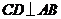 于点
于点 ,
,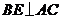 于点
于点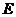 ,
,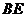 与
与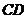 交于点
交于点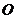 ,且
,且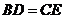 .
.
求证: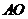 平分
平分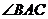 .
.
17.(本小题满分6分)
若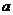 满足不等式组
满足不等式组 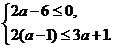 请你为
请你为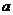 选取一个合适的数,使得代数式
选取一个合适的数,使得代数式
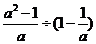 的值为一个奇数.
的值为一个奇数.
四.解答题:
18.(本小题满分5分)
某小区便利店老板到厂家购进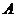 、
、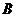 两种香油共
两种香油共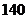 瓶,花去了
瓶,花去了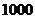 元.其进价和售价如下表:
元.其进价和售价如下表:
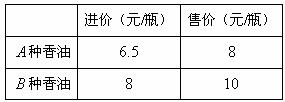
(1)该店购进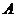 、
、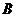 两种香油各多少瓶?
两种香油各多少瓶?
(2)将购进的 瓶香油全部销售完,可获利多少元?
瓶香油全部销售完,可获利多少元?
19.(本小题满分5分)
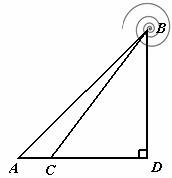
如图,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点处有人求救,便立即派三名救生员前去营救.1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑 点出发,他们在岸边跑的速度都是
点出发,他们在岸边跑的速度都是 .
.
五.解答题:
20.已知:如图,以 的边
的边 为直径的⊙O交边
为直径的⊙O交边 于点
于点 ,且过点
,且过点 的切线
的切线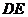 平分边
平分边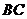 .
.
(1)求证: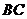 是⊙O的切线;
是⊙O的切线;
(2)当 满足什么条件时,以点
满足什么条件时,以点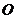 、
、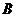 、
、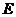 、
、 为顶点的四边形是正方形?请说明理由.
为顶点的四边形是正方形?请说明理由.
六.解答题
21.数学老师将相关教学方法作为调查内容发到全年级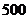 名学生的手中,要求每位学生选出自己喜欢的一种,调查结果如下列统计图所示:
名学生的手中,要求每位学生选出自己喜欢的一种,调查结果如下列统计图所示:
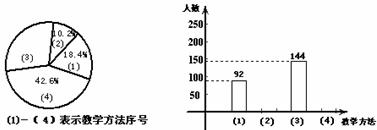
(1)请你将扇形统计图和条形统计图补充完整;
(2)写出学生喜欢的教学方法的众数;
(3)针对调查结果,请你发表不超过30字的简短评说。
七、解答题(本题满分5分)
22.一次函数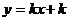 的图像经过点
的图像经过点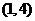 ,且分别与
,且分别与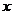 轴、
轴、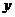 轴交于点
轴交于点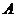 、
、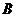 .点
.点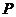
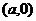 在
在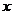 轴正半轴上运动,点
轴正半轴上运动,点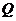
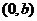 在
在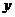 轴正半轴上运动,且
轴正半轴上运动,且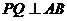 .
.
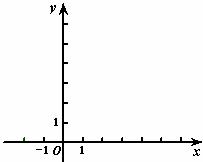
(1)求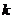 的值,并在给出的平面直角坐标系中画出该一次函数的图像;
的值,并在给出的平面直角坐标系中画出该一次函数的图像;
(2)求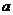 与
与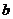 满足的等量关系式.
满足的等量关系式.
八.解答题:
23.某公司专销产品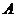 ,第一批产品
,第一批产品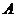 上市
上市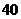 天恰好全部售完.该公司对第一批产品
天恰好全部售完.该公司对第一批产品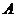 上市后的市场销售情况进行了跟踪调查,调查结果如图(1)和图(2)所示,其中图(1)中的折线表示的是市场日销售量
上市后的市场销售情况进行了跟踪调查,调查结果如图(1)和图(2)所示,其中图(1)中的折线表示的是市场日销售量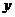 (万元)与上市时间
(万元)与上市时间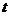 (天)的关系,图(2)中的折线表示的是每件产品
(天)的关系,图(2)中的折线表示的是每件产品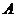 的日销售利润
的日销售利润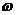 (元)与上市时间
(元)与上市时间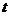 (天)的关系.
(天)的关系.
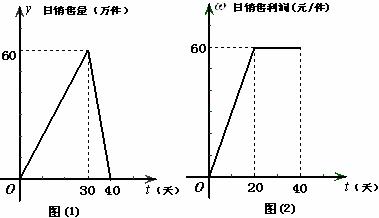
(1)试写出第一批产品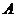 的市场日销售量
的市场日销售量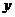 (万元)与上市时间
(万元)与上市时间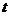 (天)的关系式;
(天)的关系式;
(2)第一批产品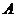 上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?
上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?
九.解答题:(8分)
24.有一座抛物线型拱桥,其水面宽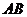 为
为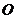 离水面
离水面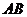 的距离
的距离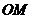 为
为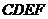 ,如图建立平面直角坐标系.
,如图建立平面直角坐标系.
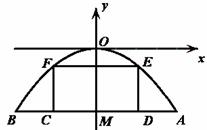
(1)求此抛物线的解析式,并写出自变量的取值范围;
(2)如果限定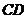 的长为
的长为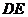 的长不能超过多少米,才能使船通过拱桥?
的长不能超过多少米,才能使船通过拱桥?
(3)若设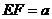 ,请将矩形
,请将矩形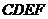 的面积
的面积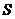 用含
用含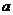 的代数式表示,并指出
的代数式表示,并指出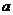 的取值范围.
的取值范围.
十.解答题:(8分)
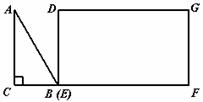
25.如图,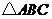 为直角三角形,
为直角三角形, ,
,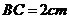 ,
,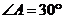 ;四边形
;四边形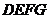 为矩形,
为矩形,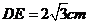 ,
,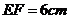 ,且点
,且点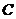 、
、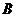 、
、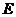 、
、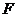 在同一条直线上,点
在同一条直线上,点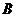 与点
与点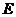 重合.
重合.
(1)求边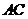 的长;
的长;
(2)将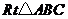 以每秒
以每秒 的速度沿矩形
的速度沿矩形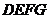 的边
的边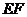 向右平移,当点
向右平移,当点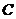 与点
与点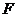 重合时停止移动,设
重合时停止移动,设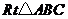 与矩形
与矩形 重叠部分的面积为
重叠部分的面积为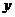 ,请求出重叠部分的面积
,请求出重叠部分的面积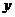 (
( )与移动时间
)与移动时间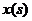 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);
(3)在(2)的基础上,当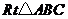 移动至重叠部分的面积为
移动至重叠部分的面积为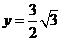
 时,将
时,将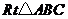 沿边
沿边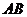 向上翻折,得到
向上翻折,得到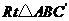 ,请求出
,请求出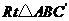 与矩形
与矩形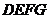 重叠部分的周长(可利用备用图).
重叠部分的周长(可利用备用图).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com