
2009年辽宁省抚顺市初中毕业生学业考试
数学试卷
考试时间120分钟 试卷满分150分
一、选择题(下列各题的备选答案中,只有一个是正确的.请将正确答案的选项填写在下表中相应题号下的空格内.每小题3分,共24分)
1.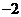 的相反数是( )
的相反数是( )
A.2 B.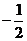 C.
C.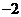 D.
D.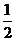
2.某市在一次扶贫助残活动中,共捐款2580000元.将2580000元用科学记数法表示为( )
A.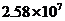 元 B.
元 B.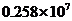 元 C.
元 C.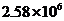 元 D.
元 D.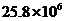 元
元
3.一个正方体的每个面都有一个汉字,其平面展开图如图所示,那么在该正方体中和“毒”字相对的字是( )
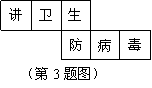
A.卫 B.防 C.讲 D.生
4.下列事件是必然事件的是( )
A.阴天一定会下雨
B.打开电视机,任选一个频道,屏幕上正在播放篮球比赛节目
C.某种彩票的中奖率为1%,买100张彩票一定中奖
D.13名学生中一定有两个人在同一个月过生日
5.下列运算正确的是( )
A.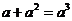 B.
B.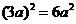 C.
C.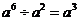 D.
D.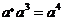
6.关于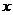 的二次函数
的二次函数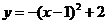 ,下列说法正确的是( )
,下列说法正确的是( )
A.图象的开口向上
B.图象的顶点坐标是(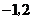 )
)
C.当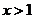 时,
时, 随
随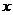 的增大而减小
的增大而减小
D.图象与 轴的交点坐标为(0,2)
轴的交点坐标为(0,2)
7.如图所示,已知点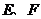 分别是
分别是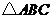 中
中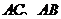 边的中点,
边的中点,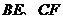 相交于点
相交于点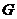 ,
,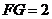 ,则
,则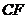 的长为( )
的长为( )
A.4 B.
8.如图所示,正方形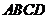 的面积为12,
的面积为12, 是等边三角形,点
是等边三角形,点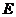 在正方形
在正方形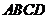 内,在对角线
内,在对角线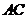 上有一点
上有一点 ,使
,使 的和最小,则这个最小值为( )
的和最小,则这个最小值为( )
A.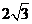 B.
B.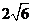 C.3 D.
C.3 D.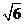
二、填空题(每小题3分,共24分)
9.一组数据4,3,5,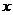 ,4,5的众数是4,则
,4,5的众数是4,则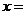 .
.
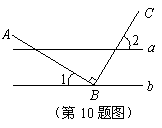
10.如图所示,直线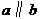 ,点
,点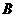 在直线
在直线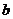 上,且
上,且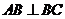 ,
,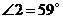 ,则
,则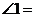 度.
度.
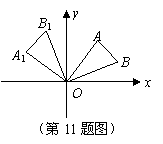
11.如图所示,在平面直角坐标系中, 三个顶点的坐标
三个顶点的坐标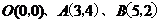 。将
。将 绕原点
绕原点 按逆时针方向旋转
按逆时针方向旋转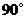 后得到
后得到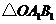 ,则点
,则点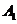 的坐标是
.
的坐标是
.
12.在反比例函数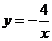 的图象上有两点
的图象上有两点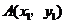 、
、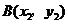 ,当
,当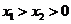 时,
时,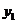 与
与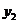 的大小关系是
.
的大小关系是
.
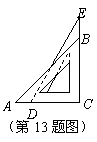
13.将一个含30°角的三角板和一个含45°角的三角板如图摆放,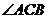 与
与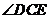 完全重合,
完全重合,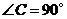 ,
,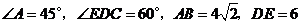 ,则
,则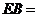 .
.

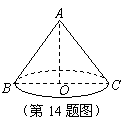
14.如图所示,已知圆锥的高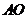 为
为 ,底面圆的直径
,底面圆的直径 长为
长为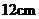 ,则此圆锥的侧面展开图的圆心角为
度.
,则此圆锥的侧面展开图的圆心角为
度.

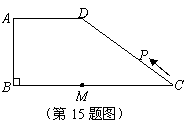
15.如图所示,在梯形 中,
中, ,点
,点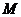 是线段
是线段 上一定点,且
上一定点,且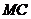 =8.动点
=8.动点 从
从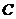 点出发沿
点出发沿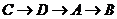 的路线运动,运动到点
的路线运动,运动到点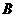 停止.在点
停止.在点 的运动过程中,使
的运动过程中,使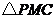 为等腰三角形的点
为等腰三角形的点 有 个.
有 个.

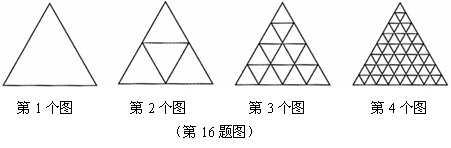
16.观察下列图形(每幅图中最小的三角形都是全等的),请写出第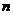 个图中最小的三角形的个数有
个.
个图中最小的三角形的个数有
个.

三、解答题(每题8分,共16分)
17.计算: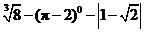 .
.
18.先化简,再对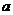 取一个你喜欢的数,代入求值.
取一个你喜欢的数,代入求值.
 .
.
四、解答题(每题10分,共20分)
19.某学校为了进一步丰富学生的体育活动,欲增购一些体育器材,为此对该校一部分学生进行了一次“你最喜欢的体育活动”的问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
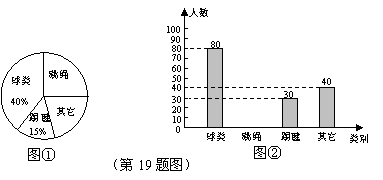

请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,一共抽查了 名学生;
(2)请将上面两幅统计图补充完整;
(3)图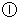 中,“踢毽”部分所对应的圆心角为
度;
中,“踢毽”部分所对应的圆心角为
度;
(4)如果全校有1860名学生,请问全校学生中,最喜欢“球类”活动的学生约有多少人?
20.如图所示,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘 ,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜。(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止)
,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜。(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止)

(1)用树状图或列表法求乙获胜的概率;
(2)这个游戏规则对甲乙双方公平吗?请判断并说明理由.
五、解答题(每题10分,共20分)
21.如图所示, 与
与 相切于点
相切于点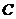 ,线段
,线段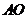 交
交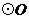 于点
于点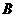 .过点
.过点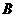 作
作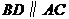 交
交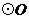 于点
于点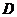 ,连接
,连接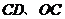 ,且
,且 交
交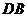 于点
于点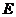 .若
.若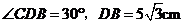 .
.


(1)求 的半径长;
的半径长;
(2)求由弦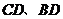 与弧
与弧 所围成的阴影部分的面积。(结果保留
所围成的阴影部分的面积。(结果保留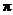 )
)
22.由于受甲型H1N1流感(起初叫猪流感)的影响,4月初某地猪肉价格大幅度下调,下调后每斤猪肉价格是原价格的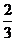 ,原来用60元买到的猪肉下调后可多买2斤。4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上调为每斤14.4元.
,原来用60元买到的猪肉下调后可多买2斤。4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上调为每斤14.4元.
(1)求4月初猪肉价格下调后每斤多少元?
(2)求5、6月份猪肉价格的月平均增长率.
六、解答题(每题10分,共20分)
23.如图所示,已知: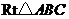 中,
中,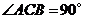 .
.


(1)尺规作图:作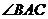 的平分线
的平分线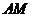 交
交 于点
于点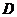 (只保留作图痕迹,不写作法);
(只保留作图痕迹,不写作法);
(2)在(1)所作图形中,将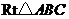 沿某条直线折叠,使点
沿某条直线折叠,使点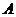 与点
与点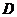 重合,折痕
重合,折痕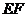 交
交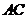 于点
于点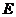 ,交
,交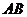 于点
于点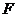 ,连接
,连接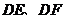 ,再展回到原图形,得到四边形
,再展回到原图形,得到四边形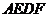 .
.
①试判断四边形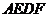 的形状,并证明;
的形状,并证明;
②若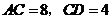 ,求四边形
,求四边形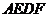 的周长和
的周长和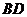 的长.
的长.
24.某食品加工厂,准备研制加工两种口味的核桃巧克力,即原味核桃巧克力和益智核桃巧克力.现有主要原料可可粉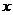 块.
块.
(1)求该工厂加工这两种口味的巧克力有哪几种方案?
(2)设加工两种巧克力的总成本为 元,求
元,求 与
与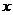 的函数关系式,并说明哪种加工方案使总成本最低?总成本最低是多少元?
的函数关系式,并说明哪种加工方案使总成本最低?总成本最低是多少元?
七、解答题(本题12分)
25.已知:如图所示,直线 与
与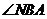 的平分线交于点
的平分线交于点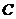 ,过点
,过点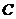 作一条直线
作一条直线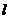 与两条直线
与两条直线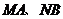 分别相交于点
分别相交于点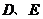 .
.
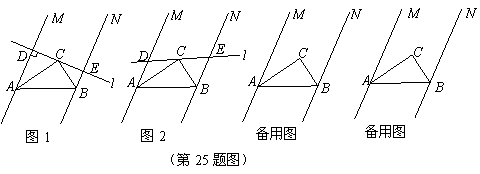

(1)如图1所示,当直线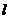 与直线
与直线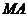 垂直时,猜想线段
垂直时,猜想线段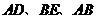 之间的数量关系,请直接写出结论,不用证明;
之间的数量关系,请直接写出结论,不用证明;
(2)如图2所示,当直线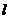 与直线
与直线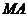 不垂直且交点
不垂直且交点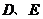 都在
都在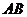 的同侧时,(1)中的结论是否成立?如果成立,请证明:如果不成立,请说明理由;
的同侧时,(1)中的结论是否成立?如果成立,请证明:如果不成立,请说明理由;
(3)当直线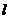 与直线
与直线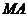 不垂直且交点
不垂直且交点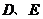 在
在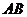 的异侧时,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,那么线段
的异侧时,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,那么线段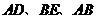 之间还存在某种数量关系吗?如果存在,请直接写出它们之间的数量关系.
之间还存在某种数量关系吗?如果存在,请直接写出它们之间的数量关系.
八、解答题(本题14分)
26.已知:如图所示,关于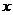 的抛物线
的抛物线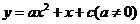 与
与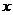 轴交于点
轴交于点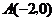 、点
、点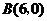 ,与
,与 轴交于点
轴交于点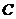 .
.
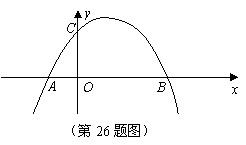

(1)求出此抛物线的解析式,并写出顶点坐标;
(2)在抛物线上有一点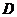 ,使四边形
,使四边形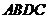 为等腰梯形,写出点
为等腰梯形,写出点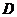 的坐标,并求出直线
的坐标,并求出直线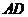 的解析式;
的解析式;
(3)在(2)中的直线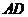 交抛物线的对称轴于点
交抛物线的对称轴于点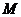 ,抛物线上有一动点
,抛物线上有一动点 ,
,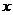 轴上有一动点
轴上有一动点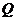 .是否存在以
.是否存在以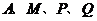 为顶点的平行四边形?如果存在,请直接写出点
为顶点的平行四边形?如果存在,请直接写出点 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com