
2009-2010学年度济宁市嘉祥第一学期初三期中考试
数学试卷
一.相信你一定能选对!(每题3分,共36分)
1.在艺术字中,有些汉字或字母是对称图形,但下面的汉字或字母只是中心对称图形的是
( )


2.已知△ABC内接于⊙O,∠BOC=100°,则∠A=( )
A.50° B.130° C.50°或100° D.50°或130°
3.⊙O1与⊙O2的半径分别是4和5,若O1O2=10,则这两圆的位置关系( )
A.外离 B.外切 C.相交 D.内切
4.关于 的方程
的方程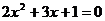 .下列结论正确的是( )
.下列结论正确的是( )
A.有2个不相等的实数根 B.没有实数根
C.有2个相等的实数根 D.不能确定
5.已知Rt△ABC中,∠C=90°,AC=3厘米,BC=4厘米,CD⊥AB于D,以C为圆心,以2.4厘米为半径画⊙C,则点D与⊙C的位置关系是( )
A.D在⊙C内 B.D在⊙C上
C.D在⊙C外 D.无法确定
6.关于 的方程
的方程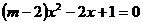 有实数解,那么
有实数解,那么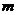 的取值范围是( )
的取值范围是( )
A.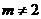 B.
B.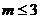
C.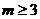 D.
D.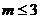 且
且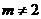
7.某化工厂今年一月份生产化工原料15万吨,通过优化管理,产量逐年上升,第一季度共生产化工原料60万吨,设二、三月份平均增长的百分率相同,均为 ,可列出方程为( )
,可列出方程为( )
A.15(1+ )=60 B.15(1+
)=60 B.15(1+ )2=60
)2=60
C.15+15(1+ )2=60 D.15+15(1+
)2=60 D.15+15(1+ )+15(1+
)+15(1+ )2=60
)2=60
8.以1+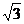 与1-
与1-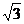 为根的一元二次方程的是( )
为根的一元二次方程的是( )
A. 2+2
2+2 +2=0 B.
+2=0 B. 2-2
2-2 +2=0
+2=0
C. 2-2
2-2 -2=0 D.
-2=0 D. 2+2
2+2 -2=0
-2=0
9.使式子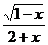 有意义的
有意义的 的取值范围是(
)
的取值范围是(
)
A.
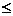 1 B.
1 B.
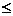 1或
1或 ≠
≠
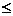 1且
1且 ≠-2 D.
≠-2 D. <1且
<1且 ≠-2
≠-2
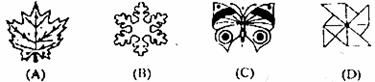
10.下列平面图形中,既是轴对称图形,又是中心对称图形的是( )
11.下列二次根式中,最简二次根式是( )
A.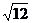
 B.
B.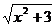 C.
C.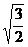 D.
D.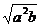
12.方程 2+6
2+6 -5=0的左边配成完全平方后所得方程为( )
-5=0的左边配成完全平方后所得方程为( )
A.( +3)2=14 B.(
+3)2=14 B.( -3)2=
-3)2= +3)2=4 D.(
+3)2=4 D.( -3)2=4
-3)2=4
二.耐心填一填(每题3分,共18分)
13.关于 的方程
的方程 2-
2-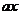 -
-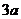 =0的一个根是-2,则它的另一个根是_______。
=0的一个根是-2,则它的另一个根是_______。
14.在半径为2的⊙O中,弦AB的长为2,则弦AB所对的圆周角的度数为______。
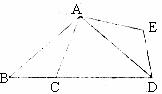
15.如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至在△ADE处,使点B落在BC的延长线上的D点处,则∠BDE=______ 度。
16.若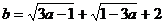 ,则
,则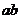 的等于______
的等于______
17.圆O的半径为
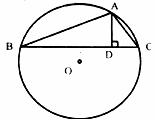
18.如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动时,始终与AB相交,记点A、B到MN的距离分别为h1、h2,则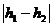 等于______。
等于______。

三.解答题
19.解下列方程(每小题4分,共8分)
(1) 2-7
2-7 +6=0(因式分解法) (2)2
+6=0(因式分解法) (2)2 (
( +4)=1(求根公式法)
+4)=1(求根公式法)
20.化简与计算(每小题4分,共8分)
(1)4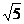 +
+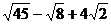 (2)
(2)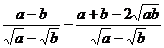
21.(1)(本题5分)在解方程 2+p
2+p +q=0时,小张看错了p,解得方程的根为1与-3;小王看错了q,解得方程的根为4与-2,这个方程的根应该是什么?
+q=0时,小张看错了p,解得方程的根为1与-3;小王看错了q,解得方程的根为4与-2,这个方程的根应该是什么?
(2)(本题5分)方程 2-2
2-2 -4=0的两根为
-4=0的两根为 1、
1、 2,求
2,求 1-
1- 2的值。
2的值。
22.(8分)已知:如图,AB是⊙O的直径,E是⊙O上一点,C是 的中点.弦CD⊥AB于K,交弦AE于G、BC交AE于F,
的中点.弦CD⊥AB于K,交弦AE于G、BC交AE于F,
(1)求证:CG=AG
(2)求证:△CFG是等腰三角形。

23.(8分)某商场将进货价为30元的台灯以40元售出,平均每月能售出600个。调查表明,这种台灯的售价每上涨1元,其销售量将减少10个,为了实现平均每月10000元销售利润,这种台灯的售价应定为多少,这时应进多少个台灯?
24.(9分)如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为△ABC内一点,AD=1,而DC、DB的长是关于 的方程
的方程 +6=0的两个实数根
+6=0的两个实数根 1,
1, 2(DC<DB)并且
2(DC<DB)并且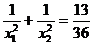
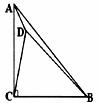
(1)作出△ACD绕点C顺时针旋转90°后所得△BCE。
(2)求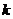 的值.并连结DE并说明△BDE的形状;
的值.并连结DE并说明△BDE的形状;
(3)求∠ADC的度数。
25.(7分)在钝角△ABC中,AD⊥BC,垂足为点D,且AD与CD(AD>CD)的长度为方程 2-7
2-7 +12=0的两根,⊙O是△ABC的外接圆.
+12=0的两根,⊙O是△ABC的外接圆.
(1)求AC值:
(2)若∠B=15°,求⊙O的面积.
26、(8分)观察下列各式及其变形过程:
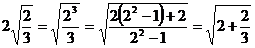
(1)按上述等式及其验证过程的基本思路,猜想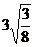 的变形结果并进行证明。
的变形结果并进行证明。
(2)针对上述各式反映的规律,写出用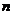 (
(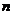 为自然数,
为自然数,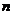 ≥2)表示的算式,并证明。
≥2)表示的算式,并证明。
(3)依上面规律,写出用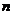 表示下列各式的规律:
表示下列各式的规律:
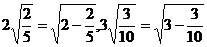 ……(不要求证明)
……(不要求证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com