
珠海市2008年高三模拟考试
数 学(理 科)试卷 2007.1.4
本试卷共4页,21小题,满分150分.考试用时120分钟.
注意事项:1.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
2.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合 ,
,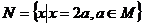 ,则集合
,则集合
A. B.
B.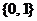 C.
C. D.
D.
2.设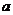 是实数,且
是实数,且 是实数,则
是实数,则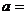
A. B.
B.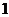 C.
C. D.
D.
3.已知函数 (其中
(其中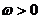 ,
,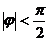 )的最小正周期是
)的最小正周期是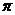 ,且
,且 ,则
,则
A. ,
,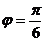 B.
B. ,
,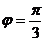
C. ,
,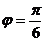 D.
D. ,
,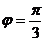
4.下列四个命题中,真命题的个数为
(1)如果两个平面有三个公共点,那么这两个平面重合;
(2)两条直线可以确定一个平面;
(3)若 ,
, ,
, ,则
,则 ;
;
(4)空间中,相交于同一点的三直线在同一平面内.
A.1 B.
5.已知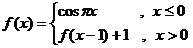 ,则
,则 的值为
的值为
A. B.
B. C.1 D.2
C.1 D.2
6.设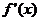 是函数
是函数 的导函数,将
的导函数,将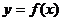 和
和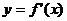 的图像画在同一个直角坐标系中,不可能正确的是
的图像画在同一个直角坐标系中,不可能正确的是




A. B. C. D.
7.设 ,
, 分别为具有公共焦点
分别为具有公共焦点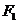 与
与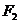 的椭圆和双曲线的离心率,
的椭圆和双曲线的离心率,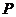 为两曲线的一个公共点,且满足
为两曲线的一个公共点,且满足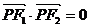 ,则
,则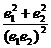 的值为
的值为
A. B.1 C.2 D.不确定
B.1 C.2 D.不确定
8.已知 ,
,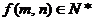 (
( 、
、 ,且对任意
,且对任意 、
、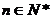 都有:
都有:
① ;②
;②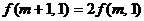 .
.
给出以下三个结论:(1) ;(2)
;(2) ;(3)
;(3)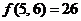 .
.
其中正确的个数为
A.3 B.2 C.1 D.0
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
9.圆心为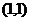 且与直线
且与直线 相切的圆的方程是_______________.
相切的圆的方程是_______________.
10.向量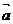 、
、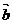 满足
满足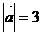 ,
, ,
, ,则
,则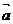 、
、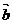 的夹角为________.
的夹角为________.
11.若把英语单词“good”的字母顺序写错了,则可能出现的错误共有________种.
 12.如右图,一个空间几何体的主视图、左视图是周长为4一个内角为
12.如右图,一个空间几何体的主视图、左视图是周长为4一个内角为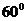 的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为________.
的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为________.
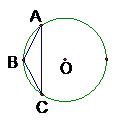
13.(坐标系与参数方程选做题)极坐标系下,直线
 与圆
与圆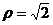 的公共点个数是________.
的公共点个数是________.
 14.(不等式选讲选做题)
14.(不等式选讲选做题) 、
、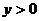 ,
,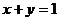 ,则
,则 的最小值为______.
的最小值为______.
15.(几何证明选讲选做题)如图所示,等腰三角形 的底边
的底边 长
长
为6 , 其外接圆的半径长为5, 则三角形 的面积是________.
的面积是________.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
设集合 ,
, .
.
(1)求集合 ;
;
(2)若不等式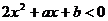 的解集为
的解集为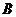 ,求
,求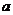 ,
,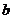 的值.
的值.
17.(本小题满分12分)
已知函数 .
.
(1)求 的最值;
的最值;
(2)求 的单调增区间.
的单调增区间.
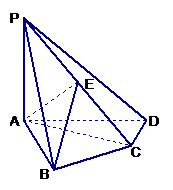
18.(本小题满分14分)
如图,四棱锥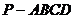 中,
中, 底面
底面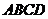 ,
,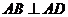 ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
(1)求证: ;
;
(2)求证: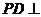 面
面 ;
;
(3)求二面角 的平面角的正弦值.
的平面角的正弦值.
19.(本小题满分14分)
已知抛物线 (
(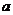 为非零常数)的焦点为
为非零常数)的焦点为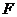 ,点
,点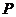 为抛物线
为抛物线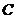 上一个动点,过点
上一个动点,过点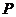 且与抛物线
且与抛物线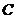 相切的直线记为
相切的直线记为 .
.
(1)求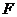 的坐标;
的坐标;
(2)当点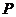 在何处时,点
在何处时,点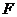 到直线
到直线 的距离最小?
的距离最小?
20.(本小题满分14分)
数列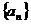 是以
是以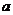 为首项,
为首项, 为公比的等比数列.令
为公比的等比数列.令 ,
,
 ,
,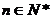 .
.
(1)试用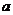 、
、 表示
表示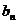 和
和 ;
;
(2)若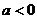 ,
,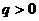 且
且 ,试比较
,试比较 与
与 的大小;
的大小;
(3)是否存在实数对 ,其中
,其中 ,使
,使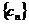 成等比数列.若存在,求出实数对
成等比数列.若存在,求出实数对 和
和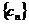 ;若不存在,请说明理由.
;若不存在,请说明理由.
21.(本小题满分14分)
设函数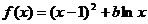 ,其中
,其中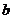 为常数.
为常数.
(1)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(2)若函数 的有极值点,求
的有极值点,求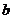 的取值范围及
的取值范围及 的极值点;
的极值点;
(3)求证对任意不小于3的正整数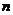 ,不等式
,不等式 都成立.
都成立.
珠海市2008年高三模拟考试
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.D 2.B 3.D 4.A 5.C 6.D 7.C 8.A
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
9. 10.
10. (或
(或 ) 11.
) 11.
12. 13.
13. 14.
14.
15.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
解: ,……………………………………………… 3分
,……………………………………………… 3分
 ,……………………… 3分
,……………………… 3分
(1) ;……………………………………………………. 2分
;……………………………………………………. 2分
(2)因为 的解集为
的解集为 ,
,
所以 为
为 的两根,……………………………………… 2分
的两根,……………………………………… 2分
故 ,所以
,所以 ,
, .……………………………………. 2分
.……………………………………. 2分
17.(本小题满分12分)
解:  ………………………………………… 2分
………………………………………… 2分

 ………………………………………… 2分
………………………………………… 2分
 ……………………………………………………. 2分
……………………………………………………. 2分
(1) 的最大值为
的最大值为 、最小值为
、最小值为 ;……………………………………………… 2分
;……………………………………………… 2分
(2) 单调增,故
单调增,故 ,…………………………… 2分
,…………………………… 2分
即 ,
,
从而 的单调增区间为
的单调增区间为 .…………………… 2分
.…………………… 2分
18.(本小题满分14分)
(1)证明: 底面
底面 ,
,
又 ,
, ,故
,故 面
面
 面
面 ,故
,故 ………………………………………………… 4分
………………………………………………… 4分
(2)证明: ,
, ,故
,故
 是
是 的中点,故
的中点,故
由(1)知 ,从而
,从而 面
面 ,故
,故
易知 ,故
,故 面
面 ……………………………………………… 5分
……………………………………………… 5分
(3)过点 作
作 ,垂足为
,垂足为 ,连结
,连结 .
.
由(2)知, 面
面 ,故
,故 是二面角
是二面角 的一个平面角.
的一个平面角.
设 ,则
,则 ,
, ,
,
从而 ,故
,故 .……………… 5分
.……………… 5分
说明:如学生用向量法解题,则建立坐标系给2分,写出相关点的坐标给2分,第(1)问正确给2分,第(2)问正确给4分,第(3)问正确给4分。
19.(本小题满分14分)
解:(1)抛物线方程为 ……………………………………………………… 2分
……………………………………………………… 2分
故焦点 的坐标为
的坐标为 ………………………………………………………… 2分
………………………………………………………… 2分
(2)设







20.(本小题满分14分)
解:(1)当 时,
时, ,
,

当 时,
时,



所以
 ;…………………… 4分
;…………………… 4分
(2)因为 ,
,
所以

当 时,
时, ,
,
当 时,
时, ,
,
所以当 ,
, 且
且 时,
时, ,即
,即 ;………… 5分
;………… 5分
(3)因为 ,
, ,所以
,所以 ,
,
因为 为等比数列,则
为等比数列,则 或
或 ,
,
所以 或
或 (舍去),所以
(舍去),所以 .………………………… 5分
.………………………… 5分
21.(本小题满分14分)
解:(1)由题意知, 的定义域为
的定义域为 ,
,
 …… 1分
…… 1分
 当
当 时,
时,  ,函数
,函数 在定义域
在定义域 上单调递增. …… 2分
上单调递增. …… 2分
(2)①由(Ⅰ)得,当 时,函数
时,函数 无极值点.
无极值点.
② 时,
时, 有两个相同的解
有两个相同的解 ,
,
 时,
时,
 时,函数
时,函数 在
在 上无极值点.
…… 3分
上无极值点.
…… 3分
③当 时,
时, 有两个不同解,
有两个不同解,


 时,
时, ,
,
 ,
,
此时  ,
, 随
随 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:









减
极小值
增
由此表可知: 时,
时, 有惟一极小值点
有惟一极小值点 ,
…… 5分
,
…… 5分
ii) 当 时,0<
时,0< <1
<1
此时, ,
, 随
随 的变化情况如下表:
的变化情况如下表:













增
极大值
减
极小值
增
由此表可知: 时,
时, 有一个极大值
有一个极大值 和一个极小值点
和一个极小值点 ;
……
7分
;
……
7分
综上所述:
当且仅当 时
时 有极值点;
…… 8分
有极值点;
…… 8分
当 时,
时, 有惟一最小值点
有惟一最小值点 ;
;
当 时,
时, 有一个极大值点
有一个极大值点 和一个极小值点
和一个极小值点
(3)由(2)可知当 时,函数
时,函数 ,
,
此时 有惟一极小值点
有惟一极小值点
且 …… 9分
…… 9分
 …… 11分
…… 11分
令函数
 …… 12分
…… 12分
 …… 14分
…… 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com