
2009年福建省厦门市高三质量检查测试二
数学(理科)试题
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分.
满分为150分,考试时间120分钟.
注意事项:
1. 考生将自己的姓名、准考证号及所有答案均填写在答题卡上;
2. 答题要求,见答题卡上的“填涂样例”和“注意事项”.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A?B)=P(A)?P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率Pn(k)=CnkPk(1-P)n-k
球的表面积公式:S=4πR2,其中R表示球的半径.
球的体积公式:V= πR3,其中R表示球的半径.
πR3,其中R表示球的半径.
第I卷(选择题 共60分)
一、选择题:本大题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在等差数列{an}中,如果a4+a7+a10=15,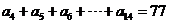 ,
,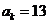 ,那么k等于( )w.w.w.k.s.5.u.c.o.m
,那么k等于( )w.w.w.k.s.5.u.c.o.m
A.14 B.
2 设a>0,b>0,则以下不等式中不恒成立的是 ( )
设a>0,b>0,则以下不等式中不恒成立的是 ( )
A.(a+b)(+)≥4
B.a3+b3≥2ab
3.已知A,B,C,D,E,F,G七个元素排成一排,要求A排在正中间,且B,C相邻,则不同的排法有( )
A.48种 B.96种 C.192种 D.240种
4.设f(x)是定义在R上单调递减的奇函数.若x1+x2>0,x2+x3>0,x3+x1>0,则( )
A.f(x1)+f(x2)+f(x3)<0 B.f(x1)+f(x2)+f(x3)>0
C.f(x1)+f(x2)+f(x3)=0 D.f(x1)+f(x2)>f(x3)
5.已知函数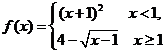 ,则使得f(x)≥1的自变量x的取值范围为( )
,则使得f(x)≥1的自变量x的取值范围为( )
A.(-∞,-2]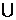 [0,10] B.(-∞,-2]
[0,10] B.(-∞,-2]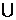 [0,1]
[0,1]
C.(-∞,-2]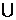 [1,10] D.[-2,0]
[1,10] D.[-2,0]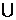 [1,10]
[1,10]
6.在△ABC中,tanA=,cosB=.若最长边为1,则最短边的长为 ( )
A. B. C. D.
7.设 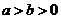 ,那么
,那么 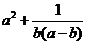 的最小值是( )
的最小值是( )
A.2
B.
8.已知抛物线y2=8x,O是坐标原点,F是焦点,P是抛物线上的点,使得△POF是直角三角形,则这样的P点共有 ( )
A.0个 B.2个 C.4个 D.6个
9.某同学做了10道选择题,每道题四个选择项中有且只有一项是正确的,他每道题都随意地从中选了一个答案.记该同学至少答对9道题的概率为p,则下列数据中与p最接近的是( )
A.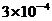 B.
B.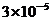 C.
C. D.
D.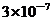
 *10.6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为( )
*10.6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为( )
A.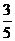 B.
B.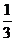 C.
C.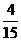 D.
D.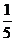
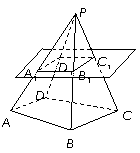
*11.设四棱锥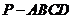 的底面不是平行四边形,用平面
的底面不是平行四边形,用平面 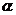 去
去
截此四棱锥,使得截面四边形是平行四边形,则这样的平面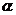 ( )
( )
A.不存在 B.只有1个 C.恰有4个 D.有无数多个
*12.设函数y=f (x)满足f (x+1)=f (x)+1,则方程f (x)=x的根的个数
是 ( )
A.无穷个 B.没有或者有限个 C.有限个 D.没有或者无穷个
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.在答题卡上的相应题目的答题区域内作答.
13. 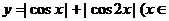 R) 的最小值是
.
R) 的最小值是
.
*14.设集合A={x|log(3-x)≥-2},B={x|≥1},若A∩B=Æ,则实数a的取值范围是_______.
*15.已知函数 ,若
,若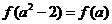 ,则实数a=
.
,则实数a=
.
*16.函数f(x)=xn+(1-x)n,x∈(0,1),n∈N*.记y=f(x)的最小值为an,则a1+a2+…+a6=___.
三、解答题:本大题共6小题,共74分,解答题应写出文字说明,证明过程或演算步骤,在答题卡上相应题目的答题区域内作答.
17.(12分)已知△ABC中,A,B,C的对边分别为a,b,c,且()2=?+?+?.
(Ⅰ)判断△ABC的形状,并求sinA+sinB的取值范围;
*(Ⅱ)若不等式a2(b+c)+b2(c+a)+c2(a+b)≥kabc,对任意的满足题意的a,b,c都成立,求k的取值范围.
18.(12分)一个口袋中装有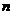 个红球(
个红球( 且
且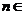 N)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
N)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(Ⅰ)试用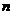 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率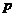 ;
;
(Ⅱ)若 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(Ⅲ) 记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为 .当
.当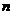 取多少时,
取多少时, 最大?
最大?
19.(12分)定义域均为R的奇函数f(x)与偶函数g(x)满足f(x)+g(x)=10x.
(Ⅰ)求函数f(x)与g(x)的解析式;
(Ⅱ)求函数f(x)的反函数;
(Ⅲ)证明:g(x1)+g(x2)≥
*(Ⅳ)试用f(x1),f(x2),g(x1),g(x2)表示f(x1-x2)与g(x1+x2).
20.(12分)某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100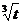 .水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
.水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
21.(12分)设O为坐标原点,A(-,0),点M在定直线x=-p(p>0)上移动,点N在线段MO的延长线上,且满足=.
(Ⅰ)求动点N的轨迹方程,并说明轨迹是什么曲线?
(Ⅱ)若|AN|的最大值≤,求p的取值范围.
22.(14分)已知等差数列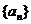 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,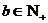 ,且
,且

(Ⅰ)求a的值;
(Ⅱ)若对于任意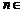 N*,总存在
N*,总存在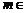 N*,使
N*,使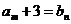 ,求b的值;
,求b的值;
(Ⅲ)甲说:一定存在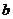 使得
使得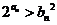 对
对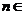 N*恒成立;乙说:一定存在
N*恒成立;乙说:一定存在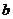 使得
使得 对
对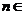 N*恒成立.你认为他们的说法是否正确?为什么?
N*恒成立.你认为他们的说法是否正确?为什么?
2009年厦门市高三质量检查测试二
一、选择题:(本大题12个小题,每小题5分,共60分)
1.B.2.B.3.C.4.A.5.A.6.D.7.C.8.B.9.B.10.C.11.D.12.D.
二、填空题:(本大题4个小题,每小题4分,共16分)
13.; 14.(-∞,-1]∪[3,+∞)∪{0}; 15.1,-1,2,-2; 16.
三、解答题:(本大题6个小题,共74分)
17.(12分)
解:(Ⅰ)∵()2=?+?+?,∴ ()2=?(+)+? ,
即()2=?+?,即?=0.∴△ABC 是以C为直角顶点的直角三角形.
∴sinA+sinB=sinA+cosA=sin(A+),A∈(0,) ,
∴sinA+sinB的取值范围为 .
.
(Ⅱ)在直角△ABC中, a=csinA,b=ccosA.
若a2(b+c)+b2(c+a)+c2(a+b)≥kabc,对任意的满足题意的a、b、c都成立,
则有≥k,对任意的满足题意的a、b、c都成立,
∵
=[c2sin
=[ sin2AcosA+cos
令t=sinA+cosA,t∈ ,
,
设f(t)==t+=t+=t-1++1.
f(t)=t-1++1,当t-1∈ 时
f(t)为单调递减函数,
时
f(t)为单调递减函数,
∴当t=时取得最小值,最小值为2+3,即k≤2+3.
∴k的取值范围为(-∞,2+3].
命题意图:本题是平面向量与三角函数相结合的问题,运用平面向量的运算的意义转化为三角函数的边角关系,进而运用三角函数的图象与性质求值域.第Ⅱ小题将不等式恒成立的问题转化为求三角函数的最值,其中运用了换元法.
18.(12分)
解:(Ⅰ)一次摸奖从 个球中任选两个,有
个球中任选两个,有 种,它们等可能,其中两球不同色有
种,它们等可能,其中两球不同色有 种,一次摸奖中奖的概率
种,一次摸奖中奖的概率 .
.
(Ⅱ)若 ,一次摸奖中奖的概率
,一次摸奖中奖的概率 ,三次摸奖是独立重复试验,三次摸奖(每次摸奖后放回)恰有一次中奖的概率是
,三次摸奖是独立重复试验,三次摸奖(每次摸奖后放回)恰有一次中奖的概率是 .
.
(Ⅲ)设每次摸奖中奖的概率为 ,则三次摸奖(每次摸奖后放回)恰有一次中奖的概率为
,则三次摸奖(每次摸奖后放回)恰有一次中奖的概率为 ,
, ,
,
 ,知在
,知在 上
上 为增函数,在
为增函数,在 上
上 为减函数,当
为减函数,当 时
时 取得最大值.又
取得最大值.又 ,解得
,解得 .
.
答:当 时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大.
时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大.
命题意图:本题是一个在等可能性事件基础上的独立重复试验问题,体现了不同概型的综合.第Ⅲ小题中的函数是三次函数,运用了导数求三次函数的最值.如果学生直接用 代替
代替 ,函数将比较烦琐,这时需要运用换元的方法,将
,函数将比较烦琐,这时需要运用换元的方法,将 看成一个整体,再求最值.
看成一个整体,再求最值.
19.(12分)
(Ⅰ)解:∵f(x)+g(x)=10x ①,∴f(-x)+g(-x)=10-x,∵f(x)为奇函数,g(x)为偶函数,∴f(-x)=-f(x),g(-x)=g(x),∴-f(x)+g(x)=10-x ②,由①,②解得f(x)=(10x-),g(x)=(10x+).
(Ⅱ)由y=(10x-)得,(10x)2-2y×10x-1=0,解得10x=y±,
∵10x>0,∴10x=y+,x=lg(y+),∴f(x)的反函数为f-1(x)=lg(x+).x∈R.
(Ⅲ)解法一:g(x1)+g(x2)=(10+)+(10+)=(10+10)+(+)
≥×2+×2=10+=
解法二:[g(x1)+g(x2)]-
=-=
=≥=0.
(Ⅳ)f(x1-x2)=f(x1)g(x2)-g(x1)f(x2),g(x1+x2)=g(x1)g(x2)-f(x1)f(x2).
命题意图:考查函数的函数解析式,奇函数,单调性,反函数等常规问题的处理方法,第(Ⅲ)问,第(Ⅳ)问把函数与不等式的证明,函数与指对式的化简变形结合起来,考查学生综合应用知识的能力.
20.(12分)
解:设进水量选第x级,则t小时后水塔中水的剩余量为:
y=100+10xt-10t-100 ,且0≤t≤16.
,且0≤t≤16.
根据题意0<y≤300,∴0<100+10xt-10t-100 ≤300.?
≤300.?
当t=0时,结论成立.
当t>0时,由左边得x>1+10( )
)
令m= ,由0<t≤16,m ≥
,由0<t≤16,m ≥ ,
,
记f(t)=1+10( )=1+
)=1+ ),
),
则f¢(t)= .
.
∵当 ≤m <
≤m < 时,f¢(t)>0;当m >
时,f¢(t)>0;当m > 时,f¢(t)<0,
时,f¢(t)<0,
∴所以m = 时(此时t =
时(此时t = ),f(t)最大值=1+10(
),f(t)最大值=1+10( )2-10(
)2-10( )3=
)3= ≈2.48.
≈2.48.
当t= 时,1+10(
时,1+10( )有最大值2.48.∴x>2.48,即x≥3.
)有最大值2.48.∴x>2.48,即x≥3.
由右边得x≤ +1,
+1,
当t=16时, +1有最小值
+1有最小值 +1=
+1= ∈(3,4).即x≤3.
∈(3,4).即x≤3.
21.(12分)
(Ⅰ)解:设N(x0,y0),(x0>0),则直线ON方程为y=x,与直线x=-p交于点M(-p,-),代入=得,=,
或=.
化简得(p2-1)x02+p2y02=p2-1.
把x0,y0换成x,y得点N的轨迹方程为(p2-1)x2+p2y2=p2-1.(x>0)
(1)当0<p<1时,方程化为x2-=1表示焦点在x轴上的双曲线的右支;
(2)当p=1时,方程化为y=0,表示一条射线(不含端点);
(3)当p>1时,方程化为x2+=1表示焦点在x轴上的椭圆的右半部分.
(Ⅱ)解:由(Ⅰ)可知|AN|==
==x0+1.
当0<p<1时,因x0∈[1,+∞),故|AN|无最大值,不合题意.
当p=1,因x0∈(0,+∞),故|AN|无最大值,不合题意.
当p>1时,x0∈(0,1],故当x0=1时,|AN|有最大值+1,由题意得+1≤,
解得p≥2.所以p的取值范围为[2,+∞).
命题意图:通过用设点,代换,化简,检验等步骤求曲线方程,考查解析几何中已知曲线求方程的能力,并结合含参数的方程表示的曲线类型的讨论考查学生的分类讨论思想的应用.
22.(14分)
解:(Ⅰ)∵  ,a,
,a, N*,
N*,
∴  ∴
∴  ∴
∴ 
∴ 
 ∴ a=2或a=3.
∴ a=2或a=3.
∵当a=3时,由 得
得 ,即
,即 ,与
,与 矛盾,故a=3不合题意.
矛盾,故a=3不合题意.
∴a=3舍去, ∴a=2.
(Ⅱ) ,
, ,由
,由 可得
可得 .
.
∴ .∴
.∴
 是5的约数,又
是5的约数,又 ,∴ b=5 .
,∴ b=5 .
(Ⅲ)若甲正确,则存在 (
( )使
)使 ,即
,即 对
对 N*恒成立,
N*恒成立,
当 时,
时, ,无解,所以甲所说不正确.
,无解,所以甲所说不正确.
若乙正确,则存在 (
( )使
)使 ,即
,即 对
对 N*恒成立,
N*恒成立,
当 时,
时, ,只有在
,只有在 时成立,
时成立,
而当 时
时 不成立,所以乙所说也不成立.
不成立,所以乙所说也不成立.
命题意图:本题首先考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,用两边夹的方法确定整数参数.第Ⅲ小题对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com