
吉林长春三中2008-2009学年度高三第一次模拟考试数学理科 2008.09
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
注意事项:
1.答题前,考生务必将姓名和准考证号填写在每一页答题纸上的指定位置;
2.将每科答案按照要求填写在答题卡指定位置,填写在试题卷上无效;
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共计60分)
1.设集合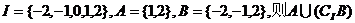 = ( )
= ( )
A.{1} B.{1,2} C.{2} D.{0,1,2}
2.计算: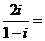 ( )
( )
A.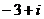 B.
B. 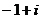 C.
C.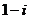 D.
D. 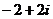
3.若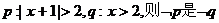 成立的 ( )
成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.函数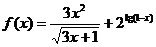 的定义域是 ( )
的定义域是 ( )
A.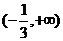 B.
B.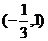 C.
C.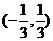 D.
D.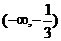
5.函数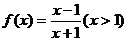 的反函数为 ( )
的反函数为 ( )
A.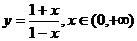 B.
B.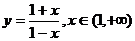
C.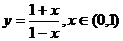 D.
D.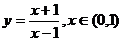
6.已知a=(1,2),b=(3,-1)且a + b与a-λb互相垂直,则实数的λ值为 ( )
A.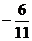 B.
B.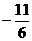 C.
C. D.
D.
7.过点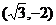 的直线l经过圆
的直线l经过圆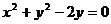 的圆心,则直线l的倾斜角大小为( )
的圆心,则直线l的倾斜角大小为( )
A.150° B.120° C.30° D.60°
8.在△ABC中,已知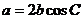 ,那么这个三角形一定是 ( )
,那么这个三角形一定是 ( )
A.等边三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形
9.如果函数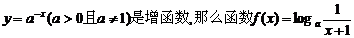 的图象大致是( )
的图象大致是( )
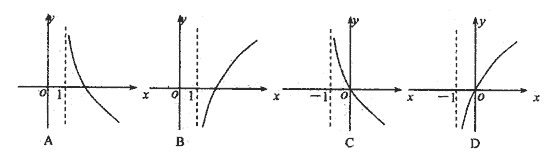
|