|
Ⅰ Ⅱ Ⅲ Ⅳ sin cos tan cot ⑹两个特殊的公式: 如果 ∈ ∈ ,那么sin ,那么sin < < < <  推论: 推论: >0则sin >0则sin < < 如果 ∈ ∈ ,那么1<sin ,那么1<sin +cos +cos ≤ ≤ 一、知识点训练:
试题详情
试题详情
试题详情
4、在-720º到720º之间与-1050º终边相同的角是
. 试题详情
5、sin2?cos3?tan4的符号是………………………………………………………………………( ) (A)小于0
(B)大于0
(C)等于0
(D)不确定 试题详情
试题详情
试题详情
二、典型例题分析: 1、确定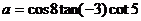 的符号 的符号 试题详情
试题详情
3、如果角 的终边在直线y=3x上,求cos 的终边在直线y=3x上,求cos 与tan 与tan 的值. 的值. 试题详情
4、扇形的周长为20cm,问其半径为多少时其面积最大? 试题详情
三、课堂练习: 1、角 终边上有一点(a,a)则sin 终边上有一点(a,a)则sin =…………………………………………………………( ) =…………………………………………………………( ) 试题详情
试题详情
2、如果 是第二象限角,那么- 是第二象限角,那么-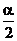 是第……………………………………………( )象限角 是第……………………………………………( )象限角 (A)Ⅱ或Ⅲ
(B) Ⅰ或Ⅱ
(C) Ⅰ或Ⅲ (D) Ⅱ或Ⅳ 试题详情
试题详情
试题详情
试题详情
四、课堂小结: 1、要熟悉任意角的概念,掌握角度与弧度的转化方法,熟练掌握任意角三角函数的定义方法. 试题详情
2、已知角的一个三角函数值求其它三角函数值时,必须对讨论角的范围 试题详情
3、知道 所在的象限能熟练求出 所在的象限能熟练求出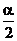 所在象限. 所在象限. 五、能力测试:
姓名
得分 试题详情
1、下列结果为正值的是……………………………………………………………………………( )
(A)cos2-sin2
(B)tan3?sec2 (C)cos2?sin2 (D) sin2?tan2 试题详情
*2、已知锐角 终边上有一点(2sin3,-2cos3),那么 终边上有一点(2sin3,-2cos3),那么 =………………………………………( ) =………………………………………( ) 试题详情
(A)3 (B)-3
(C)3- (D)
(D)  -3 -3 试题详情
试题详情
试题详情
4、2弧度的圆心角所对的弦长为2,那么此圆心角所夹扇形的面积的数值为…………………( ) 试题详情
试题详情
5、如果角 是第二象限角,那么角 是第二象限角,那么角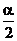 是第
象限角. 是第
象限角. 同角三角函数关系与诱导公式 〖考纲要求〗掌握同角三角函数关系和诱导公式,能运用上述公式化简三角函数式、求任意角的三角函数值与证明较简单的三角恒等式. 〖复习要求〗掌握并熟练应用同角三角函数关系和诱导公式. 〖复习建议〗重点从同角三角函数关系和诱导公式出发,解决知值求值的一些题型. 试题详情
6、已知第二、第三象限角x满足cosx= ,求实数a的取值范围. ,求实数a的取值范围.
试题详情
sin( + + )=
;sin( )=
;sin( - -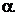 )= ; )= ;
⑵同角三角函数关系: 平方关系:
倒数关系: 商的关系: 试题详情
一、知识点训练: 1、sin( - - )=……………………………………………………………………………………( ) )=……………………………………………………………………………………( ) 试题详情
试题详情
3、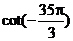 =……………………………………………………………………………………( ) =……………………………………………………………………………………( ) 试题详情
试题详情
4、设A、B、C是ㄓABC的三个内角,则下列四个表达式⑴cos(A+B)+cosC;⑵sin(A+B)+sinC;⑶ ;⑷ ;⑷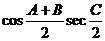 ,始终表示常数的是………………………………( ) ,始终表示常数的是………………………………( ) (A)⑴
(B) ⑴⑶
(C) ⑵⑷
(D)⑶⑷ 试题详情
二、典型例题分析:
1、求值: sin(-660º)cos420º-tan330ºcot(-690º)
试题详情
试题详情
3、已知 ,求 ,求 之值. 之值. 试题详情
4、已知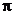 < < <2 <2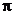 ,cos( ,cos( -9 -9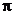 )=- )=- ,求cot( ,求cot( - -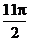 ) ) 试题详情
试题详情
三、课堂练习:
试题详情
试题详情
试题详情
(A) (B)1
(C) 2 (D)4 (B)1
(C) 2 (D)4 试题详情
3、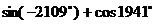 =……………………………………………………………………( ) =……………………………………………………………………( ) (A)0 (B)2sin51º (C) 2cos51º (D)
-2sin51º 试题详情
4、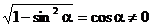 ,那么 ,那么 是第
象限的角. 是第
象限的角. 试题详情
四、课堂小结: 1、记忆诱导公式方法:“奇变偶不变(横同竖余)、符号看象限”. 试题详情
2、角的运算规则:“偶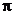 丢,奇 丢,奇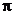 留”,“负化正,大化小、化到锐角再查表” 留”,“负化正,大化小、化到锐角再查表” 试题详情
3、用同角三角函数关系时,首先考虑平方关系,但是要注意符号的讨论. 五、能力测试:
姓名
得分 试题详情
试题详情
试题详情
2、sin600º的值为………………………………………………………………………………………( ) 试题详情
试题详情
3、锐角 能使下列等式成立的是………………………………………………………………( ) 能使下列等式成立的是………………………………………………………………( ) 试题详情
试题详情
4、cot10º+cot190º+tan100º+cot350º+sin1590ºcos(-1860º)+cot(-960º)cot1395º= . 试题详情
试题详情
6、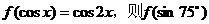 =
. =
. 试题详情
7、化简: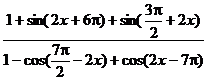 试题详情
8、如果 ,求sinx之值. ,求sinx之值. 角的和、差、倍 〖考纲要求〗能推导两角和、差、倍、半的正弦、余弦、正切公式. 〖复习建议〗在复习中要注意掌握三角变形的方法和技巧:1的替换、角的变换(拼凑、分拆)、降次与升次,了解万能代换 〖知识回顾〗 试题详情
两角和差公式: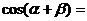 .
倍角公式:sin2 .
倍角公式:sin2 =
. =
. 试题详情
 .
cos2
.
cos2 = . = .
试题详情
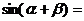 . .
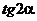 =
. =
. 试题详情
 .
.
试题详情
一、知识点训练: 1、sin(x-y)cosy+cos(x-y)siny=
. 试题详情
2、tgx=2,那么sin2x=
;cos2x=
;tg2x=
;tg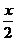 =
. =
. 试题详情
3、如果 ,则tg ,则tg =………………………………………………………( ) =………………………………………………………( ) 试题详情
试题详情
二、典型例题分析: 1、求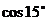 之值. 之值. 试题详情
试题详情
3、在△ABC中,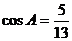 , , ,求sinC的值. ,求sinC的值. 试题详情
试题详情
5、设tan ,tan ,tan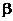 是一元二次方程:ax2+bx+c=0(abc≠0)的两个实数根,求 是一元二次方程:ax2+bx+c=0(abc≠0)的两个实数根,求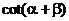 的值. 的值. 试题详情
三、课堂练习: 1、利用公式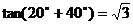 求:tan20º+tan40º+ 求:tan20º+tan40º+ tan20ºtan40º=
. tan20ºtan40º=
. 试题详情
2、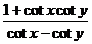 =…………………………………………………………………………………( ) =…………………………………………………………………………………( ) (A) tan(x-y)
(B)-tan(x-y) (C)cot(x-y) (D)-cot(x-y) 试题详情
3、如果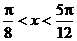 ,则函数 ,则函数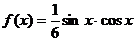 的值域为…………………………………( ) 的值域为…………………………………( ) 试题详情
试题详情
4、 ………………………………………………………( ) ………………………………………………………( ) 试题详情
(A) (B)- (B)- (C) (C)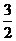 (D)- (D)-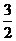 处理三角函数的和、差、倍、半问题,一个最重要的内容是能熟练记住几组公式:两角和与差的三角函数、倍角与半角公式,最好能记住万能公式,要学会根据角的范围确定三角函数的符号,掌握几种公式的变形结果并且能熟练使用. 五、能力测试:
姓名
得分 试题详情
四、课堂小结:
试题详情
试题详情
2、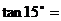 …………………………………………………………………………………………( ) …………………………………………………………………………………………( ) 试题详情
试题详情
3、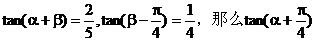 =…………………………………………( ) =…………………………………………( ) 试题详情
试题详情
4、tan18º+tan42º+ tan18ºtan42º=
.
5、 tan18ºtan42º=
.
5、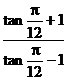 =
. =
. 试题详情
试题详情
7、在等腰三角形ABC中,B=C, ,求sinB. ,求sinB. 试题详情
8、已知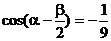 , ,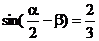 ,并且 ,并且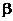 ∈(0, ∈(0, ), ), ∈( ∈( , ,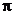 ),求 ),求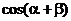 . . 三角函数式的化简 求值 证明 〖考纲要求〗能运用三角函数公式化简三角函数式、在化简的基础上会求某些三角函数式的值,会证明比较简单的三角恒等式(包括条件恒等式). 试题详情
〖复习建议〗1、在复习中主要熟练公式的各种变形;掌握化简的常用方法:异角化同角、异次化同次、高次化低次、切割化弦、特殊值与特殊角的转化;掌握化简的基本要求:项数尽可能要少、次数尽可能的低、函数种类尽可能的少、能求值的尽量求值;在处理化简问题时,观察表达式的结构特点和问题中出现的角的关系尤为重要. 试题详情
2、在复习中主要熟练公式的各种变形,注意公式的逆向使用、变形使用.掌握恒等变形的基本方法:异角化同角、高次化低次、特殊值与特殊角的转换、条件的代入等.在做题过程中,要注意做到:过程详细,不能遗漏任何一个知识点. 〖知识回顾〗 试题详情
一、知识点训练: 1、如果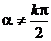 ,那么 ,那么 的值…………………………………………………( ) 的值…………………………………………………( ) (A)大于0 (B)不小于0 (C)小于0 (D) 符号不定 试题详情
2、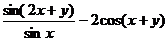 等于………………………………………………………………( ) 等于………………………………………………………………( ) 试题详情
试题详情
3、sinx?cosx=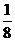 , ,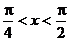 ,则cosx-sinx=
. ,则cosx-sinx=
. 试题详情
4、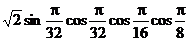 = . = . 试题详情
5、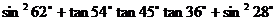 =
. =
. 试题详情
二、典型例题分析: 1、化简表达式: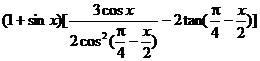 试题详情
2、化简表达式: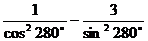 试题详情
3、如果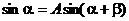 ,求证: ,求证: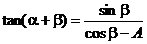 . . 试题详情
试题详情
5、求值: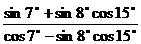 试题详情
试题详情
试题详情
三、课堂练习: 1、化简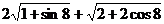 的最简式为…………………………………………………( ) 的最简式为…………………………………………………( ) (A) 2sin4 (B)2sin4-4cos4 (C)-2sin4-4cos4 (D)4cos4-2sin4 试题详情
2、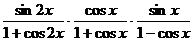 的最简形式为
. 的最简形式为
. 试题详情
3、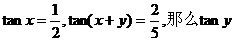 = . = . 五、能力测试:
姓名
得分 . 试题详情
1、如果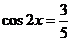 ,那么sin4x+cos4x=…………………………………………………………( ) ,那么sin4x+cos4x=…………………………………………………………( ) 试题详情
试题详情
2、如果 ,则 ,则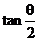 =…………………………………………………………( ) =…………………………………………………………( ) 试题详情
(A)2
(B) (C) (C)  或者不存在 (D) 不存在 或者不存在 (D) 不存在 试题详情
3、(2003广东考题)x∈(- ,0), ,0),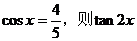 =……………………………………( ) =……………………………………( ) 试题详情
试题详情
4、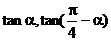 是方程:x2+px+q=0的两个根,那么……………………………………( ) 是方程:x2+px+q=0的两个根,那么……………………………………( )
(A)p-q+1=0 (B)p+q+1=0 (C)p+q-1=0 (D)
p-q-1=0 试题详情
5、sinx+sin2x=1,则cos2x+cos4x=
. 试题详情
试题详情
〖考纲要求〗了解正弦、余弦、正切、余切函数图象的画法,会用“五点法”画正弦、余弦以及函数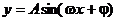 的图象,并能解决与正弦曲线有关的实际问题. 的图象,并能解决与正弦曲线有关的实际问题. 试题详情
〖复习建议〗熟练掌握三角函数特别是正弦、余弦函数的图象,深刻理解并且熟练掌握函数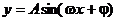 中参量A、 中参量A、 、 、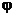 对正弦函数y=sinx图象的影响;用“五点法”画图象时,关键是正确选取“五点”,在如何选择“五点”上下工夫. 对正弦函数y=sinx图象的影响;用“五点法”画图象时,关键是正确选取“五点”,在如何选择“五点”上下工夫. 〖知识回顾〗函数图象的几种常见变换: 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
5、 。
。 试题详情
一、知识点训练: 1、把函数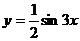 的图象向左平移 的图象向左平移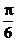 个单位,得到函数的解析式为……………………( ) 个单位,得到函数的解析式为……………………( ) 试题详情
试题详情
2、要得到函数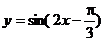 的图象,只要将函数 的图象,只要将函数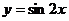 的图象……………………( ) 的图象……………………( ) 试题详情
试题详情
试题详情
二、典型例题分析:
试题详情
2、如果函数y=msin2x-cos2x的图象关于直线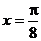 对称,同时关于点(a,b)对称,求实数m以及a、b应该满足的条件. 对称,同时关于点(a,b)对称,求实数m以及a、b应该满足的条件. 试题详情
3、已知函数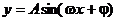 的图形的一个最高点为(2, 的图形的一个最高点为(2, ),由这个最高点到相邻的最低点时曲线经过(6,0),求这个函数的一个解析式. ),由这个最高点到相邻的最低点时曲线经过(6,0),求这个函数的一个解析式. 试题详情
*4、方程:sinx+cosx+m=0在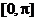 上有两个不等的实数根 上有两个不等的实数根 、 、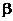 ,求实数m的取值范围以及 ,求实数m的取值范围以及 + +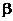 的值. 的值. 试题详情
三、课堂练习: 1、要得到函数y=cosx的图象,至少要把函数y=sinx的图象向左平移
个单位. 试题详情
2、函数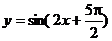 的图象的一条对称轴为……………………………………………( ) 的图象的一条对称轴为……………………………………………( ) 试题详情
试题详情
试题详情
4、函数y=2cosx的图象与直线y=2在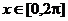 时围成的图象面积为
. 时围成的图象面积为
. 三角函数的图象问题有一定的综合性,含有:周期性、奇偶性、最值、函数变换等内容,问题小,但是考察的方法灵活,学习方法包括:观察法、特殊结论法、函数变换法,要多加练习. 五、能力测试:
姓名
得分 试题详情
四、课堂小结:
试题详情
试题详情
试题详情
 2、函数y=cos(2x+ 2、函数y=cos(2x+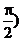 的图象的一条对称轴方程是………………( ) 的图象的一条对称轴方程是………………( )
试题详情
试题详情
3、如果右图是周期是2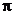 的三角函数的图象,则其表达式是……( ) 的三角函数的图象,则其表达式是……( ) (A)sin(1+x) (B)sin(-1-x) (C)sin(x-1) (D)sin(x-1) 试题详情
4、要得到函数y=cos(2x-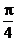 )的图象,只要将函数y=sin2x的图象………………………………( ) )的图象,只要将函数y=sin2x的图象………………………………( ) 试题详情
试题详情
试题详情
(A)y=sin2x
(B)y=-sin2x (C) (D) (D) 试题详情
6、要得到函数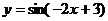 的图象,只要把函数 的图象,只要把函数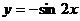 的图象向 平移 个单位. 的图象向 平移 个单位. 试题详情
7、如果图象x2+y2≤k2至少覆盖函数 的一个最大值点和一个最小值点,则正整数k 的最小值为
. 的一个最大值点和一个最小值点,则正整数k 的最小值为
. 试题详情
8、已知函数y= cos2x+ cos2x+ sinx?cosx,x∈R, sinx?cosx,x∈R, ①当函数y取得最大值时,求自变量x的集合 ②该函数的图象可以由y=sinx,x∈R的图象经过怎样的平移和伸缩得到? 三角函数的性质(1) 试题详情
〖考纲要求〗掌握三角函数的性质,了解周期函数和最小正周期的意义,会求形如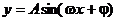 的函数和可以转化为此类函数的最小正周期. 的函数和可以转化为此类函数的最小正周期. 试题详情
〖复习建议〗牢记三角函数y=sinx、y=cosx的基本特征,包括定义域、值域、最小正周期等,会求函数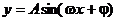 的最小正周期. 的最小正周期. 〖知识回顾〗请填写下列表格: 函数 定义域 值域 周期性 y=sinx y=cosx [-1,1] y=tanx 试题详情
周期为T=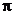 y=cotx 试题详情
{x|x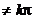 ,x∈R,k∈Z} ,x∈R,k∈Z} 试题详情
试题详情

注意:求函数的最小正周期时,一定要把函数表达式转化为最简形式,然后利用公式处理. 试题详情
一、知识点训练: 1、如果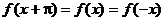 ,那么此函数是……………………………………………( ) ,那么此函数是……………………………………………( ) (A)|sinx| (B)cosx (C)sin2x
(D)tanx 试题详情
2、下列表示同一函数的是…………………………………………………………………………( ) 试题详情
试题详情
试题详情
3、函数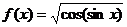 的定义域为
. 的定义域为
. 试题详情
4、已知sin(30º+120º)=sin30º,那么30º是y=sinx的周期,对吗?
. 试题详情
二、典型例题分析: 1、求函数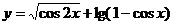 的定义域. 的定义域. 试题详情
试题详情
⑴y=sin(-2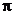 x+4) ;⑵y=sin4x-cos4x . x+4) ;⑵y=sin4x-cos4x . 试题详情
⑶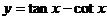 ;⑷y=2sin2x-
;⑷y=2sin2x- sinx?cosx+5
. sinx?cosx+5
. 试题详情
3、函数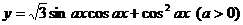 的周期为 的周期为 . . 试题详情
⑴求实数a之值;⑵当0≤x≤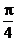 时,求此函数的最值及此时的x之值. 时,求此函数的最值及此时的x之值. 试题详情
三、课堂练习: 1、函数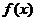 的定义域为[0,1],那么函数 的定义域为[0,1],那么函数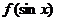 的定义域为
. 的定义域为
. 试题详情
2、函数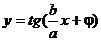 的最小正周期为………………………………………………………( ) 的最小正周期为………………………………………………………( ) 试题详情
试题详情
3、关于函数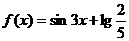 的周期问题,正确的是………………………………………( ) 的周期问题,正确的是………………………………………( ) 试题详情
(A)不是周期函数 (B)T=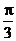 (C) (C)
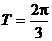 (D)
6 (D)
6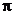 三角函数的定义域与三角函数线有密切关系,要对正弦与余弦以及正切函数线非常熟悉,同时要记住一些特殊的三角函数值;三角函数的周期性是此部分的重要内容,要掌握基本三角函数周期并且会求一些特殊的三角函数周期. 五、能力测试:
姓名
得分 试题详情
四、课堂小结: 1、函数cot 的最小正周期为………………………………………………………………………( ) 的最小正周期为………………………………………………………………………( ) 试题详情
试题详情
2、函数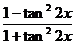 的最小正周期为………………………………………………………………( ) 的最小正周期为………………………………………………………………( ) 试题详情
试题详情
3、满足sin(x-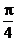 )≥ )≥ 的x的集合是………………………………………………………………( ) 的x的集合是………………………………………………………………( ) 试题详情
试题详情
试题详情
4、在区间(0,2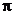 )内,使sinx>cosx成立的x的取值范围是……………………………………( ) )内,使sinx>cosx成立的x的取值范围是……………………………………( ) 试题详情
试题详情
5、函数y=sin(2+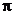 x)的最小正周期为 x)的最小正周期为
试题详情
6、函数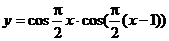 的最小正周期为
. 的最小正周期为
. 三角函数的性质(2) 〖考纲要求〗掌握三角函数的性质. 〖考试内容〗正弦、余弦、正切、余切函数的性质. 〖复习建议〗在熟练掌握基本三角函数性质的基础上,要善于把三角函数式尽可能转化为只含一个三角函数的“标准式”,进而取确定其性质,在确定三角函数的单调区间时,常可先分析函数的定义域和周期,画出大致图象后在通过观察得出结论. 〖知识回顾〗 函数 奇偶性 单调区间 y=sinx 增区间: 减区间: |
