
北京市2009届高三第二次模拟考试
数学文科
(试卷总分150分 考试时间120分钟)
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是最符合题目要求的.)
1. 的值是( )
的值是( )
A.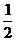 B.
B.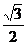 C.
C. 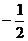 D.
D. 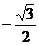
2.某大学有学生1500人,其中汉族学生1200人,回族学生250人,藏族学生50人,学校食堂为了解学生的就餐情况,现抽取容量是150的样本,则抽取回族学生人数是( )
A.15
B.
3.已知集合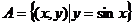 ,集合
,集合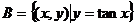 ,则
,则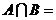 ( )
( )
A. 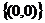 B.
B. 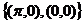 C.
C.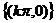 D.
D. 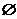
4.设向量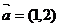 ,
,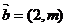 ,若
,若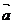 ∥
∥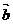 ,则
,则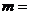 ( )
( )
A.-1
B.
5.已知正项等差数列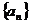 的前6项和为9,
的前6项和为9,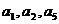 成等比数列,则数列
成等比数列,则数列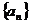 的公差为( )
的公差为( )
A. 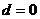 B.
B.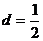 C.
C.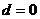 或
或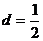 D.
D. 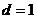 或
或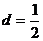
6.若双曲线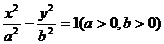 的右焦点到一条渐近线的距离等于焦距的
的右焦点到一条渐近线的距离等于焦距的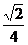 ,则此双曲线的渐近线方程是( )
,则此双曲线的渐近线方程是( )
A.
y=x+3
B. y=x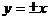
7.设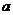 、
、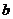 为正实数,则下列不等式恒成立的是( )
为正实数,则下列不等式恒成立的是( )
① ;②
;②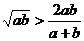 ;③
;③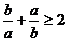 ;④
;④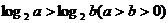 。
。
A. ①③ B. ②③④ C. ①③④ D. ①②③
8.设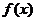 是
是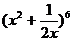 展开式的中间项,若
展开式的中间项,若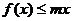 在区间
在区间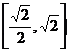 上恒成立,则实数
上恒成立,则实数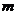 的取值范围是( )
的取值范围是( )
A.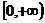 B.
B.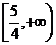 C.
C. 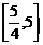 D.
D.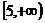
9.函数 的最小正周期是( )
的最小正周期是( )
A.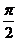 B.
B.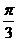 C.
C. 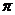 D.
D.
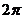
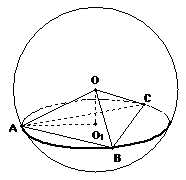
10.用平面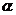 截半径为
截半径为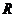 的球
的球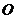 ,若截面圆的内接正三角形
,若截面圆的内接正三角形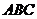 的边长亦为
的边长亦为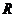 ,则三棱锥
,则三棱锥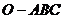 的体积为(
)
的体积为(
)
A.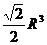 B.
B.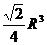 C.
C. D.
D.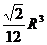
 11.设
11.设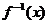 是函数
是函数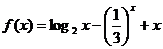
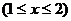 的反函数,则
的反函数,则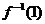 与
与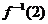 的大小关系为( )
的大小关系为( )
A. 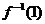
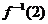 B.
B.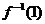

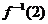
C.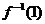
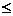
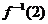 D
D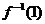
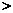
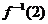
12.直线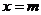 ,
,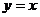 将圆面
将圆面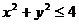 分成若干块,现用5种颜色给这若干块涂色,每块只涂一种颜色,且任意两块不同色,共有120种涂法,则m的取值范围是 ( )
分成若干块,现用5种颜色给这若干块涂色,每块只涂一种颜色,且任意两块不同色,共有120种涂法,则m的取值范围是 ( )
A.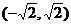 B.
B.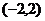
C.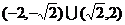 D.
D.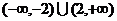
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分,把正确的答案填在指定位置上)
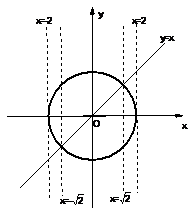 13. “
13. “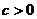 ”是“
”是“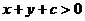 表示直线
表示直线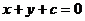 右侧区域”的 条件。
右侧区域”的 条件。
 14.已知数列
14.已知数列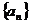 的前
的前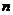 项和
项和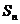 比集合
比集合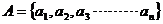 的子集个数少1,则数列
的子集个数少1,则数列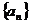 通项公式是
。
通项公式是
。
15.如图,正四面体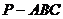 中,
中,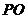 是底面
是底面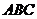 上的高,
上的高,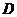 为
为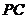 的中点,则
的中点,则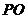 与
与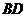 所成角的余弦值为
。
所成角的余弦值为
。
16,已知点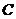 为
为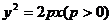 的准线与
的准线与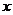 轴的交点,点
轴的交点,点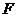 为焦点,点
为焦点,点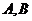 为抛物线上两个点,若
为抛物线上两个点,若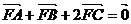 ,则向量
,则向量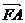 与
与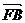 的夹角为
。
的夹角为
。
三.解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
已知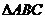 的内角
的内角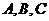 的对边分别为
的对边分别为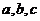 ,其中
,其中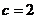 ,
,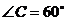 ,
,
(Ⅰ)若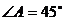 ,求
,求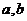 的值;
的值;
(Ⅱ)若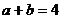 ,求
,求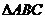 的面积。
的面积。
18. (本小题满分12分)
高中会考成绩分A,B,C,D四个等级,其中等级D为会考不合格,某学校高三学生甲参加语文、数学、英语三科会考,三科会考合格的概率均为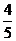 ,每科得A,B,C,D 四个等级的概率分别为
,每科得A,B,C,D 四个等级的概率分别为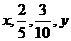 ,
,
(Ⅰ)求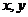 的值;
的值;
(Ⅱ)若有一科不合格,则不能拿到高中毕业证,求学生甲不能拿到高中毕业证的概率;
(Ⅲ)若至少有两科得A,一科得B,就能被评为三好学生,则学生甲被评为三好学生的概率;
19.(本小题满分12分)
已知数列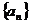 的前
的前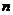 项和为
项和为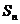 ,且
,且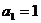 ,
,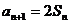 ,
,
(Ⅰ)求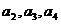 的值;
的值;
(Ⅱ)求数列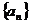 的通项公式
的通项公式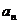 ;
;
(Ⅲ)设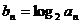 ,求数列
,求数列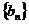 的前
的前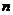 项和
项和 。
。
20.(本小题满分12分)
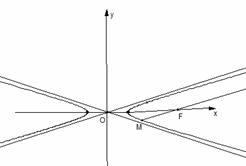 已知四棱锥
已知四棱锥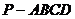 的底面
的底面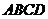 为直角梯形,
为直角梯形,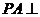 底面
底面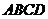 ,
,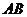 ∥
∥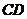 ,
,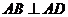 ,
,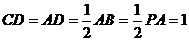 ,点
,点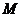 、
、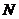 分别在棱
分别在棱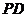 、
、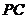 上,且
上,且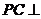 平面
平面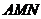 ,
,
(Ⅰ)求证: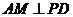 ;
;
(Ⅱ)求二面角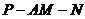 的正切值的大小;
的正切值的大小;
(Ⅲ)求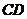 与平面
与平面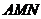 所成角正切值的大小。
所成角正切值的大小。
21.(本小题满分12分)
已知抛物线 与椭圆
与椭圆 都经过点
都经过点 ,它们在
,它们在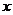 轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点。
轴上有共同焦点,椭圆的对称轴是坐标轴,抛物线的顶点为坐标原点。
(Ⅰ)求抛物线与椭圆的方程;
(Ⅱ)已知动直线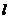 过点
过点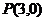 ,交抛物线
,交抛物线 于
于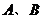 两点,是否存在垂直于
两点,是否存在垂直于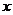 轴的直线
轴的直线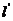 被以
被以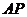 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出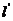 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
22.(本小题满分12分)
已知函数 的导函数是偶函数,
的导函数是偶函数,
(Ⅰ)若 ,求函数
,求函数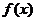 的极值;
的极值;
(Ⅱ)设函数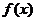 在点
在点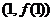 处的切线斜率为
处的切线斜率为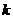 ,若
,若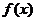 在区间
在区间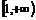 上为增函数,求
上为增函数,求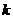 的取值范围。
的取值范围。
1.解析: ,故选A。
,故选A。
2.解析:抽取回族学生人数是 ,故选B。
,故选B。
3.解析:由 ,得
,得 ,此时
,此时 ,所以,
,所以, ,故选C。
,故选C。
4.解析:∵ ∥
∥ ,∴
,∴ ,∴
,∴ ,故选C。
,故选C。
5.解析:设公差为 ,由题意得,
,由题意得, ;
; ,解得
,解得 或
或 ,故选C。
,故选C。
6.解析:∵双曲线 的右焦点到一条渐近线的距离等于焦距的
的右焦点到一条渐近线的距离等于焦距的 ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴双曲线的渐近线方程是
,∴双曲线的渐近线方程是 ,故选D.
,故选D.
7.解析:∵ 、
、 为正实数,∴
为正实数,∴ ,∴
,∴ ;由均值不等式得
;由均值不等式得 恒成立,
恒成立, ,故②不恒成立,又因为函数
,故②不恒成立,又因为函数 在
在 是增函数,∴
是增函数,∴ ,故恒成立的不等式是①③④。故选C.
,故恒成立的不等式是①③④。故选C.
8.解析:∵ ,∴
,∴ 在区间
在区间 上恒成立,即
上恒成立,即 在区间
在区间 上恒成立,∴
上恒成立,∴ ,故选D。
,故选D。
9.解析:∵

 ,∴此函数的最小正周期是
,∴此函数的最小正周期是 ,故选C。
,故选C。
10.解析:如图,∵正三角形 的边长为
的边长为 ,∴
,∴ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,故选D。
,故选D。
11.解析:∵ 在区间
在区间 上是增函数且
上是增函数且 ,∴其反函数
,∴其反函数 在区间上
在区间上 是增函数,∴
是增函数,∴

 ,故选A
,故选A
12.解析:如图,①当 或
或 时,圆面
时,圆面 被分成2块,涂色方法有20种;②当
被分成2块,涂色方法有20种;②当 或
或 时,圆面
时,圆面 被分成3块,涂色方法有60种;
被分成3块,涂色方法有60种;
③当 时,圆面
时,圆面 被分成4块,涂色方法有120种,所以m的取值范围是
被分成4块,涂色方法有120种,所以m的取值范围是 ,故选A。
,故选A。
13.解析:将 代入
代入 结果为
结果为 ,∴
,∴ 时,
时, 表示直线
表示直线 右侧区域,反之,若
右侧区域,反之,若 表示直线
表示直线 右侧区域,则
右侧区域,则 ,∴是充分不必要条件。
,∴是充分不必要条件。
 14.解析:∵
14.解析:∵ ,∴
,∴ 时,
时, ,又
,又 时,
时, 满足上式,因此,
满足上式,因此, 。
。
 15.解析:设正四面体的棱长为
15.解析:设正四面体的棱长为 ,连
,连 ,取
,取 的中点
的中点 ,连
,连 ,∵
,∵ 为
为 的中点,∴
的中点,∴ ∥
∥ ,∴
,∴ 或其补角为
或其补角为 与
与 所成角,∵
所成角,∵ ,
, ,∴
,∴ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴
,∴ 与
与 所成角的余弦值为
所成角的余弦值为 。
。
 16.解析:∵
16.解析:∵ ,∴
,∴ ,∵点
,∵点 为
为 的准线与
的准线与 轴的交点,由向量的加法法则及抛物线的对称性可知,点
轴的交点,由向量的加法法则及抛物线的对称性可知,点 为抛物线上关于轴对称的两点且做出图形如右图,其中
为抛物线上关于轴对称的两点且做出图形如右图,其中 为点
为点 到准线的距离,四边形
到准线的距离,四边形 为菱形,∴
为菱形,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴向量
,∴向量 与
与 的夹角为
的夹角为 。
。
17.(10分)解析:(Ⅰ)由正弦定理得, ,
, ,…2分
,…2分
∴ ,
, ,………4分
,………4分
(Ⅱ)∵ ,
, ,∴
,∴ ,∴
,∴ ,………………………6分
,………………………6分
又∵ ,∴
,∴ ,∴
,∴ ,………………………8分
,………………………8分
∴ 。………………………10分
。………………………10分
18.解析:(Ⅰ)∵ ,∴
,∴ ;……………………理3文4分
;……………………理3文4分
(Ⅱ)∵三科会考不合格的概率均为 ,∴学生甲不能拿到高中毕业证的概率
,∴学生甲不能拿到高中毕业证的概率 ;……………………理6文8分
;……………………理6文8分
(Ⅲ)∵每科得A,B的概率分别为 ,∴学生甲被评为三好学生的概率为
,∴学生甲被评为三好学生的概率为 。……………………12分
。……………………12分
19.(12分)解析:(Ⅰ)∵ ,∴
,∴ ,
,
 ,
, ,……………3分
,……………3分
(Ⅱ)∵ ,∴
,∴
 ,
,
∴ ,
,

又 ,∴数列
,∴数列 自第2项起是公比为
自第2项起是公比为 的等比数列,………………………6分
的等比数列,………………………6分
∴ ,………………………8分
,………………………8分
(Ⅲ)∵ ,∴
,∴ ,………………10分
,………………10分
∴ 。………………………12分
。………………………12分
20.解析:(Ⅰ)∵ ∥
∥ ,
, ,∴
,∴ ,∵
,∵ 底面
底面 ,∴
,∴ ,∴
,∴ 平面
平面 ,∴
,∴ ,又∵
,又∵ 平面
平面 ,∴
,∴ ,∴
,∴ 平面
平面 ,∴
,∴ 。………………………4分
。………………………4分
(Ⅱ)∵ 平面
平面 ,∴
,∴ ,
, ,∴
,∴ 为二面角
为二面角 的平面角,………………………6分
的平面角,………………………6分
 ,
, ,∴
,∴ ,又∵
,又∵ 平面
平面 ,
, ,∴
,∴ ,∴二面角
,∴二面角 的正切值的大小为
的正切值的大小为 。………………………8分
。………………………8分
(Ⅲ)过点 做
做 ∥
∥ ,交
,交 于点
于点 ,∵
,∵ 平面
平面 ,∴
,∴ 为
为 在平面
在平面 内的射影,∴
内的射影,∴ 为
为 与平面
与平面 所成的角,………………………10分
所成的角,………………………10分
 ∵
∵ ,∴
,∴ ,又∵
,又∵ ∥
∥ ,∴
,∴ 和
和 与平面
与平面 所成的角相等,∴
所成的角相等,∴ 与平面
与平面 所成角的正切值为
所成角的正切值为 。………………………12分
。………………………12分
解法2:如图建立空间直角坐标系,(Ⅰ)∵, ,∴点
,∴点 的坐标分别是
的坐标分别是 ,
, ,
,
 ,∴
,∴ ,
, ,设
,设 ,∵
,∵ 平面
平面 ,∴
,∴ ,∴
,∴ ,取
,取 ,∴
,∴ ,∴
,∴ 。………………………4分
。………………………4分
(Ⅱ)设二面角 的大小为
的大小为 ,∵平面
,∵平面 的法向量是
的法向量是 ,平面
,平面 的法向量是
的法向量是 ,∴
,∴ ,∴
,∴ ,∴二面角
,∴二面角 的正切值的大小为
的正切值的大小为 。………………………8分
。………………………8分
(Ⅲ)设 与平面
与平面 所成角的大小为
所成角的大小为 ,∵平面
,∵平面 的法向量是
的法向量是 ,
, ,∴
,∴ ,∴
,∴ ,∴
,∴ 与平面
与平面 所成角的正切值为
所成角的正切值为 。………………………12分
。………………………12分
21.解析:(Ⅰ)设抛物线方程为 ,将
,将 代入方程得
代入方程得
所以抛物线方程为 。………………………2分
。………………………2分
由题意知椭圆的焦点为 、
、 。
。
设椭圆的方程为 ,
,
∵过点 ,∴
,∴ ,解得,
,解得, ,
, ,
,
∴椭圆的方程为 。………………………5分
。………………………5分
(Ⅱ)设 的中点为
的中点为 ,
, 的方程为:
的方程为: ,
,
以 为直径的圆交
为直径的圆交 于
于 两点,
两点, 中点为
中点为 。
。
设 ,则
,则
∵
 ………………………8分
………………………8分
∴
 ………………………10分
………………………10分
当 时,
时, ,
, ,
,
此时,直线 的方程为
的方程为 。………………………12分
。………………………12分
22.(12分)解析:(Ⅰ)∵ 是偶函数,∴
是偶函数,∴ ,
,
又∵ ∴
∴ ,
, ,………………………2分
,………………………2分
由 得,
得, ,
,
∵ 时,
时, ;
; 时,
时, ;
; 时,
时, ;∴
;∴ 时,函数
时,函数 取得极大值
取得极大值 ,
, 时,函数
时,函数 取得极小值
取得极小值 。………………………5分
。………………………5分
(Ⅱ)∵ 在区间
在区间 上为增函数,∴
上为增函数,∴ 在
在 上恒成立,∴
上恒成立,∴
 且
且 在区间
在区间 上恒成立,………………………7分
上恒成立,………………………7分
∴
∴ ……………………9分
……………………9分
又∵ =
= ,∵
,∵
∴ ,∴
,∴ 的取值范围是
的取值范围是 。………………………12分
。………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com