
青岛市2009年高三模拟练习
数学 (文科) 2009.05
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
注意事项:
1.答卷前,考生务必用2B铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试题卷上.
3.第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.  为虚数单位,则复数
为虚数单位,则复数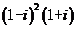 的值为
的值为
A.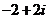 B.
B.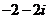 C.
C.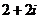 D.
D.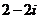
2. 已知集合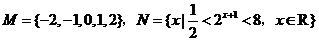 ,则
,则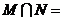
A.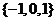 B.
B.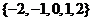 C.
C.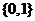 D.
D.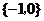
3.一组数据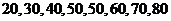 的平均数、中位数、众数的大小关系是
的平均数、中位数、众数的大小关系是
A.平均数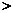 中位数
中位数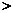 众数 B.平均数
众数 B.平均数 中位数
中位数 众数
众数
C.中位数 众数
众数 平均数 D.众数
平均数 D.众数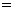 中位数
中位数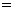 平均数
平均数
4.汽车经过启动、加速行驶、匀速行 驶、减速行驶之后停车,若把这一过程中汽车的行驶路程
驶、减速行驶之后停车,若把这一过程中汽车的行驶路程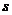 看作时间
看作时间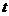 的函数,其图象可能是
的函数,其图象可能是
 |
5.通过调查发现某中学女同学的体重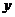
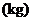 与身高
与身高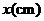 有线性相关关系,且满足
有线性相关关系,且满足
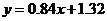 ,则当变量
,则当变量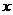 增加一个单位时
增加一个单位时
A.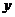 平均增加
平均增加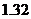 个单位 B.
个单位 B.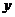 平均减少
平均减少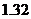 个单位
个单位
C.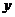 平均增加
平均增加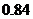 个单位 D.
个单位 D.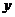 平均减少
平均减少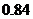 个单位
个单位
6.如右图为长方体木块堆成的几何体的三视图,则组成此几何体的长方体木块块数共有
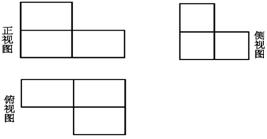 A.
A.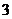 块 B.
块 B.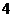 块
C.
块
C.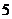 块
D.
块
D.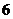 块
块
7. 已知各项不为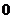 的等差数列
的等差数列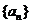 ,满足
,满足
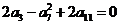 ,数列
,数列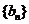 是等比数列,且
是等比数列,且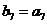 ,则
,则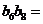
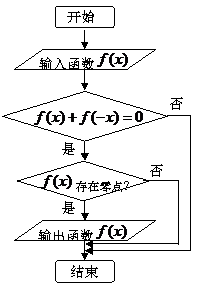 A.
A.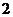 B.
B.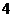 C.
C.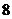 D.
D.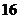
8. 某程序框图如图所示,现输入如下四个函数,则可以输出的函数是
A.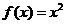 B.
B.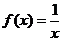
C.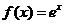 D.
D.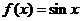
9. 设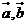 都是非零向量,那么命题“
都是非零向量,那么命题“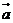 与
与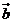 共线”是命题“
共线”是命题“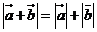 ”的
”的
A. 充分不必要条件;B. 必要不充分条件;
C. 充要条件 ; D. 既不充分又不必要条件
10. 已知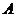 船在灯塔
船在灯塔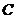 北偏东
北偏东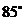 且
且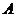 到
到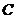 的距离为
的距离为 ,
,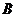 船在灯塔
船在灯塔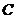 西偏北
西偏北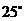 且
且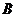 到
到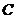 的距离为
的距离为 ,则
,则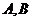 两船的距离为www.1010jiajiao.com
两船的距离为www.1010jiajiao.com
A. 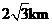 B.
B. 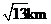 C.
C. 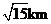 D
D .
.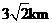
11.已知双曲线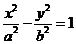 的一条渐近线方程为
的一条渐近线方程为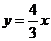 ,则双曲线的离心率为
,则双曲线的离心率为
A.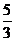 B.
B.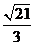 C.
C.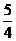 D.
D.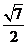
12. 已知直线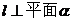 ,直线
,直线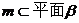 ,给出下列命题中
,给出下列命题中
①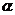 ∥
∥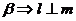 ;②
;②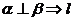 ∥
∥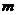 ;③
;③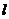 ∥
∥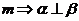 ;④
;④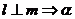 ∥
∥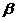

其中正确的是
A.①②③ B.②③④ C.②④ D.①③ 学科
学科
网第Ⅱ卷(非选择题 共90分)
二、填空:本大题共4小题,每小题4分,共16分.
13.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
 |
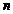 个图案中有白色地面砖的块数是
.
个图案中有白色地面砖的块数是
. 14.已知函数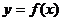
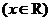 满足
满足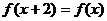 ,且
,且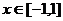 时,
时,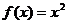 ,则
,则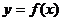 与
与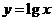 的图象的交点个数为
.
的图象的交点个数为
. 学科网
学科网
15.已知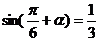 ,则
,则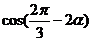 的值等于
.
的值等于
.
16.实数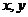 满足不等式组
满足不等式组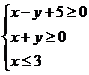 ,那么目标函数
,那么目标函数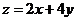 的最小值是______.
的最小值是______.
三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知向量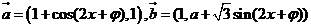 (
(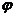 为常数且
为常数且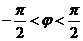 ),函数
),函数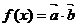 在
在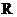 上的最大值为
上的最大值为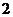 .
.
(Ⅰ)求实数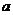 的值;
的值;
(Ⅱ)把函数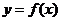 的图象向
的图象向 右平移
右平移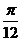 个单位,可得函数
个单位,可得函数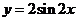 的图象,求函数
的图象,求函数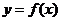 的解析式及其单调增区间.
的解析式及其单调增区间.
18. (本小题满分12分)
先后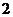 次抛掷一枚骰子,将得到的点数分别记为
次抛掷一枚骰子,将得到的点数分别记为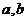 .
.
(Ⅰ)设函数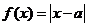 ,函数
,函数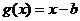 ,令
,令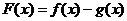 ,求函数
,求函数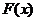 有且只有一个零点的概率;
有且只有一个零点的概率;
(Ⅱ)将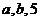 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
 19.(本小题满分12分)
19.(本小题满分12分)
如图1所示,在边长为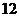 的正方形
的正方形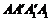 中,
中,
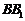
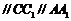 ,且
,且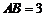 ,
,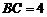 ,
,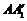 分别
分别
交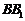
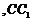 点于
点于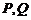 ,将该正方形沿
,将该正方形沿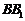 、
、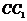
折叠,使得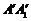 与
与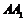 重合,构成如图2所示的
重合,构成如图2所示的
三棱柱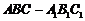 中
中
(Ⅰ)求证: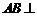
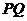 ;
;
(Ⅱ)在底边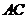 上是否存在一点
上是否存在一点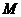 ,满足
,满足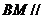 平面
平面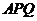 ,若存在试确定点
,若存在试确定点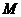 的位置,若不存在请说明理由.
的位置,若不存在请说明理由.
20.(本小题满分12分)
在数列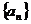 中,
中,
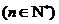 .
.
(Ⅰ)求证:数列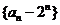 为等差数列;
为等差数列;
(Ⅱ)设数列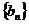 满足
满足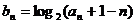 ,若
,若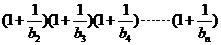
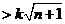 对一切
对一切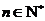 且
且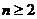 恒成立,求实数
恒成立,求实数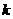 的取值范围.
的取值范围.
21.(本小题满分12分)已知函数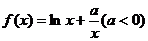 ,直线
,直线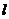 与函数
与函数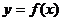 图象相切.
图象相切.
(Ⅰ)求直线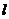 的斜率
的斜率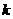 的取值范围;
的取值范围;
(Ⅱ)设函数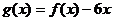 ,已知函数
,已知函数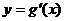 的图象经过点
的图象经过点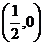 ,求函数
,求函数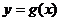 的极值.
的极值.
22. (本小题满分14分)已知圆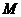 过两点
过两点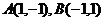 ,且圆心
,且圆心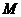 在
在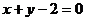 上.
上.
(Ⅰ)求圆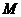 的方程;
的方程;
(Ⅱ)设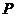 是直线
是直线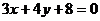 上的动点,
上的动点,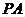 、
、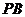 是圆
是圆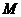 的两条切线,
的两条切线,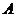 、
、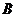 为切点,求四边形
为切点,求四边形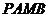 面积的最小值.
面积的最小值.
青岛市2009年高三模拟练习
数学(文科)答案及评分标准 2009.05
DADAC,BDDBB,AD
二、填空:本大题共4小题,每小题4分,共16分.
13.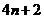 ; 14.
; 14.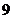 ;
; 学科网
15.
学科网
15.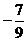 ; 16.
; 16.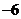
三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)
解:(Ⅰ) …3分
…3分
因为函数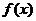 在
在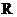 上的最大值为
上的最大值为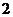 ,所以
,所以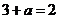 ,即
,即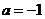 …5分
…5分
(Ⅱ)由(Ⅰ)知:
把函数 的图象向右平移
的图象向右平移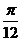 个单位
个单位
可得函数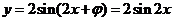 ………………………………8分
………………………………8分
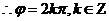
又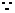
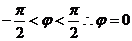
 …………………………10分
…………………………10分
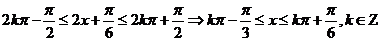
所以,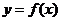 的单调增区间为
的单调增区间为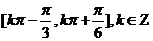 …………………………12分
…………………………12分
18. (本小题满分12分)
解:(Ⅰ)先后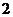 次抛掷一枚骰子,将得到的点数分别记为
次抛掷一枚骰子,将得到的点数分别记为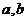 ,事件总数为
,事件总数为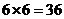 .
.
…………………-2分
∵函数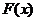 有且只有一个零点
有且只有一个零点
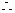 函数
函数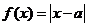 与函数
与函数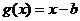 有且只有一个交点
有且只有一个交点
所以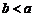 ,且
,且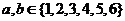
∴满足条件的情况有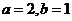 ;
;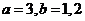 ;
;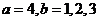 ;
;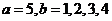 ;
;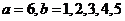 .共
.共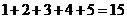 种情况. -------6分
种情况. -------6分
∴函数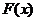 有且只有一个零点的概率是
有且只有一个零点的概率是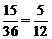 --------7分
--------7分
(Ⅱ)先后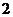 次抛掷一枚骰子,将得到的点数分别记为
次抛掷一枚骰子,将得到的点数分别记为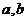 ,事件总数为
,事件总数为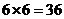 .
.
∵三角形的一边长为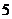 ∴当
∴当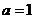 时,
时,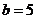 ,
,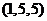 ,
, 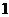 种 ; 当
种 ; 当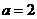 时,
时,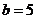 ,
,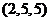 ,
, 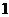 种; 当
种; 当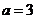 时,
时,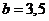 ,
,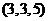 ,
,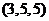 ,
, 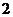 种; 当
种; 当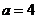 时,
时,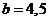 ,
,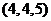 ,
,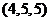 ,
,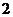 种; 当
种; 当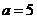 ,
,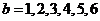 ,
,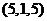 ,
,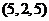 ,
,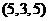 ,
,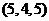 ,
,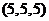 ,
,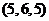 ,
, 种; 当
种; 当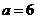 ,
,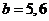 ,
,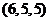 ,
, ,
,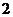 种
种
故满足条件的不同情况共有 种---------11分
种---------11分
答:三条线段能围成不同的等腰三角形的概率为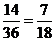 . -----------12分
. -----------12分
19.(本小题满分12分)
解:(Ⅰ)证明:因为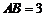 ,
,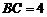 ,
,
所以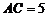 ,从而
,从而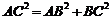 ,即
,即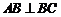 .………………………3分
.………………………3分
又因为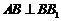 ,而
,而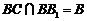 ,
,
所以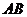
 平面
平面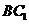
又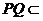 平面
平面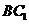
所以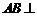
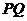 ;………………5分
;………………5分
(Ⅱ)解:假设存在一点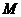 满足
满足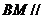 平面
平面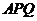 ,过
,过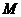 作
作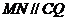 交
交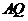 于
于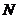
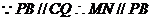 …………………………8分
…………………………8分
连接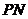 ,因为
,因为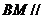 平面
平面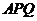
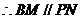
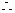 四边形
四边形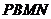 为平行四边形…………………………10分
为平行四边形…………………………10分
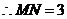 ,
,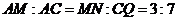
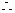 当点
当点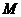 满足
满足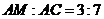 时,
时, 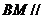 平面
平面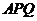 .…………………………12分
.…………………………12分
20.(本小题满分12分)
解:(Ⅰ)由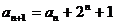 变形得:
变形得: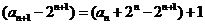
即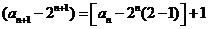
所以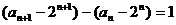 …………………4分
…………………4分
故数列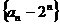 是以
是以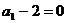 为首项,
为首项,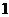 为公差的等差数列………………………5分
为公差的等差数列………………………5分
(Ⅱ)由(Ⅰ)得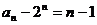 …………………………6分
…………………………6分
所以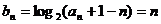 …………………………7分
…………………………7分
设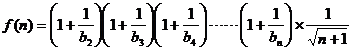 ………………8分
………………8分
则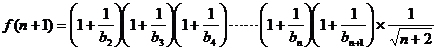
两式相除得: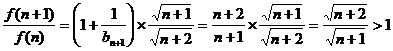 ……10分
……10分
所以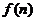 是关于
是关于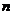 的单调递增函数,则
的单调递增函数,则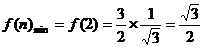
故实数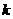 的取值范围是
的取值范围是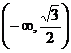 …………………………12分
…………………………12分
21.(本小题满分12分)
解:(Ⅰ)设切点坐标为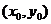 ,由
,由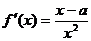 得:………………………2分
得:………………………2分
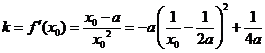 …………………………4分
…………………………4分
根据题意知: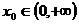 ,即
,即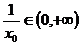 ,所以
,所以
又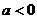 ,则
,则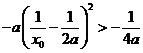 ,即
,即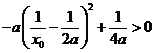
所以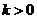 …………………………6分
…………………………6分
(Ⅱ)显然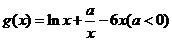 的定义域为
的定义域为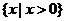 …………………………7分
…………………………7分
根据(Ⅰ)与题意知: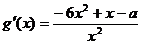 …………………………8分
…………………………8分
又因为函数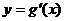 的图象经过点
的图象经过点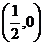 ,代入
,代入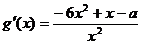 求得:
求得: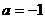
则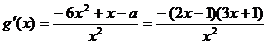 …………………………10分
…………………………10分
由此可知:当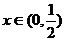 时,有
时,有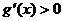 ,此时
,此时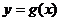 为单调增函数;
为单调增函数;
当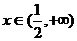 时,有
时,有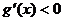 ,此时
,此时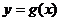 为单调减函数;
为单调减函数;
所以函数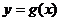 在区间
在区间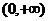 上只有极大值,
上只有极大值,
即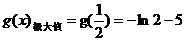 .…………………………12分
.…………………………12分
22. (本小题满分14分)
解:(Ⅰ)设圆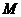 的方程为:
的方程为: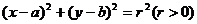 …………………………1分
…………………………1分
根据题意得: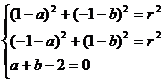 …………………………4分
…………………………4分
解得;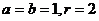
故所求圆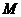 的方程为:
的方程为: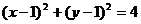 …………………………6分
…………………………6分
(Ⅱ)因为四边形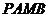 面积
面积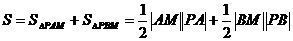 ………8分
………8分
又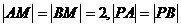
所以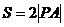 ,而
,而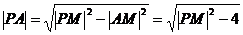
即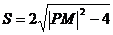 …………………………10分
…………………………10分
因此要求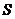 的最小值,只需求
的最小值,只需求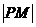 的最小值即可
的最小值即可
即在直线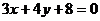 上找一点
上找一点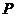 ,使得
,使得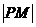 的值最小…………………………12分
的值最小…………………………12分
所以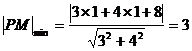
所以四边形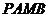 面积的最小值为
面积的最小值为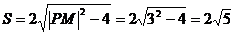 ………14分
………14分 www.1010jiajiao.com
www.1010jiajiao.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com