|
试题详情
A.4 B.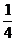 C.―
4 D. C.―
4 D.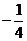 试题详情
7. 2007―2008学年湖北省黄州西湖中学二月月考试卷 试题详情
已知等比数列 的首项为8, 的首项为8, 是其前n项的和,某同学经计算得S2=20, 是其前n项的和,某同学经计算得S2=20, S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为( ) A. S1 B. S2 C. S3 D. S4 试题详情
解析:显然S1是正确的.假设后三个数均未算错,则a1=8,a2=12,a3=16,a4=29,可知a22≠a1a3,故S2、S3中必有一个数算错了.若S2算错了,则a4=29=a1q3, ,显然S3=36≠8(1+q+q2),矛盾.只可能是S3算错了,此时由a2=12得 ,显然S3=36≠8(1+q+q2),矛盾.只可能是S3算错了,此时由a2=12得 ,a3=18,a4=27,S4=S2+18+27=65,满足题设.选C. ,a3=18,a4=27,S4=S2+18+27=65,满足题设.选C. 评析:本题考查等比数列的基本概念与性质和学生推理的能力. 试题详情
8. 上海市嘉定一中2007学年第一学期高三年级测试(二) 试题详情
等差数列{an}共有2n项,其中奇数项的和为90,偶数项的和为72,且 ,则该数列的公差为 ( ) ,则该数列的公差为 ( ) A.3 B.-3 C.-2 D.-1 试题详情
9. 2008年天津市十二区县重点学校高三毕业班联考(一) 试题详情
试题详情
10. 广东省梅州揭阳两市四校2008届高三第三次联考数学理科试卷 试题详情
等差数列{an}、{bn}的前n项和分别为Sn、Tn,且 ,则使得 ,则使得 为整数的正整数n的个数是( ) 为整数的正整数n的个数是( ) A.3 B.4 C.5 D.6 试题详情
试题详情
 , ,  ; ; 试题详情
11. 已知首项为正数的等差数列{an}满足:a2005+a2006>0,a2005?a2006<0,则使前项Sn>0成立的最大自然数n是
A. 4009 B.4010 C. 4011
D.4012
由题意知:等差数列中,从第1项到第2005项是正数,且从第2006项开始为负数,S4010=2005(a1+a4010)=2005(a2005+a2006)>0, 试题详情
S4011==4011a2006<0, 故n的最大值为4010. 试题详情
另解:由题意可得:等差数列中,从第1项到第2005项是正数,且从第2006项开始是负数,则所有的正项的和为Sn的最大值,即当n=2005时,取得最大值,显然Sn是关于n的缺常数项的二次函数,且开口向下,所以第2005项离对称轴最近,故其对称轴介于2005到2005.5之间,又因为二次函数的图象与x轴的一个交点是(0,0),则设另一个交点(x,0),x应介于4010到4011之间.所以使Sn>0的最大自然数是4010,故选B.
本小题结论可以推广成一般结论:等差数列中,a1>0,ak+ak+1>0,且akak+1<0,则使前n项和Sn>0的最大自然数n是2k.. 试题详情
12. 如图,在杨辉三角中,斜线l上方,从1开始箭头所示的数组成一个锯齿数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于____________. 1 1
1
l 试题详情
  1 2 1
1 2 1
试题详情
  1 3 3 1 1 3 3 1
试题详情
  1 4 6 4 1
1 4 6 4 1
试题详情
  1
5 10 10 5 1 1
5 10 10 5 1
… … …
… … … … 试题详情
283 [解析] 由条件知道:该数列的奇数项分别为1,3,6,10,15,21,28,36,45,55,…,偶数项分别为3,4,5,6,7,8,9,10,11,…,把奇数项的前10项与偶数项的前9项相加即得S19=283. 试题详情
13. 下图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖___________块.(用含n的代数式表示) 试题详情
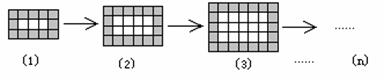
第(1)、(2)、(3)…个图案黑色瓷砖数依次为:15-3=12;24-8=16;35-15=20;… 由此可猜测第(n)个图案黑色瓷砖数为:12+(n-1)×4=4n+8 试题详情
14. 已知等差数列{an}中,a2+a8=8,则该数列前9项和S9等于( )。 A.18 B.27 C.36
D.45 试题详情
C 解:在等差数列{an}中,a2+a8=8,∴  ,则该数列前9项和S9= ,则该数列前9项和S9= =36, =36, 故选择答案C 试题详情
 15. 探索以下规律: 15. 探索以下规律:
试题详情
则根据规律,  从2006到2008,箭头的方向依次是(
) 从2006到2008,箭头的方向依次是(
) 试题详情
试题详情
试题详情
试题详情
试题详情
①若数列 既是等差数列又是等比数列,则 既是等差数列又是等比数列,则 ; ; 试题详情
②若 ,则数列 ,则数列 是等差数列; 是等差数列; 试题详情
③若 ,则数列 ,则数列 是等比数列. 是等比数列. 这些命题中,真命题的个数是 A.0 B.1 C.2 D.3 试题详情
试题详情
【总结点评】本题主要考查等差、等比数列的概念, 与 与 的关系,思维的灵活性. 的关系,思维的灵活性. 试题详情
试题详情
C 由 ,知 ,知 . ∴ . ∴ ,故选C. ,故选C. 【总结点评】本题主要考查等差数列的性质,求和公式. 要求学生能够运用性质简化计算. 试题详情
试题详情
2, ( ( ) ) 试题详情
(注意:答案不唯一,如写成 即可) 即可) 试题详情
20. 等差数列 的值为 的值为 A.―2006 B.2006 C.―2008 D.2008 试题详情
21.在数列{an}中,a1=2,an+1= >0,则a2008= ( ) >0,则a2008= ( ) 试题详情
A. B.
B. 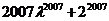 试题详情
C.
 D. D.
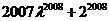 由 试题详情
an+1= - - 为等差数列,且公差为1,首项为0,则 试题详情
 . .
试题详情
22. 在等差数列{an}中,a1= ,从第5项开始大于1,记其前n项和为Sn,若P= ,从第5项开始大于1,记其前n项和为Sn,若P=  ,则P的取值范围是
(
) ,则P的取值范围是
(
) 试题详情
试题详情
试题详情
又nan+Sn=n[a1+(n-1)d]+na1+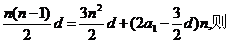 试题详情
 ,故选A, ,故选A,
试题详情
试题详情
试题详情
试题详情
24. 已知等比数列{ }的前n项和为Sn,且S3=7a1,则数列{ }的前n项和为Sn,且S3=7a1,则数列{ }的公比q的值为 }的公比q的值为 A.2 B.3 C.2或-3 D.2或3 试题详情
25. 已知等差数列 ,则n的值为 ,则n的值为 A.18 B.17 C.16 D.15 试题详情
试题详情
三、解答题:
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(2)对于(1)中 ,不等式化为: ,不等式化为: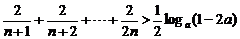 试题详情
对任意正整数 恒成立 ---------------------------------------------------5分 恒成立 ---------------------------------------------------5分 试题详情
设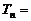  , , 试题详情
 ,数列 ,数列 单调递增,-6分 单调递增,-6分
试题详情
所以 ,要使不等式恒成立,只要 ,要使不等式恒成立,只要 -------------7分 -------------7分 试题详情
试题详情
所以,使不等式对于任意正整数恒成立的 的取值范围是: 的取值范围是: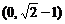 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(2) , ,  -------------------------------------------------5分 -------------------------------------------------5分 试题详情
试题详情
试题详情
(3)对于(1)中 ,不等式化为: ,不等式化为: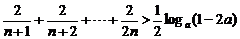 试题详情
对任意正整数 恒成立 -------------------------------------------------11分 恒成立 -------------------------------------------------11分 试题详情
设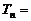  , , 试题详情
试题详情
试题详情
所以,使不等式对于任意正整数恒成立的 的取值范围是: 的取值范围是: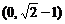 上海市静安区2007学年第一学期高三期末质量监控考试数学试题 试题详情
试题详情
(1)
试写出销售量 与 与 的函数关系式; 的函数关系式; 试题详情
(2)
当 时公司应作几千元广告,销售量为多少件时,才能使去掉广告费用后的获利最大? 时公司应作几千元广告,销售量为多少件时,才能使去掉广告费用后的获利最大? 试题详情
试题详情
试题详情
(2) ,设获利为 ,设获利为 元,则有 元,则有 试题详情
试题详情
试题详情
所以 时, 时, 最大,此时 最大,此时 . . 即该厂家应做5千元的广告,销售量为7875件产品时,能使获利最大. 试题详情
试题详情
 确定.记 确定.记 .求: .求:
试题详情
(1) 时 时 的值; 的值; 试题详情
(2) 最小时 最小时 的值. 的值. 试题详情
(文)已知等差数列{an}的首项a1=0且公差d≠0, bn=2 (n∈N*),Sn是数列{bn}的前n项和.
(n∈N*),Sn是数列{bn}的前n项和. (1) 求Sn; 试题详情
(2)
设Tn= (n∈N*),当d>0时,求
(n∈N*),当d>0时,求 . . 试题详情
(理)(1) , , 试题详情
 , ,
试题详情
试题详情
= . . 试题详情
(2) 试题详情
= 试题详情
试题详情
所以当 时, 时, 最小. 最小. 试题详情
(文)(1) an=(n-1)d,bn=2 =2(n-1)d?? =2(n-1)d??
Sn=b1+b2+b3+…+bn=20+2d+22d+…+2(n-1)d? 试题详情
由d≠0得2d≠1,∴Sn= . .
试题详情
(2) Tn= , ,
当d>0时,2d>1
试题详情
试题详情
试题详情
试题详情
试题详情
(2)设数{ }的通项为 }的通项为 ,求M的取值范围;(4分) ,求M的取值范围;(4分) 试题详情
(1)设等差数列 的公差是d ,则a1+2d=4,3a1+3d=18,解得a1=8,d =-2, 的公差是d ,则a1+2d=4,3a1+3d=18,解得a1=8,d =-2, 试题详情
所以 ,(2分), ,(2分), 试题详情
试题详情
得 适合条件①. (4分); 适合条件①. (4分); 试题详情
又 , , 所以当n = 4或5时,Sn取得最大值20,即Sn ≤ 20,适合条件②, (3分), 试题详情
综上,{ } } . (1分) . (1分) 试题详情
(2)因为 ,(2分), ,(2分), 试题详情
所以当n≥3时, ,此时数列{bn}单调递减;(1分) ,此时数列{bn}单调递减;(1分) 试题详情
当n = 1,2时, ,即b1<b2<b3, ,即b1<b2<b3, 试题详情
因此数列{bn}中的最大项是b3=7,所以M≥7.(3分) 试题详情
试题详情
试题详情
(1)设 ,求数列 ,求数列 的通项公式; 的通项公式; 试题详情
(2)求数列 和 和 的通项公式。 的通项公式。 试题详情
(1)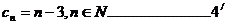 试题详情
(2)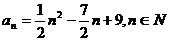  试题详情
试题详情
试题详情
试题详情
试题详情
(3)对一般的首项为 ,公差为 ,公差为 的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论. 的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论. 试题详情
试题详情
试题详情
试题详情
(2)当 为正整数时, 为正整数时,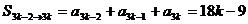 试题详情
 ,∴ ,∴  (常数) (常数) 试题详情
试题详情
(3)(理)可以从多个方面加以推广.对一般的以 为首项, 为首项, 为公差的等差数列, 为公差的等差数列, 如照抄(2)中的问题(即三项之和)得3分,证明结论得4分,共得7分; 如对(2)中的问题有所改变,如改为四项之和,得4分,证明得4分,共8分; 试题详情
如对(2)中的问题有所创新,如:“对于任意给定的正整数 ,判断数列 ,判断数列 试题详情
试题详情
8. 新余市2007――2008学年度上学期高三年级期末质量检测 试题详情
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以 表示第 表示第 个图的蜂巢总数. 个图的蜂巢总数. 试题详情
试题详情
(1) 试给出 的值,并求 的值,并求 的表达式(不要求证明); 的表达式(不要求证明); 试题详情
(2) 证明: . . 试题详情
解: ⑴ …………………………………………………(4分) …………………………………………………(4分) 试题详情
由于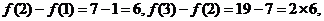 试题详情
试题详情
因此,当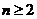 时,有 时,有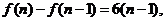 试题详情
所以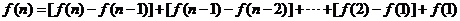 试题详情
 . .
试题详情
又 ,所以 ,所以 . ……………(7分) . ……………(7分) (注:直接给出结果也给分) 试题详情
⑵当 时, 时, . …………(10分) . …………(10分) 试题详情
所以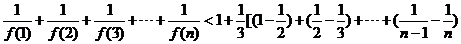 试题详情
 . ……………………………………………(12分) . ……………………………………………(12分)
试题详情
9. 常德市2007-2008学年度上学期高三水平检测考试题 试题详情
试题详情
(1)
求 的值,并证明:当n>2时有 的值,并证明:当n>2时有 ; ; 试题详情
(2)
求证: . . 试题详情
试题详情
当n>2时有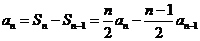 试题详情
∴ ……………………………6分
……………………………6分 试题详情
(2)由(1)知n>2时, ……………8分 ……………8分 试题详情
又 =0, =0,  =2也适合上式, =2也适合上式, 试题详情
∴ ∴ ∴ ……………………10分 ……………………10分 试题详情
∴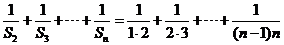 试题详情
=1- <1……………………………………………12分 <1……………………………………………12分 试题详情
试题详情
(1)求向量 ; ; 试题详情
试题详情
解:(1)设 =(x,y),则 =(x,y),则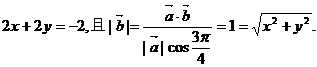 试题详情
试题详情
∴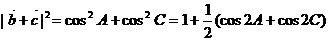 试题详情
试题详情
∴ ∴ ∴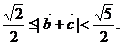 试题详情
试题详情
(1)求 的值. 的值. 试题详情
试题详情
(3)若自然数 ( ( 为正整数) 为正整数) 试题详情
试题详情
试题详情
(理科考生做)求 的所有可能值. 的所有可能值. 试题详情
试题详情
则 试题详情
试题详情
则 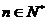 试题详情
又  则 则 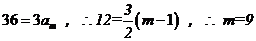 试题详情
试题详情
则 试题详情
试题详情
又因为  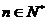 试题详情
(理科)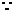  成等比数列, 成等比数列, 试题详情
试题详情
又 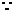  试题详情
试题详情
试题详情
试题详情
试题详情
12. 山东省潍坊市2007―2008学年度高三第一学期期末考试 试题详情
已知数列 ,设 ,设 试题详情
 ,数列 ,数列 。 。 试题详情
(1)求证: 是等差数列; 是等差数列; 试题详情
(2)求数列 的前n项和Sn; 的前n项和Sn; 试题详情
(3)若 一切正整数n恒成立,求实数m的取值范围。 一切正整数n恒成立,求实数m的取值范围。 试题详情
解:(1)由题意知, ……………………1分 ……………………1分 试题详情
试题详情
试题详情
∴数列 的等差数列……………………4分 的等差数列……………………4分 试题详情
(2)由(1)知,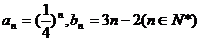 试题详情
 …………………………5分 …………………………5分
试题详情
试题详情
于是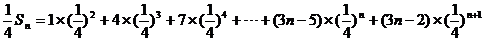 试题详情
两式相减得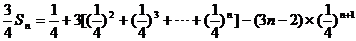 试题详情
试题详情
 ……………………8分 ……………………8分
试题详情
(3)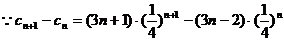 试题详情
试题详情
∴当n=1时,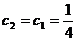 试题详情
当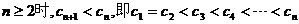 试题详情
∴当n=1时, 取最大值是 取最大值是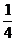 试题详情
又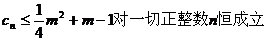 试题详情
试题详情
即 ……………………12分 ……………………12分 试题详情
13. 武汉市2008届高中毕业生二月调研测试文科数学试题 试题详情
试题详情
试题详情
解:(1)数列 的前n项之和 的前n项之和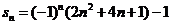 试题详情
在n=1时,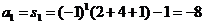 试题详情
在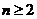 时, 时,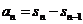 试题详情
试题详情
试题详情
而n=1时, 满足 满足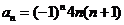 试题详情
故所求数列 通项 通项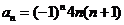 ………………………………(7分) ………………………………(7分) 试题详情
(2)∵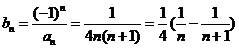 试题详情
因此数列 的前n项和 的前n项和 ………………………(12分) ………………………(12分) 试题详情
14. 武汉市2008届高中毕业生二月调研测试理科数学试题 试题详情
试题详情
试题详情
(1)猜想出数列 的通项公式并用数学归纳法证明之; 的通项公式并用数学归纳法证明之; 试题详情
(2)求证: , , . . 试题详情
试题详情
下面用数学归纳法证明 10当n=1时 a1=t―1 满足条件
10当n=1时 a1=t―1 满足条件 试题详情
试题详情
由10、20知 …………………………………………………………(7分) …………………………………………………………(7分) 试题详情
试题详情
而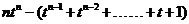 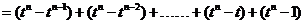 试题详情
试题详情
试题详情
15. 2008年成都名校联盟高考数学冲刺预测卷二 试题详情
试题详情
试题详情
(1)∵  , , , , 由已知a<b<a+b<ab<a+2b, 试题详情
∴ 由a+2b<ab,a、 得 得 . . 试题详情
∵  , ∴ a≥2. , ∴ a≥2. 试题详情
又得 ,而 ,而 , ∴ b≥3. , ∴ b≥3. 试题详情
再由ab<a+2b,b≥3,得 . . 试题详情
试题详情
(2)设 ,即 ,即 . . 试题详情
∴  , , . . 试题详情
试题详情
故 . . 试题详情
试题详情
试题详情
(1)证明数列 是公比为2的等比数列。 是公比为2的等比数列。 试题详情
(2)求 关于n的表达式。 关于n的表达式。 试题详情
试题详情
(1)证明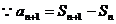 试题详情
由已知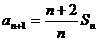 试题详情
 (2分) (2分)
试题详情
试题详情
试题详情
(2)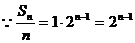 试题详情
 (3分) (3分)
试题详情
(3)猜测:存在 (1分) (1分) 试题详情
试题详情
 (1分) (1分)
试题详情
试题详情
定义 为 为 中的最小值,若 中的最小值,若 试题详情
试题详情
(1)画出 的图象,并写出 的图象,并写出 的解析式。 的解析式。 试题详情
试题详情
(3)求使对一切的 恒成立的实数k的取值范围。 恒成立的实数k的取值范围。 试题详情
试题详情
试题详情
 (2分) (2分)
(2)由图可知: 试题详情
试题详情
 (2分) (2分)
试题详情
(3)(理)①当 (1分) (1分) 试题详情
②当 (1分)
(1分) 试题详情
③当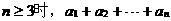 试题详情
试题详情
 (1分)
(1分)
试题详情
故命题  恒成立。 恒成立。 试题详情
 (1分) (1分) 试题详情
试题详情
 (1分) (1分)
试题详情
由①②③知符合题意的k的取值范围为 。 (1分) 。 (1分) 试题详情
(文)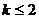 试题详情
试题详情
试题详情
解:由题意得: …………2分 …………2分 试题详情
∵ 垂直, 垂直, 试题详情
∴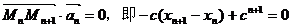 试题详情
∵ …………4分 …………4分 试题详情
∴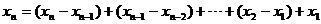 试题详情
 …………6分 …………6分
试题详情
当c=1时, …………8分 …………8分 试题详情
当c≠1时, 试题详情
试题详情
试题详情
 …………12分 …………12分
试题详情
试题详情
试题详情
(1) 求函数 的解析式; 的解析式; 试题详情
试题详情
试题详情
(2)  , ………………………………………………5分 , ………………………………………………5分 试题详情
 , ,
试题详情
 , …………………………………10分 , …………………………………10分
试题详情
又 满足上式.
所以 满足上式.
所以 . …………………14分 . …………………14分 试题详情
20. 江苏省省阜中2008届高三第三次调研考试数学(文科)试题 试题详情
设集合W是满足下列两个条件的无穷数列 的集合:① 的集合:① ; ② ; ② M是与n无关的常数. 试题详情
试题详情
(2)设数{ }的通项为 }的通项为 ,求M的取值范围;(4分) ,求M的取值范围;(4分) 试题详情
(1)设等差数列 的公差是d ,则a1+2d=4,3a1+3d=18,解得a1=8,d =-2, 的公差是d ,则a1+2d=4,3a1+3d=18,解得a1=8,d =-2, 试题详情
所以 ,(2分), ,(2分), 试题详情
试题详情
得 适合条件①. (4分); 适合条件①. (4分); 试题详情
又 , , 所以当n = 4或5时,Sn取得最大值20,即Sn ≤ 20,适合条件②, (3分), 试题详情
综上,{ } } . (1分) . (1分) 试题详情
(2)因为 ,(2分), ,(2分), 试题详情
所以当n≥3时, ,此时数列{bn}单调递减;(1分) ,此时数列{bn}单调递减;(1分) 试题详情
当n = 1,2时, ,即b1<b2<b3, ,即b1<b2<b3, 试题详情
因此数列{bn}中的最大项是b3=7,所以M≥7.(3分) 试题详情
试题详情
已知正项数列{an}的前n项和
(1)求数列{an}的通项公式 试题详情
(2)定理:若函数f(x)在区间D上是凹函数,且f’(x)存在,则当x1>x2 (x1,x2∈D)时,总有 ,已知函数y=xn+1 (n∈N*)是(0,+ ,已知函数y=xn+1 (n∈N*)是(0,+ )上的凹函数,请根据上述定理,判断bn与bn+1的大小 )上的凹函数,请根据上述定理,判断bn与bn+1的大小 试题详情
(3)求证: (1)n=1时,a1= (1)n=1时,a1= 或a1=1 或a1=1 试题详情
∵{an}是正项数列,∴a1=1,当n≥2时, ,整理, ,整理, 试题详情
得 试题详情
∵{an}是正项数列, ∴
∴数列{an}是以1为首项,1为公差的等差数列,从而an=n, ∴an
=n (n∈N*) 试题详情
试题详情
令 ,得(n+1)x2-nx1=1 ,得(n+1)x2-nx1=1 试题详情
试题详情
(3)由(2),得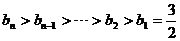 试题详情
试题详情
试题详情
⑴求数列 的通项公式; 的通项公式; 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
 (4分)
(4分)
试题详情
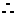  成等比数列 成等比数列
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
⑴求证:数列 是等比数列; 是等比数列; 试题详情
试题详情
证明:⑴由条件得 显然 显然 …1 分 …1 分 试题详情
试题详情
∵ 为常数, ………………5分 为常数, ………………5分 试题详情
∴所以数列 是公比为2的等比数列
………………7分 是公比为2的等比数列
………………7分 ⑵由⑴得: 试题详情
 ,
………………9分 ,
………………9分
试题详情
∴ …………10分
…………10分 试题详情
∵ , , 试题详情
∴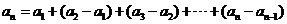 试题详情
 …14分 …14分
试题详情
∴ 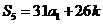 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
当 时, 时,  ① ① 试题详情
 ② ②
试题详情
由①-②得,  ………(3分) ………(3分) 试题详情
试题详情
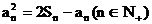  ………(5分) ………(5分)
试题详情
(2)由(1)知,  ③ ③ 试题详情
当 时, 时,  ④ ④ 由③-④得, 试题详情
试题详情
试题详情
公差为1, 可得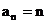  ………(10分) ………(10分) 试题详情
(3) ∵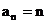 , ∴ , ∴ ………(11分) ………(11分) 试题详情
∴ , , 试题详情
∴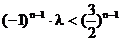  ⑤………(12分) ⑤………(12分) 试题详情
试题详情
依题意, ⑥式对 都成立, 当 都成立, 当 时, 时, 试题详情
试题详情
试题详情
试题详情
25. 浙江省宁波市2007―2008学年第一学期高三期末考试 试题详情
等差数列 的前n项和为Sn,且满足 的前n项和为Sn,且满足 数列 数列 试题详情
试题详情
(1)求数列 , , 的通项公式; 的通项公式; 试题详情
(2)记 中的最大项。 中的最大项。 试题详情
(1)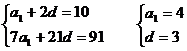 试题详情
 ……………………4分 ……………………4分
试题详情
试题详情
试题详情
试题详情
n=1时,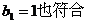 试题详情
∴ ………………9分 ………………9分 试题详情
(2)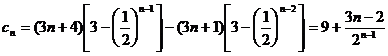 试题详情
 ……………………12分 ……………………12分
试题详情
当n=1时,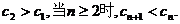 试题详情
当n=2时, 的最大值为11……………………14分 的最大值为11……………………14分 试题详情
26. 上海市嘉定一中2007学年第一学期高三年级测试(二) 试题详情
数列 中, 中, 。 。 试题详情
(1)求数列 的通项; 的通项; 试题详情
(2) ,求Sn。 ,求Sn。 试题详情
(1)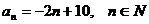 试题详情
(2)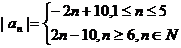 试题详情
10 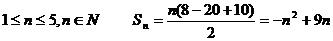 试题详情
20  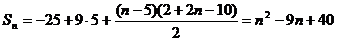 试题详情
由10,20可得 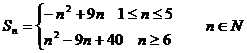 试题详情
27. 上海市嘉定一中2007学年第一学期高三年级测试(二) 试题详情
已知点 顺次为直线 顺次为直线 上的 上的 试题详情
点,点 顺次为x轴上的点,其中 顺次为x轴上的点,其中 对于任意自然数n,点An,Bn,An+1构成以Bn为顶点的等腰三角形。 对于任意自然数n,点An,Bn,An+1构成以Bn为顶点的等腰三角形。
(1)求数列{yn}的通项公式,并证明它为等差数列; 试题详情
(2)求证: 是常数,并求数列 是常数,并求数列 的通项公式; 的通项公式; 试题详情
(3)上述等腰△ 中是否可能存在直角三角形,若可能,求出此时a的值;若 中是否可能存在直角三角形,若可能,求出此时a的值;若 不可能,请说明理由。 试题详情
(1) 为定值 为定值 试题详情
(2)由题意得 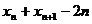 试题详情
试题详情
∴ 成等差数列 成等差数列 试题详情
 成等差数列 成等差数列
试题详情
试题详情
试题详情
试题详情
(3)当n为奇数时,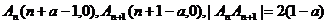 试题详情
当n为偶数时,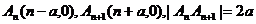 试题详情
作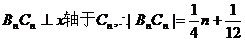 试题详情
要使等腰三角形为直角三角形,则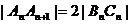 试题详情
10 n为奇数,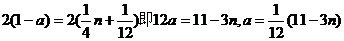 试题详情
当 ,无解 ,无解 试题详情
20 n为偶数,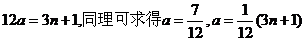 试题详情
综上  时,存在直角三角形 时,存在直角三角形 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(1)由题意知, 试题详情
试题详情
第一个图形的边数为3,从第二个图形起,每一个图形的边数均为上一个图形边数的4倍,所以第n个图形的边数为 . . 试题详情
因此 试题详情
(2) 试题详情
 , ,
试题详情
叠加得,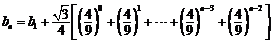 试题详情
试题详情
30. 2008年天津市十二区县重点学校高三毕业班联考(一) 试题详情
数列 满足 满足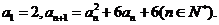 试题详情
(Ⅰ) 设 ,求证 ,求证 是等比数列; 是等比数列; 试题详情
(Ⅱ) 求数列 的通项公式; 的通项公式; 试题详情
试题详情
试题详情
 ,即 ,即  , …………3分 , …………3分
试题详情
 是以2为公比的等比数列 …………4分 是以2为公比的等比数列 …………4分
试题详情
(Ⅱ) 又 …………5分 …………5分 试题详情
 即 即  , …………7分 , …………7分
试题详情
 …………8分 …………8分 试题详情
故 …………9分 …………9分 试题详情
(Ⅲ) …………10分 …………10分 试题详情
 …………12分 …………12分
试题详情
又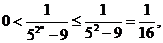  …………14分 …………14分 试题详情
31. 已知函数 的图象过原点,且关于点(-1,1)成中心对称. 的图象过原点,且关于点(-1,1)成中心对称. 试题详情
(Ⅰ)求函数 的解析式; 的解析式; 试题详情
试题详情
试题详情
解(Ⅰ) 因为函数 的图象过原点,即 的图象过原点,即 ,所以c =0, ,所以c =0, 试题详情
即 .又函数 .又函数 的图象关于点(-1,1)成中心对称, 的图象关于点(-1,1)成中心对称, 试题详情
所以 , ,  试题详情
(Ⅱ)由题意 ,开方取正得: ,开方取正得: , , 试题详情
即 = +1,所以 - =1.
∴数列{}是以1为首项,1为公差的等差数列. ∴ =1+(n-1)=n,即 = ,∴an= .
(Ⅲ)当n≥2时,an= < = - . 试题详情
所以 ,故 ,故 2 2
试题详情
32. 广东省梅州揭阳两市四校2008届高三第三次联考数学理科试卷 试题详情
已知 (m为常数,m>0且 (m为常数,m>0且 ) ) 试题详情
设 是首项为4,公差为2的等差数列. 是首项为4,公差为2的等差数列. (Ⅰ)求证:数列{an}是等比数列; 试题详情
(Ⅱ)若bn=an? ,且数列{bn}的前n项和Sn,当 ,且数列{bn}的前n项和Sn,当 时,求Sn; 时,求Sn; 试题详情
(Ⅲ)若cn= ,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,说明理由. ,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,说明理由. 试题详情
解:(Ⅰ)由题意 即 即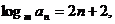 试题详情
∴
试题详情
∴ ∵m>0且
∵m>0且 ,∴m2为非零常数, ,∴m2为非零常数, ∴数列{an}是以m4为首项,m2为公比的等比数列
试题详情
(Ⅱ)由题意 , , 试题详情
当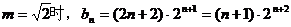 试题详情
∴ ① ①
①式两端同乘以2,得 试题详情
 ② ②
②-①并整理,得 试题详情
试题详情
试题详情
= 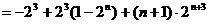 试题详情
试题详情
(Ⅲ)由题意 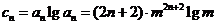 试题详情
要使 对一切 对一切 成立, 成立, 试题详情
即  对一切 对一切  成立, 成立, 试题详情
①当m>1时,  成立;
…………12分 成立;
…………12分 试题详情
②当0<m<1时,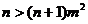 试题详情
试题详情
解得  , 考虑到0<m<1, ∴0<m< , 考虑到0<m<1, ∴0<m< 试题详情
综上,当0<m< 或m>1时,数列{cn }中每一项恒小于它后面的项. ----------14分 或m>1时,数列{cn }中每一项恒小于它后面的项. ----------14分 试题详情
33. 广东省梅州揭阳两市四校2008届高三第三次联考数学文科试题 试题详情
试题详情
试题详情
(1)求证:数列 是等差数列; 是等差数列; 试题详情
(2)求数列 中的最大项与最小项,并说明理由. 中的最大项与最小项,并说明理由. 试题详情
解:(1) , - --------4分 , - --------4分 试题详情
而 , , 试题详情
∴ . . -------------------------6分 -------------------------6分 试题详情
∴{ }是首项为 }是首项为 ,公差为1的等差数列.----------8分 ,公差为1的等差数列.----------8分 试题详情
(2)依题意有 ,而 ,而 , ------------10分 , ------------10分 试题详情
∴ . .
试题详情
函数 ,在(3.5, ,在(3.5, )上为减函数.在( )上为减函数.在( ,3.5)上也为减函数. ,3.5)上也为减函数. --------------12分 试题详情
故当n=4时, 取最大值3,n=3时,取最小值-1. ---------14分 取最大值3,n=3时,取最小值-1. ---------14分 试题详情
试题详情
试题详情
(2)写出 的逆序数an 的逆序数an 试题详情
(3)令 . . 试题详情
解:(1) …………4分 …………4分 试题详情
(2)n+2个数中任取两个数比较大小,共有 个大小关系 个大小关系 试题详情
 …………8分 …………8分 试题详情
(3)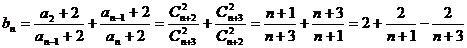 试题详情
试题详情
试题详情
 …………14分 …………14分 试题详情
试题详情
试题详情
(1)证明数列 是等比数列,并求数列 是等比数列,并求数列 的通项公式; 的通项公式; 试题详情
(2)记 ,当t=2时,数列 ,当t=2时,数列 的前n项和为Sn,求使Sn>2008的n的最小值; 的前n项和为Sn,求使Sn>2008的n的最小值; 试题详情
(3)当t=2时,是否存在指数函数g(x),使得对于任意的正整数n有 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由. 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由. 试题详情
(1) . . 试题详情
由题意 ,即 ,即 . …………1分 . …………1分 试题详情
∴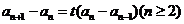 试题详情
试题详情
试题详情
以上各式两边分别相加得 ,∴ ,∴ , , 试题详情
当 时,上式也成立,∴ 时,上式也成立,∴ …………5分 …………5分 试题详情
(2)当t=2时,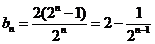 试题详情
试题详情
 …………7分 …………7分
试题详情
由 ,得 ,得 , , 试题详情
 , …………8分 , …………8分
试题详情
当 , , 试题详情
试题详情
(3)∵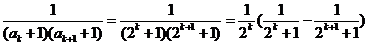 试题详情
令 ,则有: ,则有: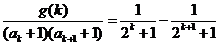 试题详情
则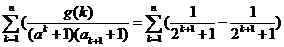 试题详情
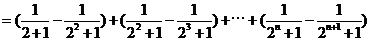 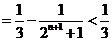
…………13分 试题详情
即函数 满足条件. 满足条件. 试题详情
试题详情
已知二次函数 满足条件: 满足条件: 试题详情
①0,1是 的两个零点;② 的两个零点;② 试题详情
(I)求函数 的解析式; 的解析式;
(II)设数列 试题详情
 ; ; 试题详情
(III)在(II)的条件下,当 的等差中项,试问数列 的等差中项,试问数列 中第几项的值最小?并求出这个最小值。 中第几项的值最小?并求出这个最小值。 试题详情
解:(I)由题意知: …………2分 …………2分 试题详情
解得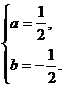 试题详情
故 …………4分 …………4分 试题详情
(II) , , 试题详情
当 , …………6分 , …………6分 试题详情
 …………8分 …………8分
试题详情
试题详情
故数列 …………10分 …………10分 试题详情
(III)若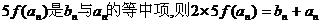 试题详情
从而 , , 试题详情
得 …………11分 …………11分 试题详情
试题详情
即数列 …………13分 …………13分 试题详情
且 …………14分 …………14分 试题详情
37. 江苏省如皋中学2007―2008学年度第二学期阶段考试高三数学(理科) 已知正项数列{ an }满足Sn+Sn-1=ta+2 (n≥2,t>0),a1=1,其中Sn是数列{ an }的前n项和. (Ⅰ)求通项an; 试题详情
(Ⅱ)记数列{}的前n项和为Tn,若Tn<2对所有的n∈N*都成立.求证:0<t≤1. 解:∵a1=1 由S2+S1=ta+2,得a2 =ta,∴a2 =0(舍)或a2=, Sn+Sn-1=ta+2
① Sn-1+Sn-2=ta+2 (n≥3)
② ①-②得an+an-1=t(a -a)(n≥3),(an+an-1)[1-t(an-an-1)] =0, 由数列{ an }为正项数列,∴an+an-1≠0,故an-an-1=(n≥3), 即数列{ an }从第二项开始是公差为的等差数列. ∴an= (2)∵T1=1<2,当n≥2时,Tn=t++++ …+=t+ t2(1-) =t+ t2 试题详情
要使Tn<2,对所有的n∈N*恒成立,只要Tn=t+ t2 < t+ t2≤2成立,∴0<t≤1. 试题详情
38. 在数列 中,a1=1,an+1=an+c (c为常数,n∈N*),且a1,a2,a5成公比不等于1的等比数列. 中,a1=1,an+1=an+c (c为常数,n∈N*),且a1,a2,a5成公比不等于1的等比数列. (Ⅰ) 求c的值; 试题详情
(Ⅱ) 设bn= ,求数列 ,求数列 的前n项和Sn . 的前n项和Sn . (本小题主要考查等差数列、等比数列、数列求和等基础知识;考查化归与转化的思想方法:考查推理与运算能力.) 解:(Ⅰ)∵an+1=an+c,a1=1,c为常数, ∴an=1+(n-1)c. ∴a2=1+c,a5=1+4c. 又a1,a2,a5成等比数列, 试题详情
∴(1+c)2=1+4c,解得c=0或c=2当c=0,an+1=an不合题意,舍去. ∴c=2. (Ⅱ)由(Ⅰ)知,an=2n-1, 试题详情
∴ ,∴Sn=b1+b2+…+bn ,∴Sn=b1+b2+…+bn 试题详情
= 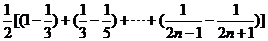 试题详情
=  = =  . . 试题详情
39. 江苏省滨海县08届高三第三次联考数学试卷2008-1-4 试题详情
试题详情
试题详情
试题详情
试题详情
解:(1)依题意, , , 试题详情
即 , , 试题详情
即 ; ; 试题详情
等号成立的条件为 ,即 ,即 , , 试题详情
试题详情
试题详情
则 ,得 ,得 试题详情
 , , , , 试题详情
则 , , ; ; 试题详情
(3)在(2)的条件下, , , , , 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(1)求数列 的通项公式; 的通项公式; 试题详情
(2) 当 时,试证明 时,试证明 ; ; 试题详情
试题详情
解:(1)当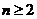 时 时 试题详情
 , ,
试题详情
试题详情
试题详情
试题详情
∴ --------4分 --------4分 试题详情
(2) 由(1)知当 时, 时, -----5分 -----5分 试题详情
 ,∴ ,∴ ----------------------------6分 ----------------------------6分
试题详情
即 ---------------------------------------7分 ---------------------------------------7分 试题详情
(3)∵ 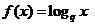 试题详情
 = =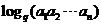 试题详情
= -----------------------9分 -----------------------9分 试题详情
∵ ---------------------------10分 ---------------------------10分 试题详情
试题详情
试题详情
试题详情
∵ 是正整数,∴ 是正整数,∴ 的值为1,2,3。 的值为1,2,3。 试题详情
试题详情
试题详情
(1)求 的值; 的值; 试题详情
试题详情
试题详情
又 ,且 ,且 不共线, 不共线, 试题详情
由平面向量基本定理,知:
试题详情
(2) 由 试题详情
试题详情
若 ,则 ,则 , , 试题详情
试题详情
若 ,则 ,则 为常数列, 为常数列, 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
令 ,则 ,则 , ,
试题详情
于是, 有唯一解 有唯一解 , ,
试题详情
试题详情
∴当对于给定的 ,都能找到唯一的一个 ,都能找到唯一的一个 , , 试题详情
试题详情
试题详情
试题详情
(Ⅱ)求数列 的前2n项和 的前2n项和 . . 试题详情
解:(I)解:方程 的两个根为 的两个根为 . . 试题详情
当k=1时, ,所以 ,所以 ; ; 试题详情
当k=2时, ,所以 ,所以 ; ; 试题详情
当k=3时, ,所以 ,所以 ; ; 试题详情
当k=4时, ,所以 ,所以 ; ; 试题详情
因为n≥4时, ,所以 ,所以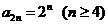 试题详情
(Ⅱ) = = . . 试题详情
43. 数列{an}的前n项和记为Sn,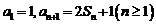 (I)求{an}的通项公式; 试题详情
(II)等差数列{bn}的各项为正,其前n项和为Tn,且 ,又 ,又 成等比数列,求Tn 成等比数列,求Tn 试题详情
(I)由 可得 可得 ,
……1分 ,
……1分 试题详情
两式相减得 ………3分
………3分 试题详情
又 ∴ ∴ ,故{an}是首项为1,公比为3得等比数列 4分 ,故{an}是首项为1,公比为3得等比数列 4分 试题详情
∴ .
……………………………6分 .
……………………………6分 试题详情
试题详情
故可设 …9分
…9分 试题详情
又 由题意可得 由题意可得 试题详情
 解得 解得 ……………11分
……………11分
试题详情
∵等差数列{bn}的各项为正,∴ ,∴ ,∴ ………………12分 ………………12分 试题详情
∴ …………………………………14分
…………………………………14分 试题详情
44. 已知数列{an}的前n项为和Sn,点 在直线 在直线 上. 上. 试题详情
数列{bn}满足 ,前9项和为153. ,前9项和为153. (Ⅰ)求数列{an}、{bn}的通项公式; 试题详情
试题详情
(Ⅲ)设 ,问是否存在 ,问是否存在 ,使得 ,使得 成立? 成立? 若存在,求出m的值;若不存在,请说明理由. 试题详情
解:(Ⅰ)由题意,得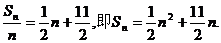 试题详情
故当 时, 时,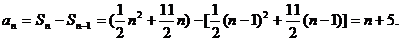 试题详情
当n = 1时, ,而当n =
1时,n + 5 = 6, ,而当n =
1时,n + 5 = 6, 试题详情
所以, …………………………………………………… 2分 …………………………………………………… 2分 试题详情
又 , , 试题详情
所以{bn}为等差数列,于是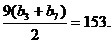 试题详情
而 试题详情
因此, ………………4分 ………………4分 试题详情
(Ⅱ) 试题详情
 …………………………6分 …………………………6分
所以, 试题详情
试题详情
 …………………………7分 …………………………7分 试题详情
由于 , , 试题详情
因此Tn单调递增,故 ………………………………………………8分 ………………………………………………8分 试题详情
令 …………………………………………9分 …………………………………………9分 试题详情
(Ⅲ)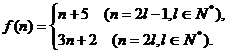 ①当m为奇数时,m + 15为偶数. 试题详情
此时 , , 试题详情
所以 ………………………………………………11分 ………………………………………………11分 ②当m为偶数时,m + 15为奇数. 试题详情
此时 , , 试题详情
所以 (舍去). ……………………13分 (舍去). ……………………13分 试题详情
综上,存在唯一正整数m =11,使得 成立. ……………………14分 成立. ……………………14分 试题详情
试题详情
(1)求 的值. 的值. 试题详情
试题详情
(3)若自然数 ( ( 为正整数) 为正整数) 试题详情
试题详情
试题详情
(理科考生做)求 的所有可能值. 的所有可能值. 试题详情
试题详情
则 ……………………3分 ……………………3分 试题详情
试题详情
则 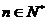 …………5分 …………5分 试题详情
又  则 36=3am, 则 36=3am, …………8分 …………8分 试题详情
试题详情
则 ……10分 ……10分 试题详情
试题详情
又因为  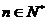
……………………16分 试题详情
试题详情
试题详情
∴ …………14分 …………14分 试题详情
又∵ 成等比数列, ∴ 成等比数列, ∴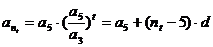 试题详情
∴ {6,7,8,9,10,…}对一切 {6,7,8,9,10,…}对一切 成立, 成立, 试题详情
试题详情
∴ ,(由二项式定理知, ,(由二项式定理知, 试题详情
 恒成立) ∴ 恒成立) ∴ ( ( {2,3,4,5,…}) {2,3,4,5,…})
(注的证明可用无穷递降法完成,证略. ) ………………16分 试题详情
46. 设正项数列{ }的前项和为Sn,q为非零常数。已知对任意正整数n, m,当n > m时, }的前项和为Sn,q为非零常数。已知对任意正整数n, m,当n > m时, 总成立。 总成立。 试题详情
1)求证数列{ }是等比数列; }是等比数列; 试题详情
试题详情
解: 1)因为对任意正整数n, m,当n > m时, 总成立。 总成立。 试题详情
试题详情
试题详情
2)若 ,则 ,则 。所以 。所以 试题详情
 ≥ ≥ 。
…7分 。
…7分
试题详情
试题详情
所以 ≥ ≥ 。
…10分 。
…10分 试题详情
又因为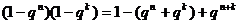 试题详情
≤ 。所以 。所以 试题详情
试题详情
试题详情
当且仅当 时取“=”。
…13分 时取“=”。
…13分 试题详情
47. 设不等式组 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*). 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*). (1)求f(1)、f(2)的值及f(n)的表达式;(可以不作证明) 试题详情
(2)记 ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值 ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值 范围. (1)f(1)=3………………………………………………………………………………(1分)
f(2)=6………………………………………………………………………………(2分) 当x=1时,y=2n,可取格点2n个;当x=2时,y=n,可取格点n个 ∴f(n)=3n…………………………………………………………………………(4分) 试题详情
(2) ………………………………………………(9分) ………………………………………………(9分) 试题详情
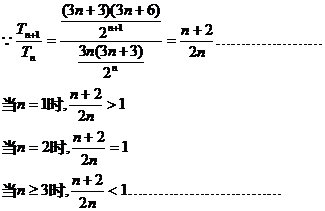 ∴T1<T2=T3>T4>…>Tn 试题详情
故Tn的最大值是T2=T3=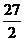 试题详情
∴m≥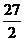 ………………………………………………………………() ………………………………………………………………() 试题详情
试题详情
试题详情
(1)求函数 解析式; 解析式; (2)求数列{an}、{bn}的通项公式; 试题详情
(3)若对任意实数 ,总存在自然数k,当n≥k时, ,总存在自然数k,当n≥k时, 恒成立,求k的最小值。 恒成立,求k的最小值。 试题详情
试题详情
(2)∵ ,∴ ,∴ , , 试题详情
试题详情
又  , , 试题详情
相加有 ,∴ ,∴ ……9分 ……9分 试题详情
(3)对任意实数λ∈[0,1]时, 恒成立, 恒成立, 试题详情
试题详情
设 , ……10分 , ……10分 试题详情
∴ , ……11分 , ……11分 试题详情
试题详情
试题详情
(Ⅰ)求 的通项公式; 的通项公式; 试题详情
试题详情
解:(Ⅰ)依题意,得 .于是,当 .于是,当 时,有 时,有 试题详情
 . .
试题详情
两式相减,得 ( ( ). ). 试题详情
试题详情
因此, ( ( ); ); 试题详情
(Ⅱ)因为 ,所以 ,所以 试题详情
 . .
试题详情
试题详情
试题详情
试题详情
(Ⅱ)若 ,数列 ,数列 中是否存在最大项与最小项,若存在,求出最大项与最小项,若不存在,说明理由; 中是否存在最大项与最小项,若存在,求出最大项与最小项,若不存在,说明理由; 试题详情
(Ⅲ)若 ,试证明: ,试证明: . . 试题详情
解  ,则 ,则 (n≥2,nÎN*). (n≥2,nÎN*). 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(Ⅲ)先用数学归纳法证明 ,再证明 ,再证明 . . 试题详情
①当n=1时, 成立, 成立, 试题详情
②假设n=k时命题成立,即 , , 试题详情
试题详情
综合①②有,命题对任意nÎN*时成立,即 .下证 .下证 . . 试题详情
∵ ,∴ ,∴ .综上所述: .综上所述: . . 【总结点评】本题集数列、向量、函数、导数、不等式于一体,充分展示了《考试大纲》“构造有一定深度和广度的数学问题,要注重问题的多样化,体现思维的发散性”的题目,这需要我们加强这一方面的训练,需要从多层次、多角度去思考问题. 试题详情
试题详情
(Ⅰ)求数列 的通项公式; 的通项公式; 试题详情
试题详情
试题详情
试题详情
当 时, 时, ; ; 试题详情
试题详情
故 . . 试题详情
(Ⅱ)由 求导可得, 求导可得,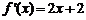 试题详情
试题详情
又∵ ,∴ ,∴ . . 试题详情
∴ 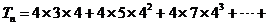  ………① ………① 试题详情
由① 可得: 可得: 试题详情
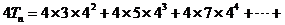  ………② ………②
试题详情
①-②可得: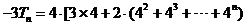 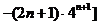 试题详情
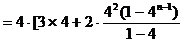  . .
试题详情
∴ . . 试题详情
(Ⅲ)∵ , ,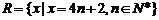 试题详情
试题详情
试题详情
又∵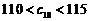 试题详情
∴ 解得 解得 . . 【总结点评】强调在“知识的交汇处”命制试题,是近年高考命题的趋势,本题集函数、导数、数列、不等式于一体,体现了知识间的交汇与融合,同时又考查了数列的基本解题方法,考查了学生分析问题和解决问题. 试题详情
试题详情
试题详情
试题详情
(Ⅱ)求 ; ; 试题详情
试题详情
解:(Ⅰ)当 时, 时, , , 试题详情
得 . . 试题详情
∴数列 是以 是以 为首项,4为公差的等差数列. 为首项,4为公差的等差数列. 试题详情
∴
试题详情
 . .
试题详情
(Ⅱ) 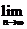 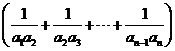 试题详情
=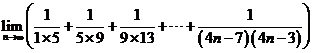 试题详情
=
试题详情
= = = . . 试题详情
(Ⅲ)由 得: 得:  , , 试题详情
∴ . .
试题详情
试题详情
试题详情
(1)求数列 的通项公式; 的通项公式; 试题详情
试题详情
(3)当 最大时,求 最大时,求 的值. 的值. 试题详情
解:(1) , , , , 试题详情
又 ………………2分 ………………2分 试题详情
试题详情
而 , , ……………………4分 ……………………4分 试题详情
 , , ……………………5分 ……………………5分
试题详情
(2) …………………6分 …………………6分 试题详情
试题详情
试题详情
 ……………………9分
……………………9分
试题详情
(3)由 得 ……………………10分 得 ……………………10分 试题详情
试题详情
试题详情
试题详情
(1)求函数 的表达式; 的表达式; 试题详情
试题详情
试题详情
解(1)∵不等式 ≤0的解集有且只有一个元素 ≤0的解集有且只有一个元素 试题详情
试题详情
试题详情
当 时函数 时函数 在(0,2)上递减,满足条件② 在(0,2)上递减,满足条件② 试题详情
综上得 ,即 ,即 ------------------------------4分 ------------------------------4分 试题详情
(2)由(1)知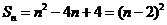 试题详情
当 时, 时,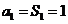 试题详情
试题详情
∴ -------------------------------------------6分 -------------------------------------------6分 试题详情
由题设可得 ---------------------------------------7分 ---------------------------------------7分 试题详情
试题详情
试题详情
即当 ≥3时,数列{ ≥3时,数列{ }递增, }递增, 试题详情
试题详情
∴数列{ }的变号数为3。--------------------------------------9分 }的变号数为3。--------------------------------------9分 试题详情
(3)∵ = = , 由(2)可得: , 由(2)可得: 试题详情
 --------------11分 --------------11分
试题详情
=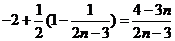 = = ---13分 ---13分 试题详情
试题详情
∴数列{ }存在最小项 }存在最小项 -----------------------------14分 -----------------------------14分 试题详情
〔或∵ = = ,由(2)可得: ,由(2)可得: 试题详情
 --------------11分 --------------11分
试题详情
=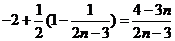 试题详情
试题详情
试题详情
∴当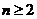 时, 时, 最小,--------13分 最小,--------13分 试题详情
试题详情
试题详情
(1)求函数 的表达式; 的表达式; 试题详情
(2) 求数列{ }的通项公式; }的通项公式; 试题详情
试题详情
解(1)∵不等式 ≤0的解集有且只有一个元素 ≤0的解集有且只有一个元素 试题详情
试题详情
试题详情
当 时函数 时函数 在(0,2)上递减,满足条件② 在(0,2)上递减,满足条件② 试题详情
综上得 ,即 ,即 ---------------------5分 ---------------------5分 试题详情
(2)由(1)知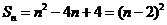 试题详情
当 时, 时,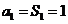 试题详情
试题详情
∴ --------------------------------------------9分 --------------------------------------------9分 试题详情
(3)由题设可得 ----------------------------11分 ----------------------------11分 试题详情
试题详情
试题详情
即当 ≥3时,数列{ ≥3时,数列{ }递增, }递增, 试题详情
试题详情
∴数列{ }的变号数为3.----------------------------------------14分 }的变号数为3.----------------------------------------14分 试题详情
试题详情
(Ⅰ)求数列 的通项公式; 的通项公式; 试题详情
(Ⅱ)求证: ; ; 试题详情
(Ⅲ)求证:当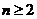 时, 时, . . 试题详情
试题详情
试题详情
试题详情
(2) , ,  , , 试题详情
 , , 试题详情
 , ,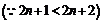 试题详情
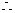  .
…………………(8分) .
…………………(8分)
试题详情
(3)∵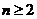 试题详情
试题详情
由(2)知 , , , , 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
解:(1)依题意, , , 试题详情
即 ,--------------3分 ,--------------3分 试题详情
即 ; ; 试题详情
等号成立的条件为 ,即 ,即 , , 试题详情
试题详情
试题详情
则 ,得 ,得 --------------------------------8分 --------------------------------8分 试题详情
 , , , , 试题详情
则 , , ;------------------10分 ;------------------10分 试题详情
(3)在(2)的条件下, , , , , 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
58. 无穷数列 满足: 满足: , , 试题详情
 , , . .
试题详情
(1)求证: ; ; 试题详情
(2)求证: . . 试题详情
【证明】(1)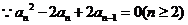  , , 试题详情
则 , , ,…………………………2分 ,…………………………2分 试题详情
试题详情
试题详情
试题详情
 ……………………………………7分 ……………………………………7分
试题详情
(2) 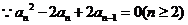 , , , , 试题详情
则 , , ,…………10分 ,…………10分 试题详情
试题详情
 ,……… 12分 ,……… 12分
试题详情
试题详情
则 , , 试题详情
即 .………………… 15分 .………………… 15分 试题详情
57. 定义F(x,y)= yx (x>0,y>0). 试题详情
(Ⅰ)设函数f(n)=  (n∈N*),求函数f(n)的最小值; (n∈N*),求函数f(n)的最小值; (Ⅱ)解关于x的不等式F(2,x ?a -1)≤(a -1)2; 试题详情
(Ⅲ)设g(x)=F(x,2),正项数列{an}满足:a1=3,g(a n+1)=  ,求数列{ an} ,求数列{ an} 的通项公式,并求所有可能的乘积aiaj(1≤i≤j≤n)的和. 本小题主要考查函数、数列、不等式等基础知识,考查应用数学知识分析问题和解决问题的能力,考查分类讨论等数学思想方法.满分14分. 试题详情
解法一:(Ⅰ)f(n)=  , ,  ...............2分 ...............2分 因为2n2-(n+1)2=(n-1)2-2, 当n≥3时,(n-1)2-2>0,所以当n≥3时f(n+1)>f(n); 当,n<3时,(n-1)2-2<O,所以当n<3时f(n+1)<f(n). 试题详情
所以当n=3时f(n)取到最小值为f(3)= .........................4分 .........................4分 试题详情
(Ⅱ)原不等式等价于不等式组 即 即 5分 5分 (i)当a>1时,2<a+1<2a,原不等式的解集是{x|a+1<x≤2a}.…………6分 试题详情
(ii)当a=l时,2a=a+1=2,原不等式的解集是空集 .…………………7分 .…………………7分 (iii)当a<1时,2a<a+1<2,原不等式的解集为{x|a+1<x≤2}.…………8分 试题详情
综上,a>1时,原不等式的解集是(a+1,2a];a=1时,原不等式的解集是 ; ; a<l时,原不等式的解集是(a+1,2].………………………………………9分 试题详情
(Ⅲ)因为g(x)=2x,所以g(an+1)=
 ,又g(an+1)= ,又g(an+1)=
 = =  , , 所以an+1=3an.又a1=3, 所以数列{an}是首项a1=3,公比为3的等比数列, 所以an=3?3 n-1=3 n. ………………………………………………………10分 试题详情
记数列{3 n}的所有可能的乘积 (1≤i≤j≤n)的和为S,则 (1≤i≤j≤n)的和为S,则 S=a1?a1+(a1+a2)
?a2+…+(a1+a2+…+an) ?an………………………………11分 = 3?31+(3+32) ?32+…+(3+32+…+3n) ?3n…………………………………12分 试题详情
= 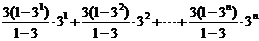 试题详情
=  + + 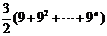 试题详情
= 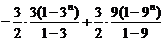 试题详情
=  ……………………………………………14分 ……………………………………………14分 试题详情
解法二:(Ⅰ)由f(n)=  ,计算得: ,计算得: 据此猜想n=3时,f(n)取到最小值.………………………………………2分 以下用数学归纳法证明n≥5时,n2<2 n成立. (i)当n=5时,52<2 5,不等式成立. (ii)假设n=k(k≥5)时不等式成立,即k2>2 k 那么2k+1=2 k ?2>k2 ?2 , 试题详情
因为k≥5,所以2k2-(k+1)2=k2-2k-1=(k-1)2-2>0. 所以2k+1>(k+1)2.即当n=k+1时,不等式也成立. 根据(i)和(ii)所述,对于所有n≥5,n∈N *,n2<2 n都成立. 试题详情
结合上表可知猜想正确,即当n=3时f(n)取到最小值为f(3)= .………4分 .………4分 (Ⅱ)同解法一. (Ⅲ)同解法一,得an=3n.………………………………………………………10分
由ai?aj=3i?3j=3i+j (1≤i≤j≤n),列表如下: 试题详情
试题详情
记数列{3n}的所有可能的乘积 (1≤i≤j≤n)的和为S,将这个“上三角形”表绕“对角线”对称地填在“下三角形”中,得到正方形数表: (1≤i≤j≤n)的和为S,将这个“上三角形”表绕“对角线”对称地填在“下三角形”中,得到正方形数表: 试题详情
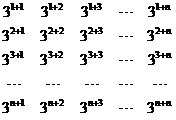
记第一行的和为S1,那么2S一(32+34+36+…+32n)=S1(1+3+32+…+3n-1). 试题详情
所以2S = (3 n-1)(1+3+32+…+3 n-1)+ (3 n-1)(1+3+32+…+3 n-1)+ (9 n -1), (9 n -1), 试题详情
所以S =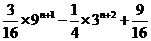 试题详情
解法三:(Ⅰ)因为f(n)=  ,设 ,设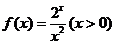 试题详情
由 , , 试题详情
试题详情
试题详情
所以f(n)=  的最小值只可能在n=2或n=3处取到, 的最小值只可能在n=2或n=3处取到, 试题详情
注意到f(2)=1,f(3)= ,所以当n=3时,f(n)取到最小值为 f(3)= ,所以当n=3时,f(n)取到最小值为 f(3)= . . (Ⅱ)、(Ⅲ)同解法一. 解法四:(Ⅰ)同解法二,猜想n=3时, f(n)取到最小值.………………………………2分 证明如下:当n≥5时, 试题详情
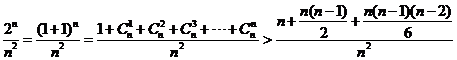
因为n≥5时,n-2≥3, 试题详情
所以 ≥ ≥ =1. =1. 试题详情
结合上表可知猜想正确,即当n=3时,f(n)取到最小值为f(3)=  . . (Ⅱ)(Ⅲ)同解法一. 试题详情
58. 在长、株、潭三市获国务院批准的“两型城市后”后,省政府决定关闭一批高能耗、高污染的中小型企业,并制定对企业的转岗员工的经济补助方案如下:第一年到政府社保部门领取关闭前工资的100%,从二年起,以后每年在社保部门按上一年补助金的 发放经济补助金.同时政府负责对企业进行调整改造,转型为转岗人员再就业的经济实体,经济实体第一年为投资阶段没有利润,第二年每人可获得利润分红收入b元,根据市场预测,从第三年起利润分红收入可以在上一年的基础上增加50%.如果某员工转岗前的工资收入为a元,转岗后第n年的收入为an元. 发放经济补助金.同时政府负责对企业进行调整改造,转型为转岗人员再就业的经济实体,经济实体第一年为投资阶段没有利润,第二年每人可获得利润分红收入b元,根据市场预测,从第三年起利润分红收入可以在上一年的基础上增加50%.如果某员工转岗前的工资收入为a元,转岗后第n年的收入为an元. (1)试用转岗后的年数n表示该员工的经济总收入an; 试题详情
(2)若b= 该员工哪年的总经济收入最少?并求最少收入; 该员工哪年的总经济收入最少?并求最少收入; 试题详情
(3)若b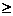  ,问是否一定可以保证该员工转岗一年后的总收入永远超过转岗前的收入?并说明理由. ,问是否一定可以保证该员工转岗一年后的总收入永远超过转岗前的收入?并说明理由. 试题详情
解(1)依题设,当n=1时,a1=a,当n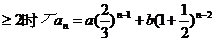 试题详情
 a (n=1)
a (n=1)
故an 试题详情
a? ( )n-1+b( )n-1+b( )n-2 (n≥2,n∈N*) )n-2 (n≥2,n∈N*)
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
综合上所述,当b≥ ,一定可以保证该员工转岗一年后的收入永远超过转岗前的收入。 ,一定可以保证该员工转岗一年后的收入永远超过转岗前的收入。 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(2)对于(1)中 ,不等式化为 ,不等式化为 ….. 3分 ….. 3分 试题详情
设 , , 试题详情
 , ,
试题详情
∴数列 单调递增,…………………….. 5分 单调递增,…………………….. 5分 试题详情
所以 ,要是不等式恒成立,只要 ,要是不等式恒成立,只要 ……………. 6分 ……………. 6分 试题详情
试题详情
试题详情
(3)设公共项 为正整数, 为正整数, 试题详情
当 为奇数时, 为奇数时, …………………….. 9分 …………………….. 9分 试题详情
试题详情
试题详情
当 为偶数时, 为偶数时, …………………….. 12分 …………………….. 12分 试题详情
试题详情
试题详情
60. 已知集合 表示和 表示和 试题详情
 中所有不同值的个数. 中所有不同值的个数.
试题详情
(I)已知集合 ; ; 试题详情
(II)若集合 ; ; 试题详情
(III)求 的最小值. 的最小值. (I)解:由2+4=6,2+6=8,2+8=10,4+6=10,4+8=12,6+8=14, 试题详情
得 , , 由2+4=6,2+8=10,2+16=18,4+8=12,4+16=20,8+16=24, 试题详情
得 …………4分 …………4分 试题详情
(II)证明:因为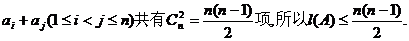 试题详情
试题详情
因此 …………9分 …………9分 试题详情
(III)解:不妨设 ,可得 ,可得 试题详情
试题详情
故对这样的集合 …………14分 …………14分 试题详情
| 
 是
是 的前
的前 项和,且有
项和,且有 ,则数列
,则数列 的通项
的通项 .
. ,
, 为正整数
为正整数 2、一次展览会上展出一套由宝石串联制成的工艺品,如图所示.若按照这种规律依次增加一定数量的宝石,则第
2、一次展览会上展出一套由宝石串联制成的工艺品,如图所示.若按照这种规律依次增加一定数量的宝石,则第 件工艺品所用的宝石数为 颗 (结果用
件工艺品所用的宝石数为 颗 (结果用 表示).
表示).