
桐梓一中2009届高三第三次月考试题
数学(理)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共分12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数f(x)=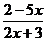 的值域是:
的值域是:
A.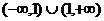 B.
B.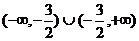 C.{y|y¹
C.{y|y¹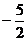 } D.{y|y¹0}
} D.{y|y¹0}
2.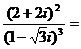
A. 1+i B. 1-i C. ? i D. i
3.在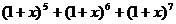 的展开式中,含
的展开式中,含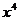 项的系数是首项为-2,公差为3的等差数列的( )
项的系数是首项为-2,公差为3的等差数列的( )
A.第13项 B.第18项 C.第11项 D.第20项
4.已知集合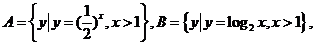 则
则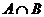 等于( )
等于( )
A .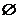 B.
B. 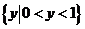 C .
C .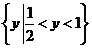 D.
D. 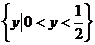
5. 在数列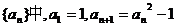 则此数列的前4项之和为 ( )
则此数列的前4项之和为 ( )
A.0
B.
 6.已知随机变量x的频率分布条形图如右图所示:
6.已知随机变量x的频率分布条形图如右图所示:
则它的数学期望是:
A.6.3 B.
7.有一块直角三角板ABC,∠A=30°,∠B=90°,BC边在桌面上,当三角板所在平面与桌面成45°角时,AB边与桌面所成的角等于 ( )
A.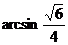 B.
B.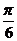 C.
C.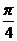 D.
D.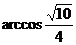
8.已知实系数的一元二次方程ax2+bx+c=0(a≠0),在下列结论中正确的为( )
A.Δ=b2
B.Δ=b2
C.Δ=b2
D.Δ=b2
9.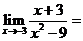 ( )
( )
A.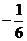 B。
B。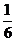 D。
D。
10. 过曲线y=x2+x-2上点P0的切线平行于直线y=3x-1,则点P0坐标为
A. (1,4) B. (0,2) C. (-2,0) D.(1,0)
11. 将函数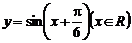 图象上所有点向左平行移动
图象上所有点向左平行移动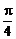 个单位长度,再把所得图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为
个单位长度,再把所得图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为
A.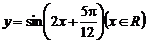 B.
B.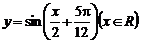
C.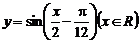 D.
D.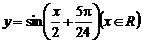
12.若方程 有正数解,则实数
有正数解,则实数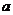 的取值范围是( )
的取值范围是( )
A.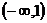 B.
B.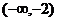 C.
C.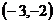 D.
D.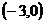
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在答题纸上。
13.椭圆5x2-ky2=5的一个焦点是(0,2),那么k=___________.
 14.函数
14.函数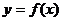 在定义域
在定义域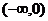 内存在反函数,且
内存在反函数,且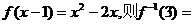

15.某航空公司规定,乘机所携带行李的重量(kg)与
其运费(元)由如图的一次函数图像确定,那么乘客免
费可携带行李的最大重量为 ___________。
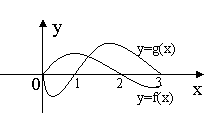 16.已知
16.已知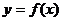 是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在
是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],且它们在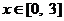 上的图象如图所示,则不等式
上的图象如图所示,则不等式
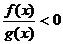 的解集是
。
的解集是
。
答题卷
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二.填空题:
13. 14. 15. 16.
三、解答题(本题17―20小题每题12分,21、22小题每题14分,共76分)
17.从汽车东站驾车至汽车西站的途中要经过8个交通岗,假设某辆汽车在各交通岗遇到红灯的事件是独立的,并且概率都是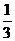 .求
.求
(1)这辆汽车首次遇到红灯前,已经过了两个交通岗的概率;
(2)这辆汽车在途中遇到红灯数ξ的期望与方差.
18.设f(x) = alnx + bx2 + x在x1=1与x2=2时取得极值,
(1)试确定a、b的值;
(2)求f(x)的单调增区间和减区间;
(3)判断f(x)在x1、x2处是取极大值还是极小值。
19.已知 是定义在R上的奇函数,当
是定义在R上的奇函数,当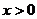 时,
时,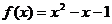 ,
,
(1)求函数 ;
;
(2)解不等式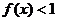 .
.
20.已知等差数列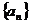 中,
中,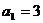 ,前n项和
,前n项和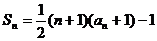 .
.
(Ⅰ)求数列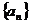 的公差d;
的公差d;
(Ⅱ)记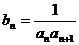 ,且数列
,且数列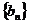 的前n项和为Tn,求
的前n项和为Tn,求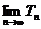
21、记函数f(x)=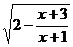 的定义域为A, g(x)=lg[(x-a-1)(
的定义域为A, g(x)=lg[(x-a-1)(
(1) 求A;
(2) 若B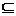 A, 求实数a的取值范围.
A, 求实数a的取值范围.
22.定义在定义域D内的函数y=f(x),若对任意的x1,x2ÎD都有|f(x1)-f(x2)|<1,则称函数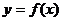 为“西湖函数”,否则称“非西湖函数”.函数
为“西湖函数”,否则称“非西湖函数”.函数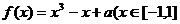 ,
,
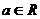 )是否为“西湖函数”?如果是,请给出证明;如果不是足,请说明理由.
)是否为“西湖函数”?如果是,请给出证明;如果不是足,请说明理由.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
D
D
A
A
C
C
A
D
B
D
二、填空题:(本题每小题4分,共16分)
13。-1 14、-2 15、{x|-2<x<-1或0<x<1或2<x<3} 16、
三、解答题:(本题共76分)
17.(1)∵这辆汽车在第一、二个交通岗均未遇到红灯,而第三个交通岗遇到红灯

(2) ∽
∽

18.解(1)令 则2bx2+x+a=0
则2bx2+x+a=0
由题意知:x=1,2是上方程两根,由韦达定理:
 ∴
∴
(2)由(1)知:
令 解得:x<0或1<x<2
解得:x<0或1<x<2
∴f(x)的单调增区间为(1,2) 减区间是(0,1)和(2,+ )
)
(3)由(2)知:f(x)在x1=1处取极小值,在x2=2处取极大值。
19.(1)


(2)
20、(Ⅰ)由已知
(Ⅱ)由(Ⅰ)得

21、解:(1)2- ≥0, 得
≥0, 得 ≥0, x<-1或x≥1 即A=(-∞,-1)∪[1,+
∞)
≥0, x<-1或x≥1 即A=(-∞,-1)∪[1,+
∞)
(2) 由(x-a-1)(
∵a<1,∴a+1> A, ∴
A, ∴ 或a≤-2, 而a<1,
或a≤-2, 而a<1,
∴ ≤a<1或a≤-2, 故当B
≤a<1或a≤-2, 故当B A时, 实数a的取值范围是(-∞,-2)∪[
A时, 实数a的取值范围是(-∞,-2)∪[ ,1]
,1]
22、因为 ,
,


 是“西湖函数”.
是“西湖函数”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com