
假期复习第一天――――――集合与简易逻辑
一.这几个概念你掌握了吗?请回顾一遍:
1.子集、空集的概念,集合中元素的3个性质,集合的3种表示方法;
2.交集、并集、全集、补集等概念。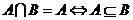 ,
,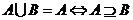
3. “或”“且”“非”的含义。四种命题及其互相关系。
4.充要条件关系怎么判定?
二.特别要注意下列方法:
1.解决集合问题,首先要弄清楚集合中的元素是什么;
2.弄清集合中元素的本质属性,能化简的要化简;
3.抓住集合中元素的3个性质,对互异性要注意检验;
4.正确进行“集合语言”和“数学语言”的相互转化.
5.求交集、并集、补集时充分发挥数轴或文氏图的作用;
6.含参数的问题,要有讨论的意识,分类讨论时要防止在空集上出问题;
7逻辑联结词“或”“且”“非”与集合中的并集、交集、补集有着密切的关系,解题时注意类比;
8.有时一个命题的叙述方式比较的简略,此时应先分清条件和结论,该写成“若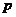 ,则
,则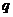 ”的形式
”的形式
9.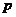 ,
,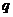 都假则“
都假则“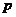 或
或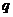 ”为假,其余“
”为假,其余“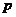 或
或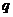 ”为真。
”为真。
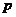 ,
,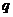 都真则“
都真则“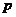 且
且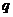 ”为真,其余“
”为真,其余“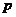 且
且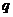 ”为假。
”为假。
三.下列习题你必须掌握:
1.已知集合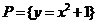 ,
,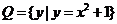 ,
,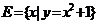 ,
,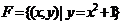 ,
,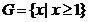 ,则
,则

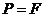
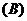
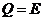
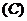
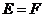
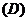
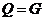
提示:弄清集合中的元素是什么,能化简的集合要化简.
2.设全集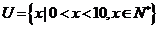 ,若
,若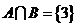 ,
,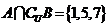 ,
,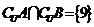 ,则A=
。
,则A=
。
提示:文氏图和数轴是处理集合运算的关键。
3.已知集合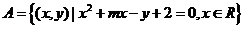 ,
,
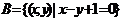 ,若
,若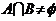 ,求实数
,求实数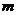 的取值范围.
的取值范围.
提示:首先要高清楚A,B的含义,还要抓住本题的几何背景,若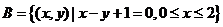 又怎么办?
又怎么办?
4.若集合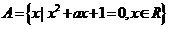 ,集合
,集合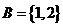 ,且
,且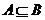 ,求实数
,求实数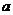 的取值范围.
的取值范围.
提示:要有讨论的意识,并注意空集的情况。
5.分别写出命题“若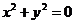 ,则
,则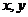 全为零”的逆命题、否命题和逆否命题.
全为零”的逆命题、否命题和逆否命题.
提示:写四种命题时应先分清题设和结论.
6.已知命题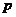 :方程
:方程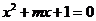 有两个不相等的实负根,命题
有两个不相等的实负根,命题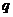 :方程
:方程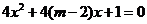 无实根;若
无实根;若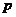 或
或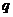 为真,
为真,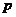 且
且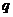 为假,求实数
为假,求实数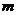 的取值范围.
的取值范围.
提示:先分别求满足条件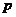 和
和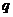 的
的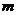 的取值范围,再利用复合命题的真假进行转化与讨论.
的取值范围,再利用复合命题的真假进行转化与讨论.
7.指出下列各组命题中,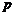 是
是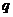 的什么条件?
的什么条件?
(1)在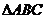 中,
中,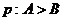 ,
,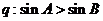
(2)对于实数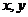 ,
,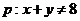 ,
,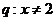 或
或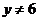
(3)在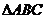 中,
中,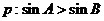 ,
,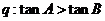
(4)已知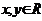 ,
,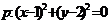 ,
,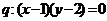 。
。
提示: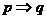 ,则
,则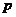 是
是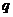 的充分条件,
的充分条件,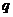 是
是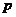 的必要条件,说明不充分或不必要时,常构造反例.
的必要条件,说明不充分或不必要时,常构造反例.
8.(1)是否存在实数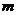 ,使得
,使得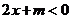 是
是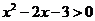 的充分条件?
的充分条件?
提示:对数集A,B,若A是B的充分条件,则AÍB。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com