1．数列通项公式的意义及求法，数列的表示方法。

2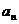．与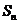的关系及应用：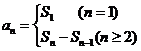

3．等差、等比数列的定义，通项公式和前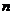项和的公式。

1．给出数列的前几项,求通项时,要对项的特征进行认真的分析、化归；

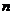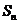2．数列前项的和和通项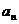是数列中两个重要的量，在运用它们的关系式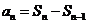时，一定要注意条件 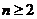，求通项时一定要验证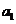是否适合．

3．涉及等差（比）数列的基本概念的问题，常用基本量来处理；

4．使用等比数列前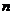项和公式时，必须弄清公比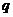是否可能等于1还是必不等于1，如果不能确定则需要讨论；

5．在求解数列问题时要注意运用函数思想，方程思想和整体消元思想，设而不求．

1．根据下面各个数列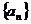的首项和递推关系，求其通项公式：

（1）；

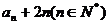（2）；

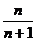
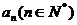（3）．

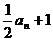
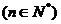提示：这三道题是递推数列的基本类型：它们都可以通过特定的方法转换为等差、等比数列的问题来解决。

1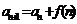．：叠加法；2。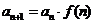：叠乘法；

（3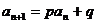）型：转换为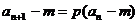来构造新数列（等比数列）。

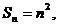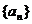2．若S_n是数列{a_n}的前n项和，且则是

A．等比，但不是等差数列  B．等差，但不是等比数列

C．等差，也是等比数列    D．既非等比又非等差数列

3．数列－1，，－，，…错误！未定义书签。的一个通项公式是 

A．a_n＝(－1)ⁿ              B．a_n＝(－1)ⁿ

C．a_n＝(－1)ⁿ     D．a_n＝(－1)ⁿ

4．设数列{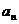}的前n项和为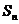，且，．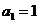

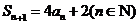（1）设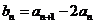，求证：数列{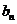}是等比数列；

（2）设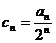，求证：数列{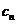}是等差数列；

5．正数数列{a_n}的前n项和为S_n，且2．

(1)    试求数列{a_n}的通项公式；

(2)设b_n＝，{b_n}的前n项和为T_n，求证：T_n<．