
假期复习第九天―――等差、等比数列的性质,数列求和
一.这几个性质你掌握了吗?请回顾一遍:
1.等差数列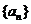 的任意连续
的任意连续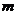 项的和构成的数列
项的和构成的数列 仍为等差数列.
仍为等差数列.
2.等差数列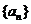 中,若
中,若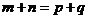 ,则
,则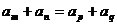
3.等比数列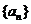 中,若
中,若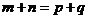 ,则
,则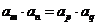
4.等比数列{an}的任意连续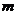 项的和构成的数列
项的和构成的数列 仍为等比数列.
仍为等比数列.
5.两个等差数列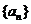 与
与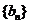 的和差的数列
的和差的数列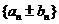 仍为等差数列.
仍为等差数列.
6.两个等比数列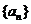 与
与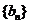 的积、商、倒数的数列
的积、商、倒数的数列 、
、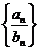 、
、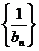 仍为等比数列.
仍为等比数列.
7.运用倒序相加、错位相减、拆项相消等重要的数学方法进行求和运算。
二.特别要注意下列方法:
1.解决等差数列和等比数列的问题时,通常考虑两类方法:①基本量法:即运用条件转化为关于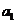 和
和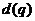 的方程;②巧妙运用等差数列和等比数列的性质,一般地运用性质可以化繁为简,减少运算量.
的方程;②巧妙运用等差数列和等比数列的性质,一般地运用性质可以化繁为简,减少运算量.
2.求数列的和注意方法的选取:关键是看数列的通项公式; 求和过程中注意分类讨论思想的运用;
三.下列习题你必须掌握:
1.各项都是正数的等比数列{ }的公比q≠1,且
}的公比q≠1,且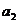 ,
, ,
,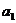 成等差数列,则
成等差数列,则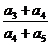 的值为( )
的值为( )
A.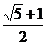 B.
B.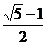 C.
C.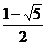 D.
D.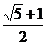 或
或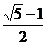
解析: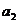 ,
, ,
,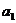 成等差数列得到了关于首项和公差的关系,带入到所求式子可以减少未知数。
成等差数列得到了关于首项和公差的关系,带入到所求式子可以减少未知数。
2.设等差数列{an}的前n项的和为Sn,若a1>0,S4=S8,则当Sn取得最大值时,n的值为
A.5 B.
3.设数列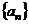 是等差数列,且
是等差数列,且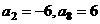 ,
,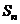 是数列
是数列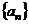 的前
的前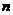 项和,则( )
项和,则( )
A、 B、
B、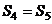 C、
C、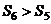 D、
D、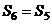
解析:2,3两道题都要用函数的思想来解决,注意到等差数列的前n项和是关于n的二次函数,找出对称轴。
4.若一等数列的前7项的和为48, 前14项的和为72, 则它的前21项的和为 ( )
A. 96 B.
5.已知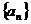 为等比数列,
为等比数列, ,
,
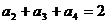 ,那么,
,那么,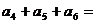 。
。
6.求下列数列的前n项和:
(1)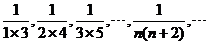 ;
;
(2)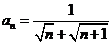 ;
;
(3)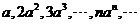 ;
;
7.已知数列{an}为等差数列,公差d≠0,其中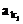 ,
,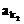 ,…,
,…,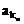 恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn。
恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com