
假期复习第十三天―――平面向量
一.这几个概念你掌握了吗?请回顾一遍:
1.向量的加法与减法、实数与向量的积、向量的数量积及其运算法则。
2.向量共线和垂直的充要条件是什么?
3.运用正弦定理、余弦定理、三角形面积公式及关系式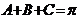 ,解决三角形中的计算和证明问题。
,解决三角形中的计算和证明问题。
4.线段的定比分点坐标公式和中点坐标公式,
5.平移公式,会用平移公式化简函数式或求平移后的函数解析式.
二.特别要注意下列方法:
1.数量积的性质: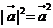 ,
,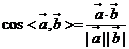 ;
;
2.向量垂直的充要条件:符号语言: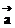 ⊥
⊥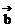

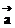 ?
?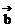 =0
=0
坐标语言:设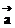 =(x1,y1),
=(x1,y1), 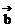 =(x2,y2),则
=(x2,y2),则
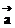 ⊥
⊥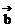
 x1x2+y1y2=0
x1x2+y1y2=0
3.两个向量平行的充要条件
符号语言:若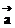 ∥
∥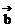 ,
,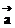 ≠
≠ ,则
,则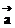 =λ
=λ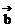
坐标语言为:设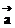 =(x1,y1),
=(x1,y1),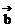 =(x2,y2),则
=(x2,y2),则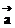 ∥
∥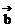
 (x1,y1)=λ(x2,y2),即
(x1,y1)=λ(x2,y2),即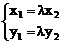 ,或x1y2-x2y1=0
,或x1y2-x2y1=0
三.下列习题你必须掌握:
1.已知向量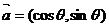 ,向量
,向量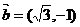 则
则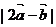 的最大值,最小值分别是( )
的最大值,最小值分别是( )
A.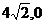 B.
B.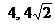 C.16,0 D.4,0
C.16,0 D.4,0
2. △ABC中,2cosB?sinC=sinA,则此三角形是:
A.直角 B、等腰 C、等边 D、以上均有可能
3. 已知向量 不超过5,则k的取值范围是
不超过5,则k的取值范围是
4.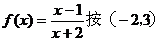 平移后得到:____________.
平移后得到:____________.
5.已知向量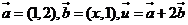 ,
,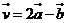 ,且
,且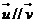 ,求实数
,求实数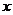 的值。
的值。
6.已知 ,
,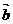 ,
,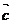 是平面内的三个向量,其中
是平面内的三个向量,其中 =(1,2).(1)若|
=(1,2).(1)若|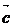 |
|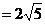 ,且
,且 ,求
,求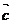 的坐标;
的坐标;
(2)若|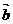 |=
|=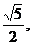
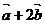 与
与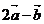 垂直,求
垂直,求 ,
,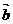 的夹角.
的夹角.
7.已知向量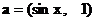 ,
, 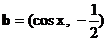 .
.
(1) 当 时, 求
时, 求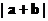 的值;
的值;
(2) 求函数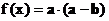 的值域.
的值域.
8.A,B,C为△ABC的三内角,且其对边分别为a,b,c.若 =(-cos,sin),
=(-cos,sin),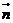 =(cos,sin),且
=(cos,sin),且 ?
?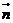 =.
=.
(1)求A;
(2)若a=2,三角形面积S=,求b+c的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com