
2009年安庆九中高三文科数学(五)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数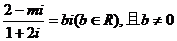 ,则
,则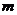 的值是( )
的值是( )
A.-1
B.
2.已知命题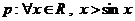 ,则
,则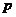 的否定形式为( )
的否定形式为( )
A.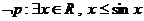 B.
B.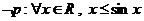
C. 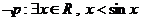 D.
D.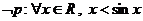
3.若关于x的方程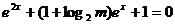
 ,则m的取值范围是( )
,则m的取值范围是( )
A.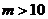 B.
B.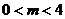 C.
C.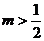 D.
D.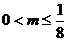
4.在面积为S的三角形ABC的边AB上任取一点P,则三角形的面积大于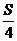 的概率是( )
的概率是( )
A.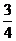 B.
B.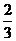 C.
C.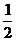 D.
D.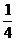
5.函数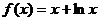 的零点所在的区间为( )
的零点所在的区间为( )
A.(-1,0) B.(0,1) C.(1,2) D.(1,e)
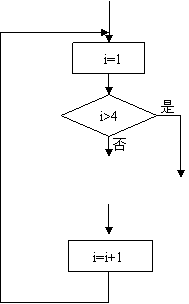
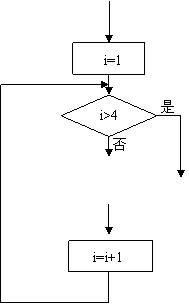
6.如图(1)是某循环的一部分,若改为图(2),则运行过程中出现( )
 |
|||
 |
|||
(1) (2)
A.不循环 B.循环次数增加
C.循环次数减少,且只循环有限次 D.无限循环
7.在某篮球比赛中,甲、乙两名运动员都参加了11场比赛,他们每场比赛得分的情况用茎叶图表示如图所示,则这两名运动员比赛得分的中位数分别是( )
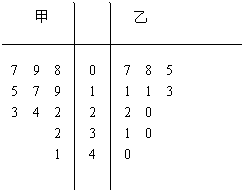 |
A.13,19 B.19,13
C.20,18 D.18,20
8.已知在平面直角坐标系中O(0,0),A(3,0),B(0,3),动点P在直线上,满足: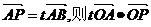 最大值为( )
最大值为( )
A.13
B.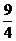 D.
D.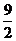
9.过椭圆左焦点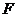 作直线交椭圆于
作直线交椭圆于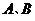 两点,若
两点,若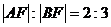 ,且直线与长轴的夹角为
,且直线与长轴的夹角为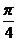 ,则椭圆的离心率为 ( )
( )
,则椭圆的离心率为 ( )
( )
A、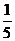 B、
B、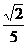 C、
C、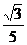 D、
D、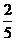
10.曲线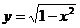 上存在不同的三点到点(2,0)的距离构成等比数列,则以下不可能成为公比的数是( )
上存在不同的三点到点(2,0)的距离构成等比数列,则以下不可能成为公比的数是( )
A.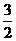 B.
B.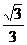 C.
C.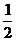 D.
D.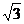
11.设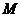 是非空实数集,若
是非空实数集,若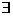
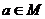 ,使得对于
,使得对于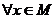 ,都有
,都有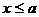
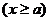 ,
,
则称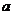 是
是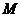 的最大(小)值,若
的最大(小)值,若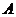 是一个不含零的非空实数集,且m是
是一个不含零的非空实数集,且m是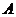 的最大值,则( )
的最大值,则( )
A. 当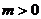 时,
时,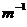 是集合
是集合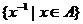 的最小值;
的最小值;
B. 当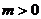 时,
时,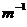 是集合
是集合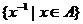 的最大值;
的最大值;
C. 当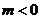 时,
时,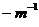 是集合
是集合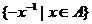 的最小值;
的最小值;
D. 当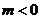 时,
时,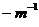 是集合
是集合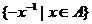 的最大值;
的最大值;
12.多面体表面上三个或三个以上平面的公共点称为多面体的顶点,用一个平面截一个n棱柱,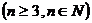 截去一个三棱锥,剩下的多面体顶点的数目是
截去一个三棱锥,剩下的多面体顶点的数目是
 ( )
( )
A、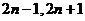 B、
B、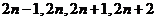
C、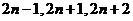 D、
D、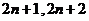
二.填空题:(本大题共4个小题,每小题4分,共16分,把答案填在题中的横线上)
13.某同学5次上学途中所花时间(单位:分钟)分别为x,y,10,11,9。已知这组数据的平均数为10,方差为2,则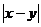 的值为
的值为
14.已知函数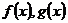 满足
满足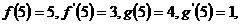 则函数
则函数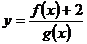 的图像在
的图像在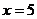 处的切线方程为
处的切线方程为
15.研究问题:“已知关于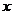 的不等式
的不等式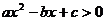 的解集为
的解集为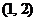 ,解关于
,解关于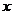 的不等式
的不等式
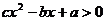 ”,有如下解法:
”,有如下解法:
解:由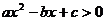
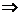
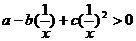 ,令
,令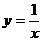 ,则
,则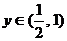 ,
,
所以不等式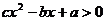 的解集为
的解集为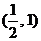 .
.
参考上述解法,已知关于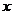 的不等式
的不等式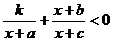 的解集为
的解集为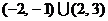 ,则
,则
关于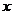 的不等式
的不等式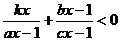 的解集为 .
的解集为 .
16.运用物理中矢量运算及向量坐标表示与运算,我们知道:
(1)若两点等分单位圆时,有相应关系为: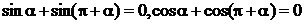
(2)四点等分单位圆时,有相应关系为:
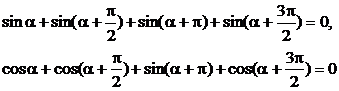
由此可以推知三等分单位圆时的相应关系为:
三.解答题(本大题共6个小题,共74分。解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究顺序,研究函数f(x)= +的性质,并在此基础上,作出其在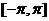 的草图
的草图
18.(本小题满分12分)
一个多面体的直观图及三视图如图所示(其中E、F分别是PB、AD的中点).
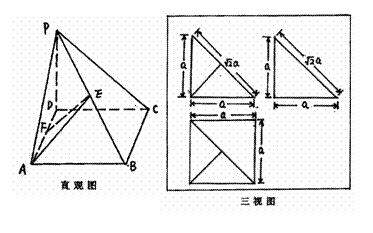 (Ⅰ)求证:EF⊥平面PBC;
(Ⅰ)求证:EF⊥平面PBC;
(Ⅱ)求三棱锥B―AEF的体积。
19.(本小题满分12分)
已知函数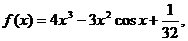 其中
其中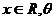 为参数,且
为参数,且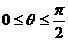 。
。
(1)当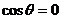 时,判断函数
时,判断函数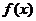 是否有极值;
是否有极值;
(2)要使得函数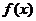 的极小值大零,求参数
的极小值大零,求参数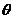 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数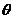 ,函数
,函数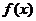 在区间
在区间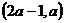 内都是增函数,求实数
内都是增函数,求实数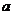 的取值范围。
的取值范围。
20.(本小题满分12分)
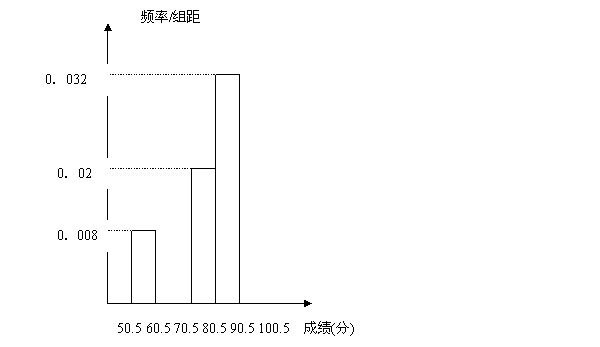
为了让学生了解环保知识,增强环保一是,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成并有局部污损的频率分布直方图和频率分布表,解答下列问题:
(1)填充频率分布表的表格(将答案直接填在表格中)
(2)补全频率分布直方图
(3)若成绩在75.5―85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
分组
频数
频率
50.5―60.5
4
0.08
60.5―70.5
0.16
70.5―80.5
10
80.5―90.5
16
0.32
90.5―100.5
合计
50

21.(本小题满分12分)
设数列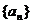 的各项都为正数,且对任意
的各项都为正数,且对任意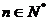 ,都有
,都有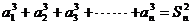 ,其中
,其中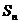 为数列
为数列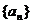 的前
的前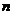 项和。
项和。
(1)求证: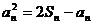 ;
;
(2)求数列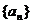 的通项公式;
的通项公式;
(3)设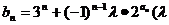 为非零整数,
为非零整数,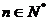 ),试确定
),试确定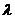 的值,使得对任意
的值,使得对任意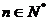 ,都有
,都有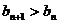 成立。
成立。
22.(本小题满分14分)
以O为原点, 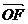 所在直线为
所在直线为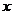 轴,建立直角坐标系,设
轴,建立直角坐标系,设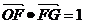 ,点F的坐标为(t,0),
,点F的坐标为(t,0),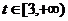 ,点G的坐标为
,点G的坐标为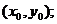
(1)求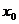 关于t的函数
关于t的函数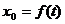 的表达式,判断函数
的表达式,判断函数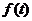 的单调性,并证明你的判断;
的单调性,并证明你的判断;
(2)设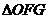 的面积
的面积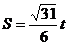 ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当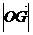 取最小值时椭圆方程。
取最小值时椭圆方程。
(3)在(2)的条件下,若点P的坐标为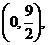 C,D是椭圆上的两点,且
C,D是椭圆上的两点,且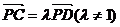 ,求实数
,求实数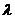 的取值范围。
的取值范围。
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
A
B
D
B
C
B
C
D
B
1.提示:
 ,故选C。
,故选C。
2.提示:“任意的”否定为“存在”;“>”的否定为“ ”,故选A
”,故选A
3.提示: 又
又 ,所以
,所以 ,故选D。
,故选D。
4.提示:在AB上取点D,使得 ,则点P只能在AD内运动,则
,则点P只能在AD内运动,则 ,
,
5.提示:排除法选B。
6.提示:由图(1)改为图(2)后每次循环时 的值都为1,因此运行过程出现无限循环,故选D
的值都为1,因此运行过程出现无限循环,故选D
7.提示:由茎叶图的定义,甲得分为7,8,9,15,19,23,24,26,32,41。共11个数,19是中位数,乙得分为5,7,11,11,13,20,22,30,31,40。共11个数,13是中位数。
故选B。
8.提示: 得
得 所以
所以 ,故选C。
,故选C。
 9.提示:由
9.提示:由 及
及 得
得
 如图
如图
过A作 于M,则
于M,则



 得
得 .
.
故选B.
10.提示:不妨设点(2,0)与曲线 上不同的三的点距离为分别
上不同的三的点距离为分别 ,它们组成的等比数列的公比为
,它们组成的等比数列的公比为 若令
若令 ,显然
,显然 ,又
,又 所以
所以 ,
, 不能取到
不能取到 。故选B。
。故选B。
11.提示:使用特值法:取集合 当
当 可以排除A、B;
可以排除A、B;
取集合 ,当
,当 可以排除C;故选D;
可以排除C;故选D;
12.提示:n棱柱有 个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)
个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)






2在图4,图6所示的情形,还剩 个顶点;
个顶点;
在图5的情形,还剩 个顶点;
个顶点;
在图2,图3的情形,还剩 个顶点;
个顶点;
在图1的情形,还剩下 个顶点.故选B.
个顶点.故选B.
二、填空题:
13.4
提示:
 由(1),(2)得
由(1),(2)得 或
或 ,所以
,所以 。
。
14.
提示:斜率 ,切点
,切点 ,所以切线方程为:
,所以切线方程为:
15.
提示:当 时,不等式无解,当
时,不等式无解,当 时,不等式变为
时,不等式变为 ,
,
由题意得 或
或 ,所以,
,所以, 或
或
16.
三、解答题:
17.解:① ∵ ∴
∴ 的定义域为R;
的定义域为R;
② ∵ ,
,
∴ 为偶函数;
为偶函数;
③ ∵ , ∴
, ∴ 是周期为
是周期为 的周期函数;
的周期函数;
④ 当 时,
时, =
= ,
,
∴当 时
时 单调递减;当
单调递减;当 时,
时,
 =
= ,
,
 单调递增;又∵
单调递增;又∵ 是周期为
是周期为 的偶函数,∴
的偶函数,∴ 在
在 上单调递增,在
上单调递增,在 上单调递减(
上单调递减( );
);
⑤ ∵当 时
时 ;
;
当 时
时 .∴
.∴ 的值域为
的值域为 ;
;
⑥由以上性质可得: 在
在 上的图象如图所示:
上的图象如图所示:

18.解:(Ⅰ)取PC的中点G,连结EG,GD,则
由(Ⅰ)知FD⊥平面PDC, 面PDC,所以FD⊥DG。
面PDC,所以FD⊥DG。
所以四边形FEGD为矩形,因为G为等腰Rt△RPD斜边PC的中点,
所以DG⊥PC,
|