．三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数为偶函数， 且
（1）求的值；
（2）若为三角形的一个内角，求满足的的值.

．三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤.

16. (本题满分12分)

已知函数为偶函数， 且

（1）求的值；

（2）若为三角形的一个内角，求满足的的值.

（本题满分12分）
对甲、乙两种商品的重量的误差进行抽查，测得数据如下(单位：)：
甲：13  15  14  14  9  14  21  9   10  11
乙：10  14  9  12  15  14  11  19  22  16
（1）画出样本数据的茎叶图，并指出甲，乙两种商品重量误差的中位数；
（2）计算甲种商品重量误差的样本方差；
（3）现从重量误差不低于15的乙种商品中随机抽取两件，求重量误差为19的商品被抽
中的概率。

（本题满分12分）为了了解某年级1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.

（1）将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；

（2）求调查中随机抽取了多少个学生的百米成绩；

（3）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.

（本题满分12分）某学校共有教职工900人,分成三个批次进行继续教育培训，在三个批次中男、女教职工人数如下表所示. 已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 .

（1）求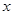的值；

（2）现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中抽取教职工多少名？

（3）已知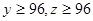，求第三批次中女教职工比男教职工多的概率.