
题目列表(包括答案和解析)
4. 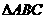 中,
中,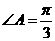 ,
,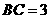 ,
,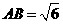 ,则
,则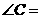
A. 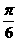 B.
B.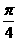 C.
C.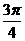 D.
D.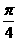 或
或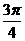
3. 椭圆 的焦点在
的焦点在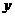 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则 的值为( )
的值为( )
A.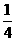 B.
B.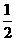 C. 2 D.4
C. 2 D.4
2. 设全集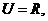 且
且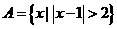 ,
,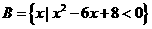 ,则
,则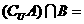
A.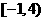 B.
B.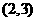 C.
C.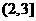 D.
D.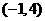
1. 已知复数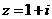 ,则
,则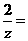
A. 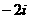 B.
B.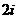 C.
C. 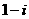 D.
D. 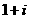
21. (本题满分14分)
解:(Ⅰ) 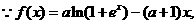
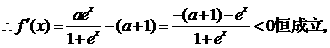 …………………………
…………………………
所以函数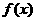 在
在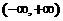 上是单调减函数.
上是单调减函数. …………………………4分
…………………………4分
(Ⅱ)
证明:据题意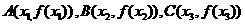 且x1<x2<x3,
且x1<x2<x3,
由(Ⅰ)知f
(x1)>f (x2)>f (x3), x2=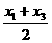 …………………………6分
…………………………6分
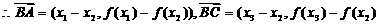
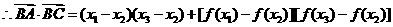 …………………8分
…………………8分
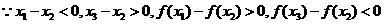
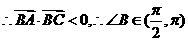
即⊿ 是钝角三角形……………………………………..9分
是钝角三角形……………………………………..9分
(Ⅲ)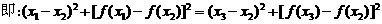 假设⊿
假设⊿ 为等腰三角形,则只能是
为等腰三角形,则只能是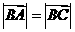
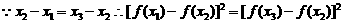 即
即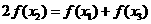
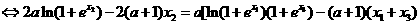
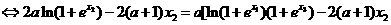
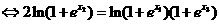
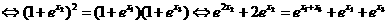
 ①
…………………………………………..12分
①
…………………………………………..12分
而事实上, 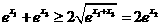 ②
②
由于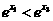 ,故(2)式等号不成立.这与
,故(2)式等号不成立.这与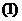 式矛盾. 所以⊿
式矛盾. 所以⊿ 不可能为等腰三角形..14分
不可能为等腰三角形..14分
20. (本题满分14分)
.解: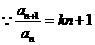
故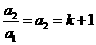 ,.……………………………………1分
,.……………………………………1分
又因为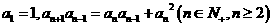
则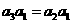
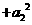 ,即
,即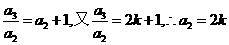 .………………………3分
.………………………3分
所以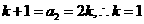 , ……………………………………4
, ……………………………………4
(2)
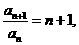
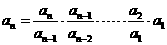 =
=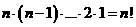 ……………………………………6
……………………………………6
因为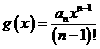 =
=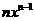
所以,当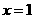 时,
时,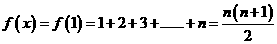 ……………………………7
……………………………7
当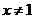 时,
时,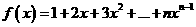 ……….(1)
……….(1)
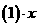 得
得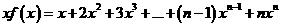 ……(2)
……(2)
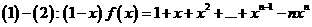
=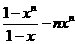
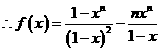 ……………………………9
……………………………9
综上所述: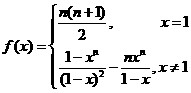 ……………………………10
……………………………10
(3)因为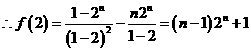
又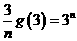 ,易验证当
,易验证当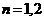 ,3时不等式不成立; ……………………………11
,3时不等式不成立; ……………………………11
假设 ,不等式成立,即
,不等式成立,即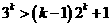
两边乘以3得: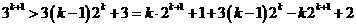
又因为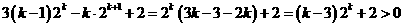
所以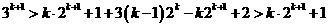
即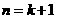 时不等式成立.故不等式恒成立. ……………………………14
时不等式成立.故不等式恒成立. ……………………………14
19. (本题满分14分)
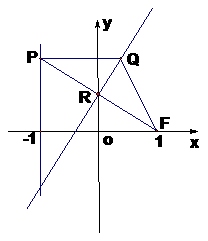 解:(Ⅰ)依题意知,直线
解:(Ⅰ)依题意知,直线 的方程为:
的方程为: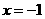 .点
.点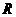 是线段
是线段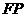 的中点,且
的中点,且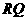 ⊥
⊥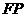 ,∴
,∴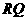 是线段
是线段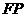 的垂直平分线.…………………….2分
的垂直平分线.…………………….2分
∴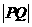 是点
是点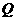 到直线
到直线 的距离.
的距离.
∵点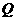 在线段
在线段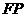 的垂直平分线,∴
的垂直平分线,∴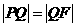 .…………4分
.…………4分
故动点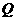 的轨迹
的轨迹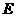 是以
是以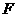 为焦点,
为焦点, 为准线的抛物线,其方程为:
为准线的抛物线,其方程为: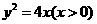 .…………………………………………………….7分
.…………………………………………………….7分
(Ⅱ) 设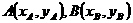 ,
,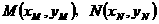 ,直线AB的方程为
,直线AB的方程为
…………………………………………………….8分
则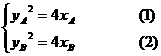
(1)-(2)得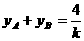 ,即
,即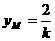 ,……………………………………9分
,……………………………………9分
代入方程 ,解得
,解得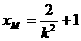 .
.
所以点M的坐标为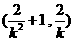 .……………………………………10分
.……………………………………10分
同理可得: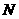 的坐标为
的坐标为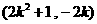 .
.
直线 的斜率为
的斜率为 ,方程为
,方程为
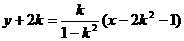 ,整理得
,整理得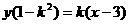 ,………………12分
,………………12分
显然,不论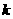 为何值,
为何值,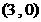 均满足方程,
均满足方程,
所以直线 恒过定点
恒过定点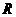
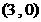 .………………14
.………………14
18.(本题满分12分)
证(Ⅰ)因为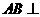 侧面
侧面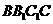 ,故
,故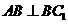
在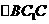 中,
中,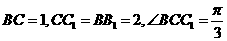 由余弦定理有
由余弦定理有
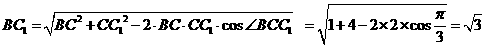
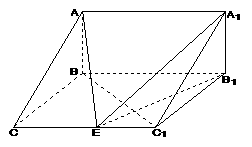 故有
故有 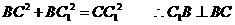
而 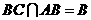 且
且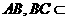 平面
平面


(Ⅱ)由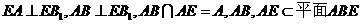
从而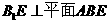 且
且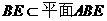 故
故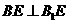
不妨设 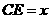 ,则
,则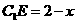 ,则
,则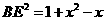
又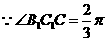 则
则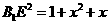
在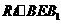 中有
中有 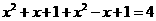 从而
从而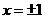 (舍负)
(舍负)
故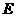 为
为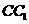 的中点时,
的中点时,
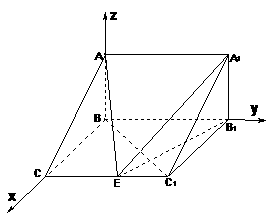 法二:以
法二:以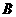 为原点
为原点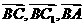 为
为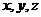 轴,设
轴,设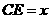 ,则
,则 由
由 得
得 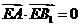 即
即
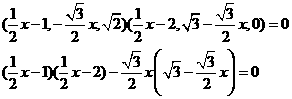
化简整理得 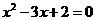
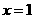 或
或 
当 时
时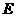 与
与 重合不满足题意
重合不满足题意
当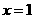 时
时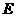 为
为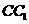 的中点
的中点
故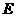 为
为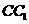 的中点使
的中点使
(Ⅲ)取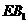 的中点
的中点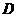 ,
,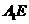 的中点
的中点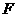 ,
,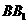 的中点
的中点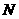 ,
, 的中点
的中点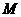
连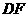 则
则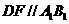 ,连
,连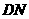 则
则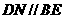 ,连
,连 则
则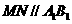
连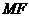 则
则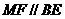 ,且
,且 为矩形,
为矩形,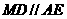
又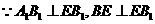 故
故 为所求二面角的平面角
为所求二面角的平面角
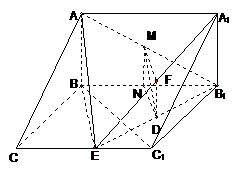 在
在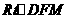 中,
中,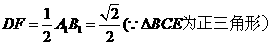

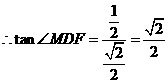
法二:由已知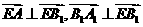 , 所以二面角
, 所以二面角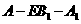 的平面角
的平面角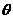 的大小为向量
的大小为向量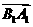 与
与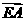 的夹角
的夹角
因为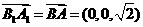
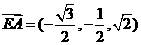
故 
.
17.(本题满分12分)
解:(Ⅰ)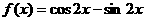 =
=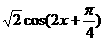 …………………….4分
…………………….4分
故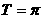 …………………………………………………5分
…………………………………………………5分
(Ⅱ)令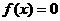 ,
,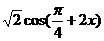 =0,又
=0,又
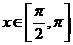 …… ………….7分
…… ………….7分
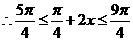
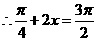 …………………………………………9分
…………………………………………9分
故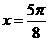 函数
函数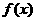 的零点是
的零点是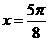 …………….
12分
…………….
12分
16. (本题满分12分)
(本题满分12分)
(Ⅰ)因为各组的频率和等于1,故第四组的频率:
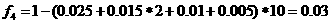 ……2分
……2分
直方图如右所示……………………………….4分
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 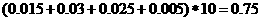
所以,抽样学生成绩的合格率是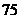 %......................................6分
%......................................6分
利用组中值估算抽样学生的平均分
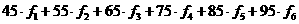 ………………….8分
………………….8分
=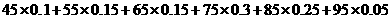
=71
估计这次考试的平均分是71分………………………………………….9分
(Ⅲ)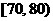 ,
,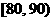 ,
,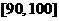 ”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
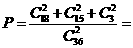
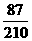 ……………………………………………………12分
……………………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com