
题目列表(包括答案和解析)
1、已知函数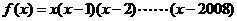 ,则
,则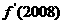 =
。2008!
=
。2008!
19、已知函数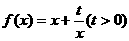 和点
和点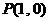 ,过点
,过点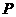 作曲线
作曲线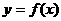 的两条切线
的两条切线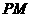 、
、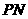 ,切点分别为
,切点分别为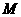 、
、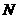 .
.
(Ⅰ)设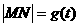 ,试求函数
,试求函数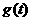 的表达式;
的表达式;
(Ⅱ)是否存在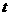 ,使得
,使得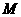 、
、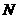 与
与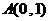 三点共线.若存在,求出
三点共线.若存在,求出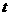 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数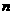 ,在区间
,在区间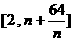 内总存在
内总存在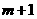 个实数
个实数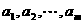 ,
,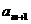 ,使得不等式
,使得不等式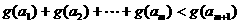 成立,求
成立,求 的最大值.
的最大值.
18、设函数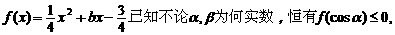
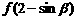
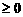 .对于正项数列
.对于正项数列 ,其前
,其前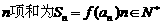
(1)求实数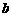 (2)求数列
(2)求数列 的通项公式
的通项公式
(3)若 大小,并说明理由。
大小,并说明理由。
17、将函数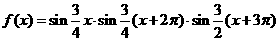 在区间
在区间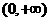 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列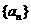 ,
,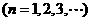 .
.
(Ⅰ)求数列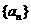 的通项公式;
的通项公式;
(Ⅱ)设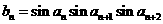 ,求证:
,求证: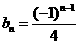 ,
,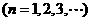 .
.
16、设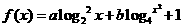 ,
,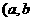 为常数).当
为常数).当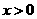 时,
时,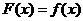 ,且
,且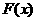 为
为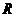 上的奇函数.
上的奇函数.
(Ⅰ)若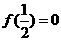 ,且
,且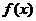 的最小值为
的最小值为 ,求
,求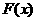 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,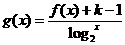 在
在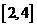 上是单调函数,求
上是单调函数,求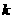 的取值范围.
的取值范围.
15、若数列{an}的通项公式an=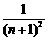 ,记
,记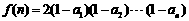 ,试通过计算
,试通过计算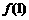 ,
,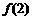 ,
,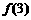 的值,推测出
的值,推测出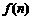 = .
= .
14、设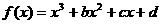 ,又
,又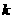 是一个常数,已知当
是一个常数,已知当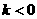 或
或 时,
时,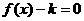 只有一个实根;当
只有一个实根;当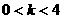 时,
时,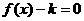 有三个相异实根,现给下列命题:
有三个相异实根,现给下列命题:
(1)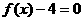 与
与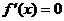 有一个相同的实根;
有一个相同的实根;
(2)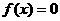 与
与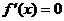 有一个相同的实根;
有一个相同的实根;
(3)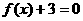 的任一实根大于
的任一实根大于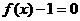 的任一实根;
的任一实根;
(4)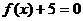 的任一实根小于
的任一实根小于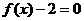 的任一实根。其中所有正确命题是
的任一实根。其中所有正确命题是
13、对于各数互不相等的正数数组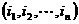 (
(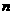 是不小于
是不小于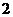 的正整数),如果在
的正整数),如果在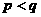 时有
时有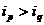 ,则称
,则称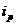 与
与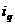 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”.若各数互不相等的正数数组
是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”.若各数互不相等的正数数组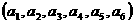 的“逆序数”是2,则
的“逆序数”是2,则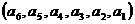 的“逆序数”是
.
的“逆序数”是
.
12、数列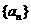 中,如果存在非零常数
中,如果存在非零常数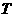 ,使得
,使得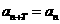 对于任意的非零自然数
对于任意的非零自然数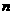 均成立,那么就称数列
均成立,那么就称数列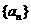 为周期数列,其中
为周期数列,其中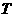 叫做数列
叫做数列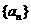 的周期。已知数列
的周期。已知数列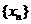 满足
满足
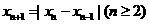 ,如果
,如果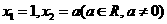 ,当数列
,当数列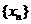 的周期最小时,求该数列前2007项和是 ____________.
的周期最小时,求该数列前2007项和是 ____________.
11、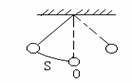 如图,单摆从某点开始来回摆动,离开平衡位置O的距离S厘米和时间
如图,单摆从某点开始来回摆动,离开平衡位置O的距离S厘米和时间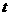 秒的函数关系为:
秒的函数关系为: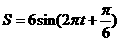 ,那么单摆来回摆动一次所需的时间为
秒.
,那么单摆来回摆动一次所需的时间为
秒.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com