练习册

  • 练习册
  • 试题
    已知的定义域为区间[-1.1]. 【查看更多】

     

    题目列表(包括答案和解析)

    已知的定义域为区间[－1，1]。

       （1）求函数的解析式；

       （2）判断的单调性；

       （3）若方程的取值范围。

    查看答案和解析>>

    已知定义域为R的函数在区间内是增函数。

    （1）求实数的取值范围；

    （2）若的极小值为－2，求实数的值。

    查看答案和解析>>

    已知定义域为R的函数f(x)在区间(－∞，5)上单调递减，对任意实数t，都有f(5+t)=f(5－t)，试判断f(－1)、f(9)、f(13)的大小。

    查看答案和解析>>

    已知定义域为R的函数f(x)在区间(－∞，5)上单调递减，对任意实数t，都有f(5+t)=f(5－t)，试判断f(－1)、f(9)、f(13)的大小。

    查看答案和解析>>

    已知＝(2asin2x，a)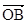，＝(－1,2sinxcosx＋1)，O为坐标原点，a≠0，设f(x)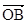＝·＋b，b>a。

    (1)若a>0，写出函数y＝f(x)的单调递增区间；

    (2)若函数y＝f(x)的定义域为[，π]，值域为[2,5]，求实数a与b的值。

     

    查看答案和解析>>

     

    一、选择题

    1．D   2．A   3．C   4．B   5．D   6．A   7．A   8．A   9．B   10．D

    2,4,6

    11．40    12．   13．3    14．①②③④

    三、解答题

    15．解：（1）设数列

    由题意得：

    解得：

       （2）依题

    ，

    为首项为2，公比为4的等比数列

       （2）由

    16．解：（1），

       （2）由

     

    17．解法1：

    设轮船的速度为x千米/小时（x>0），

    则航行1公里的时间为小时。

    依题意，设与速度有关的每小时燃料费用为，

    答：轮船的速度应定为每小时20公里，行驶1公里所需的费用总和最小。

    解法2：

    设轮船的速度为x千米/小时（x>0），

    则航行1公里的时间为小时，

    依题意，设与速度有关的每小时燃料费用为

    元，

    且当时等号成立。

    答：轮船的速度应定为每小时20公里，行驶1公里所需的费用总和最小。

    18．证明：（1）连结AC、BD交于点O，再连结MO ，

       （2）

       

    19．解：（1），半径为1依题设直线，

        由圆C与l相切得：

       （2）设线段AB中点为

        代入即为所求的轨迹方程。

       （3）

       

    20．解：（1）

       （2）

       （3）由（2）知

    在[－1，1]内有解

     

     

     


    同步练习册答案