
题目列表(包括答案和解析)
在下列函数中,既是区间![]() 上的增函数,又是以π为周期的偶函数的是( )
上的增函数,又是以π为周期的偶函数的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 ,使
,使 ;
; 既有最大值和最小值,又是偶函数;
既有最大值和最小值,又是偶函数; 的最小正周期为π.
的最小正周期为π.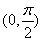 ,使sinx+cosx=
,使sinx+cosx=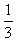 ;
;  既有最大值和最小值,又是偶函数;
既有最大值和最小值,又是偶函数;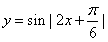 的最小正周期为π;
的最小正周期为π;| π |
| 2 |
| 1 |
| 3 |
| π |
| 2 |
| π |
| 6 |
一、选择题
1.D 2.A 3.C 4.B 5.D 6.A 7.A 8.A 9.B 10.D
|