
题目列表(包括答案和解析)
如图,在正四面体S—ABC中,E为SA的中点,F为DABC的
中心,则异面直线EF与AB所成的角是
A.30° B.45°
C.60° D.90°

如图,在正四面体S―ABC中,E为SA的中点,F为DABC的中心,则异面直线EF与AB所成的角是
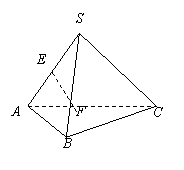
A.30° B.45° C.60° D.90°
如图,在正四面体S―ABC中,E为SA的中点,F为DABC的中心,则异面直线EF与AB所成的角是

A.30° B.45° C.60° D.90°
 如图,在正四面体S—ABC中,E为SA的中点,F为DABC的中心,则异面直线EF与AB所成的角是 。
如图,在正四面体S—ABC中,E为SA的中点,F为DABC的中心,则异面直线EF与AB所成的角是 。
 如图,在正四面体S—ABC中,E为SA的中点,F为DABC的中心,则异面直线EF与AB所成的角是 。
如图,在正四面体S—ABC中,E为SA的中点,F为DABC的中心,则异面直线EF与AB所成的角是 。
一、选择题:
|