题目列表(包括答案和解析)
（本题满分12分）
某工厂生产一种产品的成本费由三部分组成：① 职工工资固定支出
元；② 原材料费每件40元；③ 电力与机器保养等费用为每件
元，其中
是该厂生产这种产品的总件数.
（1）把每件产品的成本费P(x)（元）表示成产品件数的函数，并求每件产品的最低成本费；
（2）如果该厂生产的这种产品的数量不超过
件，且产品能全部销售．根据市场调查：每件产品的销售价
与产品件数有如下关系：
，试问生产多少件产品，总利润最高？（总利润=总销售额—总的成本）
(本小题满分12分）
某工厂生产一种精密仪器， 产品是否合格需先后经过两道相互独立的工序检查，且当第一道工序检查合格后才能进入到第二道工序，经长期检测发现，该仪器第一道工序检查合格的概率为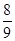
，第二道工序检查合格的概率为
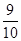，已知该厂每月生产3台这种仪器.
（1）求生产一台合格仪器的概率;
（2）用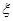
表示每月生产合格仪器的台数，求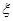的分布列和数学期望;
（3）若生产一台合格仪器可盈利10万元，不合格要亏损3万元，求该厂每月的期望盈利额.
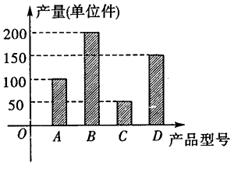（3）从A、C型号的产品中随机的抽取3件，用
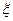表示抽取A种型号的产品件数，求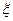的分布列和数学期望。（本题满分12分）某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元.该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但出厂单价不能低于51元.
（1）当一次订购量为多少个时，零件的实际出厂单价恰降为51元？
（2）设一次订购量为
个时，零件的实际出厂单价为P元，写出函数的表达式；
（3）当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个时，利润又是多少元？（工厂售出一个零件的利润=实际出厂单价-成本）
(本小题满分12分)
某工厂生产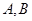
两种元件，其质量按测试指标划分为：大于或等于7．5为正品，小于7．5为次品．现从一批产品中随机抽取这两种元件各5件进行检测，检测结果记录如下：
|
|
7 |
7 |
7．5 |
9 |
9．5 |
|
|
6 |
|
8．5 |
8．5 |
|
由于表格被污损，数据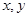
看不清，统计员只记得
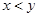，且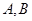两种元件的检测数据的平均值相等，方差也相等．
（Ⅰ）求表格中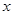
与
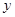的值；
（Ⅱ）若从被检测的5件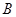
种元件中任取2件，求2件都为正品的概率．
一．选择题
1~10 BADDA BCBCD
二．填空题
11．2
12．
13．
14．8 15．45
三．解答题
16．解：因为
，所以
………………………………（1分）
由
得
，解得
………………………………（3分）
因为
，故集合
应分为
和
两种情况
（1）时，
…………………………………（6分）
（2）时，
……………………………………（8分）
所以得
…………………………………………………（9分）
若
真
假，则
…………………………………………………………（10分）
若假真，则
……………………………………………………………（11分）
故实数
的取值范围为或………………………………………（12分）
17．解：（1）由1
的解集有且只有一个元素知
或
………………………………………（2分）
当
时，函数
在
上递增，此时不满足条件2
综上可知
…………………………………………（3分）
……………………………………（6分）
（2）由条件可知
……………………………………（7分）
当
时，令
或
所以
或
……………………………………………………………（9分）
又
时，也有
……………………………（11分）
综上可得数列
的变号数为3……………………………………………（12分）
18．解：（1）当
时，
………………………（1分）
当
时，
……………………（2分）
由
，知
又是周期为4的函数，所以
当
时
…………………………（4分）
当
时
…………………………（6分）
故当
时，函数
的解析式为
………………………………（7分）
（2）当
时，由
，得
或
或
解上述两个不等式组得
…………………………………………（10分）
故
的解集为
…………………（12分）
19．解：（1）当
时，
，
……………………（2分）
当
时，
，
综上，日盈利额
（万元）与日产量
（万件）的函数关系为：
…………………………………………………………（4分）
（2）由（1）知，当时，每天的盈利额为0……………………………（6分）
当时，
当且仅当
时取等号
所以
当
时，
，此时……………………………（8分）
当
时，由
知
函数在
上递增，
，此时
……（10分）
综上，若，则当日产量为3万件时，可获得最大利润
若，则当日产量为
万件时，可获得最大利润…………（12分）
20．解：（1）将点
代入
得
因为直线
，所以
……………………………………（3分）
（2）
，
当
为偶数时，
为奇数，
……………（5分）
当为奇数时，为偶数，
（舍去）
综上，存在唯一的
符合条件…………………………………………………（7分）
（3）证明不等式
即证明
成立，下面用数学归纳法证明
1当
时，不等式左边=
，原不等式显然成立………………………（8分）
2假设
时，原不等式成立，即
当
时
=
，即时，原不等式也成立 ………………（11分）
根据12所得，原不等式对一切自然数都成立 ……………………………（13分）
21．解：（1）由
得
……………………（1分）
又的定义域为
，所以
当
时，
当
时，
，为减函数
当
时，
，为增函数………………………（5分）
所以当时，的单调递增区间为
单调递减区间为
…………………（6分）
（2）由（1）知当
时，
，递增无极值………（7分）
所以在
处有极值，故且
因为
且
，所以在
上单调
当为增区间时，
恒成立，则有
………………………………………（9分）
当为减区间时，恒成立，则有
无解 ……………………（13分）
由上讨论得实数的取值范围为
…………………………（14分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com