
题目列表(包括答案和解析)
已知函数![]() (其中
(其中![]() ) ,
) ,
点![]() 从左到右依次是函数
从左到右依次是函数![]() 图象上三点,且
图象上三点,且![]() .
.
(Ⅰ) 证明: 函数![]() 在
在![]() 上是减函数;
上是减函数;
(Ⅱ) 求证:⊿![]() 是钝角三角形;
是钝角三角形;
(Ⅲ) 试问,⊿![]() 能否是等腰三角形?若能,求⊿
能否是等腰三角形?若能,求⊿![]() 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.
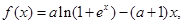 (其中
(其中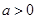 ) ,点
) ,点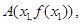
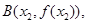
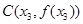 从左到右依次是函数
从左到右依次是函数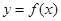 图象上三点,且
图象上三点,且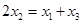 .
.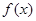 在
在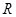 上是减函数;
上是减函数;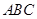 是钝角三角形;
是钝角三角形;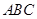 能否是等腰三角形?若能,求⊿
能否是等腰三角形?若能,求⊿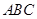 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.已知函数![]() (其中
(其中![]() ) ,
) ,
点![]() 从左到右依次是函数
从左到右依次是函数![]() 图象上三点,且
图象上三点,且![]() .
.
(Ⅰ) 证明: 函数![]() 在
在![]() 上是减函数;
上是减函数;
(Ⅱ) 求证:⊿![]() 是钝角三角形;
是钝角三角形;
(Ⅲ) 试问,⊿![]() 能否是等腰三角形?若能,求⊿
能否是等腰三角形?若能,求⊿![]() 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.
有向线段 的
的
 等分点从左到右依次为
等分点从左到右依次为 ,
, ,…,
,…, ,记
,记
 ,则
,则
 的
的
 等分点从左到右依次为
等分点从左到右依次为 ,
, ,…,
,…, ,记
,记
 ,则
,则
一、选择题:
1.D 2.D 3.D 4.C 5.A 6.D 7.B 8.C 9.B 10.B 11.D 12.D
二、填空题:
13、.files/image351.gif)
.files/image353.jpg) 14、
14、.files/image355.gif) 15、对任意
15、对任意.files/image160.gif) 使
使.files/image358.gif) 16、2 17、
16、2 17、.files/image360.gif)
18、.files/image362.gif) 19、
19、.files/image364.gif) 20、8 21、
20、8 21、.files/image366.gif) 22、40 23、
22、40 23、.files/image368.gif)
24、4 25、.files/image370.gif) 26、
26、.files/image372.gif)
三、解答题:
27解:(1)由.files/image374.gif) ,得
,得
.files/image376.gif) ,
,
.files/image378.gif) ,
,
.files/image380.gif) ,
, .files/image382.gif) ,
,
于是.files/image384.gif) ,
,
.files/image386.gif) ,
,
∴.files/image388.gif) ,即
,即.files/image268.gif)
.files/image391.gif) .
.
(2)∵.files/image266.gif) 角是一个三角形的最小内角,∴0<
角是一个三角形的最小内角,∴0<.files/image266.gif) ≤
≤.files/image394.gif) ,
,.files/image396.gif) ,
,
设.files/image398.gif) ,则
,则.files/image398.gif) ≥
≥.files/image401.gif) (当且仅当
(当且仅当.files/image403.gif) 时取=),
时取=),
故函数.files/image268.gif) 的值域为
的值域为.files/image405.gif) .
.
28证明:(1).files/image407.gif) 同理,
同理,.files/image409.gif)
又∵.files/image411.gif) ∴
∴.files/image413.gif) 平面
平面.files/image415.gif) .
.
(2)由(1)有.files/image413.gif) 平面
平面.files/image415.gif)
又∵.files/image417.gif) 平面
平面.files/image281.gif) , ∴平面
, ∴平面.files/image279.gif) 平面
平面.files/image281.gif) .
.
(3)连接AG并延长交CD于H,连接EH,则.files/image421.gif) ,
,
在AE上取点F使得.files/image423.gif) ,则
,则.files/image425.gif) ,易知GF
,易知GF.files/image286.gif) 平面CDE.
平面CDE.
29解:(1).files/image428.gif) ,
,
.files/image430.gif) ,
,.files/image432.gif) ,
,
∴.files/image434.gif) 。
。
(2)∵.files/image436.gif) ,
,
∴当且仅当.files/image438.gif) ,即
,即.files/image440.gif) 时,
时,.files/image256.gif) 有最大值。
有最大值。
∵.files/image442.gif) ,∴取
,∴取.files/image444.gif) 时,
时,.files/image446.gif) (元),
(元),
此时,.files/image448.gif) (元)。答:第3天或第17天销售收入最高,
(元)。答:第3天或第17天销售收入最高,
此时应将单价.files/image179.gif) 定为7元为好
定为7元为好
30解:(1)设M.files/image450.gif)
∵点M在MA上∴.files/image452.gif) ①
①
同理可得.files/image454.gif) ②
②
由①②知AB的方程为.files/image456.gif)
易知右焦点F(.files/image458.gif) )满足③式,故AB恒过椭圆C的右焦点F(
)满足③式,故AB恒过椭圆C的右焦点F(.files/image458.gif) )
)
(2)把AB的方程.files/image460.gif)
∴.files/image462.gif)
又M到AB的距离.files/image464.gif)
∴△ABM的面积.files/image466.gif)
31解:(Ⅰ)
.files/image468.gif)
.files/image470.gif)
所以函数.files/image126.gif) 在
在.files/image473.gif) 上是单调减函数.
上是单调减函数..files/image475.gif)
(Ⅱ) 证明:据题意.files/image317.gif) 且x1<x2<x3,
且x1<x2<x3,
由(Ⅰ)知f (x1)>f (x2)>f (x3), x2=.files/image477.gif)
.files/image479.gif)
.files/image481.gif)
.files/image483.gif)
.files/image485.gif)
即ㄓ.files/image281.gif) 是钝角三角形
是钝角三角形
(Ⅲ)假设ㄓ.files/image281.gif) 为等腰三角形,则只能是
为等腰三角形,则只能是.files/image488.gif)
.files/image490.gif)
即.files/image492.gif)
.files/image494.gif)
.files/image496.gif)
.files/image498.gif)
.files/image500.gif)
.files/image502.gif) ①
①
而事实上, .files/image504.gif) ②
②
由于.files/image506.gif) ,故(2)式等号不成立.这与
,故(2)式等号不成立.这与.files/image508.gif) 式矛盾. 所以ㄓ
式矛盾. 所以ㄓ.files/image281.gif) 不可能为等腰三角形.
不可能为等腰三角形.
32解:(Ⅰ).files/image511.gif)
.files/image513.gif)
故数列.files/image329.gif) 为等比数列,公比为3.
为等比数列,公比为3.
(Ⅱ).files/image515.gif)
.files/image517.gif)
所以数列.files/image519.gif) 是以
是以.files/image521.gif) 为首项,公差为 loga3的等差数列.
为首项,公差为 loga3的等差数列.
又.files/image523.gif)
.files/image525.gif)
又.files/image527.gif) =1+3
=1+3.files/image529.gif) ,且
,且.files/image343.gif)
.files/image532.gif)
.files/image534.gif)
(Ⅲ).files/image536.gif)
.files/image538.gif)
.files/image540.gif)
假设第.files/image542.gif) 项后有
项后有.files/image349.gif)
.files/image545.gif) 即第
即第.files/image542.gif) 项后
项后.files/image547.gif) ,于是原命题等价于
,于是原命题等价于
.files/image549.gif)
.files/image551.gif)
.files/image553.gif) 故数列
故数列.files/image329.gif) 从
从.files/image555.gif) 项起满足
项起满足.files/image349.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com