
题目列表(包括答案和解析)
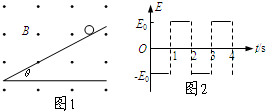 在如图1所示的区域里,存在垂直指相纸外的磁感应强度为B=2πm/q的匀强磁场;在竖直方向存在随时间交替变化的如图2所示的匀强电场,场强大小E0=mg/q,设竖直向上为正方向.一倾角为θ且足够长的光滑绝缘斜面竖直放置其中.斜面上一带正电小球(质量为m,电量为q)从t=0时刻开始沿斜面无初速滑下.设第一秒内小球不会脱离斜面,求:
在如图1所示的区域里,存在垂直指相纸外的磁感应强度为B=2πm/q的匀强磁场;在竖直方向存在随时间交替变化的如图2所示的匀强电场,场强大小E0=mg/q,设竖直向上为正方向.一倾角为θ且足够长的光滑绝缘斜面竖直放置其中.斜面上一带正电小球(质量为m,电量为q)从t=0时刻开始沿斜面无初速滑下.设第一秒内小球不会脱离斜面,求:
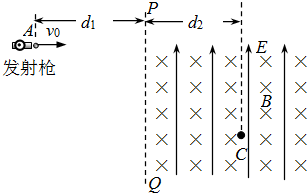 如图所示,竖直平面内,直线PQ右侧足够大的区域内存在竖直向上的匀强电场和垂直于纸面向里的匀强磁场,左侧到直线距离为d1=0.4m的A处有一个发射枪.发射枪将质量m=0.01kg,带电量q=+0.01C的小球以某一初速度v0水平射出,当竖直位移为d1/2时,小球进入电磁场区域,随后恰能做匀速圆周运动,且圆周最低点C(图中运动的轨迹未画出)到直线PQ的距离为d2=0.8m.不计空气阻力,g取10m/s2.试求:
如图所示,竖直平面内,直线PQ右侧足够大的区域内存在竖直向上的匀强电场和垂直于纸面向里的匀强磁场,左侧到直线距离为d1=0.4m的A处有一个发射枪.发射枪将质量m=0.01kg,带电量q=+0.01C的小球以某一初速度v0水平射出,当竖直位移为d1/2时,小球进入电磁场区域,随后恰能做匀速圆周运动,且圆周最低点C(图中运动的轨迹未画出)到直线PQ的距离为d2=0.8m.不计空气阻力,g取10m/s2.试求:如图所示,竖直平面内,直线PQ右侧足够大的区域内存在竖直向上的匀强电场和垂直于纸面向里的匀强磁场,左侧到直线距离为d1=0.4m的A处有一个发射枪。发射枪将质量m=0.01kg,带电量q= +0.01C的小球以某一初速度v0水平射出,当竖直位移为d1/2时,小球进入电磁场区域,随后恰能做匀速圆周运动,且圆周最低点C(图中运动的轨迹未画出)到直线PQ的距离为d2=0.8m.不计空气阻力,g取10m/s2。试求:
(1)小球水平射出的初速度v0和电场强度E;
(2)小球从水平射出至运动到C点的时间t;
(3)若只将PQ右侧的电场强度变为原来的一半,小球进入电磁场区域后做曲线运动,轨迹的最低点为C′(图中未画出),则求:最低点C′离发射点A的竖直方向距离d及运动过程中的最小速度v。
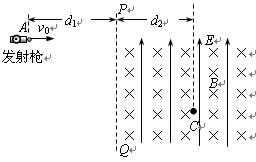
.如图(甲)所示,在xoy平面内有足够大的匀强电场,电场方向竖直向上,电场强度E=40N/C.在y轴左侧平面内有足够大的瞬时磁场,磁感应强度B1随时间t变化规律如图(乙)所示,15π s后磁场消失,选定磁场垂直向里为正方向.在y轴右侧平面内还有方向垂直纸面向外的恒定的匀强磁场,分布在一个半径为r=0.3m的圆形区域(图中未画出),且圆的左侧与y轴相切,磁感应强度B2=0.8T.t=0时刻,一质量m=8×10-4kg、电荷量q=2×10-4C的微粒从x轴上xP=-0.8m处的P点以速度v=0.12m/s向x轴正方向入射.(计算结果保留二位有效数字)

(1)求微粒在第二像限运动过程中离y轴、x轴的最大距离;
(2)若微粒穿过y轴右侧圆形磁场时,速度方向的偏转角度最大,求此圆形磁场的圆心坐标(x、y);
(3)若微粒以最大偏转角穿过磁场后, 击中x轴上的M点,求微粒从射入圆形磁场到击中M点的运动时间t。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com